小学数学理思型课堂构建的内涵、原则与策略
2024-06-28徐世凤
徐世凤


[摘要] “理思”既是教学之术,也是教学之道;既是数学之境,也是数学之魂。构建小学数学理思型课堂,教师需要明确理思型课堂的基本内涵,即“探究数学原理、学会数学思考”,并遵循其任务探究性原则、学生主体性原则、教师精导性原则,真正实现课堂教学方式的变革;通过创设真实性问题情境、跳跃式问题情境、抽象型问题情境等实施策略,引领学生学会数学思考、思辨、思想。
[关键词] 小学数学;理思型课堂;课堂构建
《义务教育数学课程标准(2022年版)》指出,数学为人们提供了一种认识与探究现实世界的观察方式、理解与解释现实世界的思考方式、描述与交流现实世界的表达方式。小学数学教学中,教师要改变单一讲授式教学方式,注重课堂教学方式的变革,构建一种以核心素养为目标导向的理思型课堂,培养学生适应未来发展的必备品格和关键能力,真正促进“三会”核心素养落地。构建小学数学理思型课堂,需要明确理思型课堂的基本内涵,遵循任务探究性原则、学生主体性原则、教师精导性原则,并创设真实性问题情境、跳跃式问题情境、抽象型问题情境,让学生学会数学思考、思辨、思想。
一、小学数学理思型课堂构建的内涵
经查询,“理思”的释义是“思辨力;合理的思考”。其出处之一是《宋书·王僧绰传》:“﹝僧绰﹞好学有理思,练悉朝典。”在本文,“理思”是“理”和“思”的结合,“理”是理性层面的,指数学中的道理、算理、原理等;“思”是实践层面的,指思考、思辨、思想等。小学数学理思型课堂是一种以“探究数学原理、学会数学思考”为核心内容的课堂,强调以“理”促“思”,以“思”明“理”,最终达成“理思并进”。小学数学理思型课堂的构建,旨在带领学生在鲜活的数学课堂中学会用数学的眼光观察现实世界,学会用数学的思维思考现实世界,学会用数学的语言表达现实世界。
二、小学数学理思型课堂构建的原则
其一,任务探究性原则。小数数学理思型课堂是以任务探究为主的课堂,无论是计算课,还是解决问题课,甚至是概念课等,都应围绕相应教学内容的核心问题设计探究任务,一节课最多只能设计三个探究任务,探究的任务不能太开放,也不能太保守,探究的任务要有聚焦点,更要有留白处。
其二,学生主体性原则。在理思型课堂中,学生围绕探究任务,先独立思考,后小组交流,再全班汇报。全班汇报时,学生在前,教师在后,学生汇报完,凭借“我的发言完毕,你们同意吗?还有补充或疑问的吗?”等语言支架来传递“话筒”,凸显自己的课堂主体地位。
其三,教师精导性原则。在理思型课堂中,教师“看似不在,却一直都在”。教师犹如一位“主持人”,把整个课堂的舞台交给学生,在学生展示汇报的过程中,时刻关注学生之间的交流,一旦发现“离题”就及时介入,并在关键处点拨,在小结处提炼,发挥精导的作用。
三、小学数学理思型课堂构建的策略
1.创设真实性问题情境,引发学生学会理性思考
理性思考不仅能够帮助我们正确看待问题,而且能够提高我们的数学分析和判断能力。只有在充分理性思考的基础上,我们才能对真实性问题进行深入分析和思考,理解问题的本质,找到解决问题的方法,提高思维能力。比如,人教版六年级上册“百分数的再认识”一课教学,教师创设“2023年杭州亚运会男篮比赛”真实问题情境,出示中国男篮主力王哲林的罚球命中数据(见表1),思考:(1)你认为哪个罚球命中率更能代表他的水平?为什么?(2)请你预测他下一场比赛的罚球命中率,并说明理由。
百分数从数的领域进入统计量范畴,它不仅可以表示一个数或者两个数据的倍数关系,而且还可以表示一组随机数据。学生经历用百分数表达随机数据的过程,感悟百分数的统计意义,并根据百分数做出合理、理性的预测。在此基础上,针对王哲林20%的罚球命中率,教师出示网络上的部分负面评论,引发学生思考:对于这些批评的声音,你有什么想说的?学生经过理性思考,能辩证地分析问题,在大数据时代保持理性的思维。
2.创设跳跃式问题情境,启发学生进行明理思辨
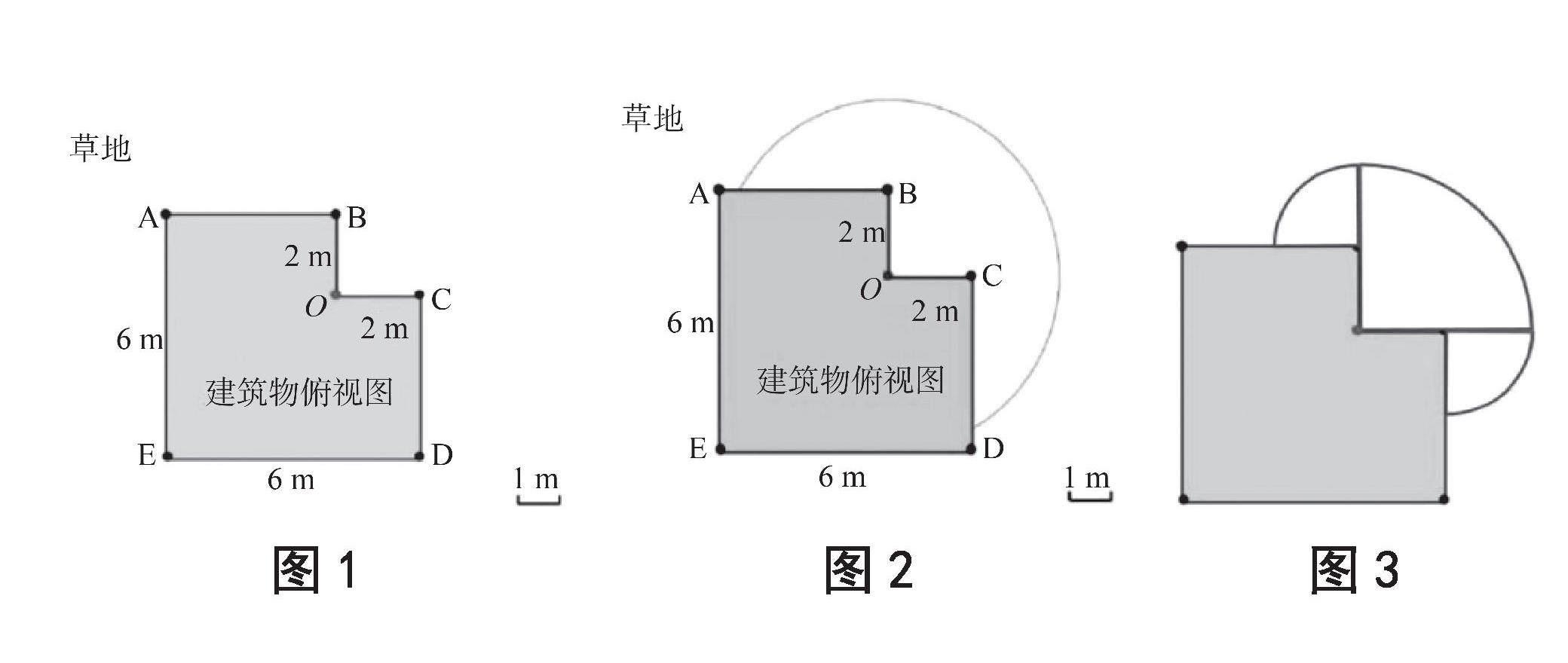
思辨是数学教学的价值取向之一,要真正发展学生数学核心素养,必须以培养学生的数学思维为抓手。在理思型课堂构建中,首先需要根据数学思维的发展特点,创设富有挑战性的跳跃式问题,引导学生进行有效思辨,在思辨中学会明理。比如,六年级上册“圆的面积”拓展课教学——羊能吃多大面积的草地,首先创设如下问题情境:一座建筑物墙角O点处拴了一只羊,拴羊的绳子长1米,这只羊能吃到多大面积的草地?(见图1)由于绳子长比2米短,绳子不用拐弯,学生不难发现:羊可以吃一个半径为1米的四分之一圆面积的草地。
接着,出示第一次跳跃式问题:如图1所示,一座建筑物墙角O点处拴了一只羊,拴羊的绳子长4米,这只羊能吃到多大面积的草地?此时,学生出现两种不同想法:第一种想法是羊以绳子长4米为半径,不受墙角拐弯的影响,直接吃出一个圆的一部分草地(见图2),第二种想法是羊首先会以绳子长4米为半径吃出一个四分之一圆的草地,当羊的绳子遇到墙角B、C点时,绳子长会发生变化,绳子长被墙角截短成2米,接着再吃出两个以2米为半径的四分之一圆的草地(见图3)。两种想法引发学生深度思辨,学生通过对比图2和图3,在思辨中明晰羊真正能吃到的草地面积。
随后,教师出示第二次跳跃式问题:当绳子长超过几米时,解决问题的思路会再一次发生变化呢?为什么?尝试把你的想法写下来。一个拐点带给学生不同层次的思辨,学生通过观察、比较、想象、思辨等数学活动,感受到数学思维的魅力所在。
3.创设抽象型问题情境,带领学生感悟数学思想
在小学数学理思型课堂中,教师应适时地借助教学内容,帮助学生在自主探究中逐步感悟数学思想方法。数形结合是一种非常重要的数学思想,利用图形来直观地解释一些比较抽象的数学原理与事实,可以使抽象的问题变得更直观。小学生思维的抽象程度还不够高,在解决抽象型问题时,需要借助直观模型来帮助理解。比如,利用长方形模型来教学分数乘法的算理,利用线段图来帮助学生理解分数除法的算理,利用面积模型来解释两位数乘两位数的算理、乘法分配律等。
又如,六年级上册“数与形”课堂上的例2,出现了解决++++++…的求和问题。“无限”的
概念非常抽象,学生不易理解,有的学生会说最终的结果无限接近于1,但永远不可能等于1。事实上,该例体现了“极限”的核心思想。教学中,教师可以引导学生画一个圆或一个正方形,甚至是一条线段,再根据分数的意义表示出这些加数(见图4)。这样,学生利用分数意义的直观模型,能直观地看到最终的结果是1,从而理解“无限”的抽象概念。并且,学生在利用数学结合解决问题的过程中也积累了基本的活动经验,体会到数形结合、归纳推理,以及极限等基本的数学思想。
总而言之,“理思”既是教学之术,也是教学之道;既是数学之境,也是数学之魂。小学数学理思型课堂的构建,教师应遵循儿童的思维特点,以数学的本质内容为核心,引领学生在探究数学原理的过程中感悟数学思想方法,在寻理、明理、悟理中发展数学理性思维,并逐步从理性思维走向理性精神。
