基于GA-RBF网络的混合气体红外光谱定量检测
2024-06-24吴广谱
摘 要:混合气体组分的定量分析在各个领域都尤为重要,传统的气体成分检测方法一般是采用电化学法和气相色谱法,此类方法检测效率低下、精度不够,且无法做到实时测量。为解决这一问题,本文由HITRAN光谱数据库获取100组混合气体样本数据集,以样本中CO2和H2O组分为例,利用RBF网络分别进行定量识别。结果得知,两种气体在训练集和测试集的预测浓度值与实际浓度值偏差均较大, RBF网络无法准确的预测出混合气体组分的浓度。为改进该问题,考虑到模型参数对RBF网络回归预测精度的影响,本文在此基础上提出一种GA优化RBF网络的混合气体组分浓度检测方法。通过引入GA优化RBF网络模型参数,获取最优参数组,再将优化模型用于混合气体组分定量识别。并与RBF网络预测算法在同一数据集上对比论证,探讨模型改进效果。实验结果表明,相较于单独使用RBF网络,改进后的GA-RBF模型在混合气体组分定量识别问题中,表现更为优异。
关键词: 红外光谱;RBF神经网络;遗传算法;浓度检测
1 概述
混合气体组分浓度检测一直是研究热点,它在各大领域都发挥着重要作用,如机动车尾气排放、工业废气污染排放检测等。随着我国经济的快速增长,人们在对生活品质关注的同时也对生存环境提出了更高的要求,因工业废气、汽车尾气等有毒气体的排放造成了严重的环境污染。尤其是在垃圾焚烧行业,尾气中含大量CO2、H2O等气体,烟气湿度高达70%,且监测的气体组分复杂,以往投入火电厂[1]使用的常温仪表在使用过程中由于尾气的特性极易造成腐蚀问题,后期维护量大,系统使用寿命短暂。因此提出一种能够准确检测混合气体组分浓度的方法具有较大价值。
基于红外光谱技术的混合气体浓度检测问题是红外光谱领域的重要问题。随着计算机技术的飞速发展,利用机器学习算法与红外光谱技术相融合[2]用于混合气体组分浓度检测逐渐成为研究热点。大数据时代的开启,使得从繁杂的数据库中高效提取出有用数据成为可能。这些新技术和理论促进了我国原有检测技术的发展,同时大幅度提高了检测精度。
传统气体检测方法会受到外界环境,如温度、压强等因素的影响,所测准确度并不稳定,需与其他方法相结合,才能达到检测目标。现阶段提高传感器检测精度的方法主要有人工神经网络[3] (ANN)法和支持向量机[4] (SVM)等机器学习算法。王玮[5]用BP网络检测出了CO、SO2、NO的单一气体的浓度,平均误差达到3.59%。太惠玲等[6]人采用3层BP神经网络检测出CO和H2浓度,CO和H2平均相对误差分别是0.74%和1.75%。Lei Zhang等[7]人对比了SMIMO和MMISO两种算法在多层感知网络优化上的应用,得出MMISO在气体浓度估计上误差更小。
以上方法对单一气体的浓度检测精度较高,但对多组分混合气体的浓度检测精度往往达不到要求。本文以此出发,提出一种改进RBF网络的混合气体组分定量分析方法。首先通过GA优化RBF网络模型参数,获取最优参数组,再将优化模型用于混合气体组分定量识别。并与传统RBF网络预测算法在同一数据集上对比论证。
2 混合气体浓度检测的RBF网络模型
2.1 RBF网络训练算法
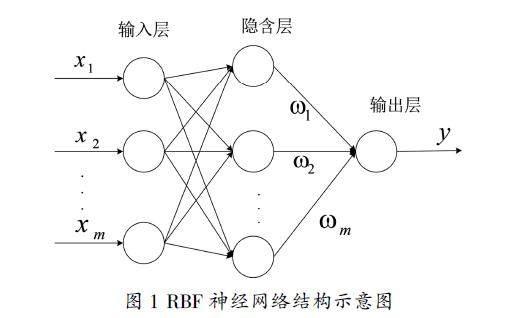
RBF网络是一种包含三层网络结构的前向型网络,网络结构如图1所示[8]。
RBF网络基本思想是:用径向基函数作为隐单元的“基”,构成隐层空间。隐层对输入向量进行变换,将低维空间的模式变换到高维空间,使低维空间线性不可分的问题在高维空间内线性可分。
实现步骤如下:
2.1.1 确立径向基函数中心点
设训练集样本输入矩阵和输出矩阵分别如下式(2.1)和(2.2)所示:
其中,表示第个训练样本的第个输入变量;表示第个训练样本的第个输出变量;为输入变量的维;为输出变量的维;为训练集样本总数。
2.1.2 确定隐含层神经元阈值
令个隐含层神经元对应的阈值为式(2.3)
其中,,为径向基函数的扩展速度。
2.1.3 确定隐含层与输出层间权值和阈值
当隐含层神经元的径向基函数中心及阈值确定后,隐含层神经元的输出便可以
由式(2.4)计算:
其中,为第个训练样本向量。并记。
设隐含层和输出层间的连接权值为式(2.5)
其中,表示第个隐含层神经元与第个输出层神经元之间的连接权值。
设个输出层神经元的阈值为下式(2.6)
由RBF神经网络结构可得式(2.7)
其中
求解线性方程组(2.7),即可得到隐含层和输出层之间的权值W和阈值b2,如式(2.8)所示
本节所采用的混合气体光谱数据集由HITRAN光谱数据库获得,共100组。将数据集随机划分为训练集和测试集。其中,训练集包含80组数据,测试集包含20组。
通过上述理论分析,本节将利用RBF神经网络对包含CO2和 H2O样本的混合气体红外光谱数据集进行训练和回归预测,并结合平均相对误差及预测值与真实值的拟合相关系数作为模型评价指标,对预测结果进行分析。
2.2 两种气体浓度预测实验验证与分析
2.2.1 RBF网络对CO2气体的定量分析
将随机选择的80组数据作为训练集样本建立回归分析模型。在测试集上验证模型的预测效果,训练集样本CO2的模型预测浓度值与实际浓度值对比如图2所示。
由图2可以看出,利用训练集样本建立的RBF模型对训练集数据做预测时,效果不理想,模型预测浓度值无法较好的拟合真实值。对数据误差进行计算,结果可得训练集平均相对误差为0.237,实际浓度值与预测浓度值的拟合相关系数为0.8067。由两个模型评价参数可知,RBF网络对CO2训练集浓度的预测效果较差。
将训练后的RBF模型应用于测试集,测试集的实际浓度和预测浓度对比如图3。
由图3可以看出,将模型用于测试集的预测,其预测浓度值与实际浓度值偏差同样比较大。对数据误差进行计算,测试集平均相对误差为0.215,实际值与预测值的拟合相关系数为0.7986。
由以上分析可知RBF算法在测试集上的回归分析能力效果较差,RBF网络无法准确地预测CO2组分浓度。故此模型不能用于混合气体中CO2组分浓度的定量分析。
2.2.2 RBF网络对H2O气体的定量分析
为使实验仿真结果更具说服力,在同一混合气体数据集下,将RBF网络用于H2O训练集和测试集样本的浓度回归预测,所得实验结果如下图4所示。
计算数据误差,结果可得训练集平均相对误差为0.599,相关系数为0.7432。预测浓度与实际浓度偏差较大,预测效果不理想。将训练的模型应用于测试集,测试集的实际浓度和预测浓度对比如下图5所示。
图5 H2O测试集实际浓度和预测浓度对比
根据图5结果可以得知,将模型用于测试集的预测,其预测浓度值与实际浓度值拟合效果较差。计算数据误差可知,测试集平均相对误差为0.431,预测浓度值与真实浓度值拟合相关系数为0.7352。分析可知RBF算法对H2O的回归预测能力较差,RBF算法无法准确地预测H2O组分浓度。模型不适用于混合气体中H2O组分浓度的定量分析。
RBF网络对两种气体组分在训练集和测试集上预测的模型评价参数如下表所示:
由表1 RBF模型预测结果分析可知,RBF神经网络在混合气体组分定量识别问题中呈现出的结果并不理想,RBF网络无法准确预测出混合气体组分浓度。考虑到RBF网络模型参数对识别精度的影响。为解决这一问题,本文在RBF网络的基础上提出一种改进算法,即遗传算法(GA)优化RBF网络的混合气体组分浓度预测方法。
3 GA优化RBF网络用于混合气体组分定量分析
3.1 GA基本原理
遗传算法(GA)是根据自然界生物体的进化规律而提出的,是一种模拟自然进化过程进而搜索最优解的方法[9]。该算法通过数学求解方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的选择、交叉和变异等的过程。通过种群一代代的不断进化,最终收敛到“最适应环境”的个体,从而求得问题最优解。
遗传算法(GA)是模型参数优化的常用方法。该算法的基本优化过程是采用基于适应度函数的选择、交叉和变异等操作,获取网络模型的最优参数组,以此来提高网络的预测精度。论文采用GA对RBF神经网络的主要参数不断调节和优化,其中主要参数包括有中心值c、宽度σ和连接权值w等。再以对输出响应值有影响的若干个特征因子作为输入神经元,输出响应值作为输出神经元,对GA-RBF神经网络模型进行训练和测试。并将模型应用在与上述RBF预测算法同一样本数据集上对比论证,观察GA-RBF模型的预测效果。
3.2 GA优化RBF实现过程
GA优化RBF网络具体实现流程如下图6所示:
从图6中可以看出遗传算法优化RBF神经网络主要包括三个模块:确定网络结构、遗传算法优化模型参数以及RBF网络预测。首先根据输入和输出参数的个数确定基本的网络结构,确立遗传算法中个体长度值。再通过比较不同宽度种群下的适应度值及遗传算子的变异概率,对遗传操作方式不断地改进。最后对优化所得最优个体分别赋与RBF神经网络的初始权值、中心值及阈值,训练完成后对网络进行预测分析。
优化的基本要素包括种群初始化、计算适应度函数、选择、交叉与变异操作。
3.2.1对种群进行初始化
通过GA对种群中的个体进行编码,编码后的个体相当于一个实数串,它包括四个部分,分别是输入层与隐含层的连接权值、隐含层阈值、隐含层与输出层的连接权值以及输出层阈值。
3.2.2计算适应度函数
首先依据个体获取RBF网络的初始权值及阈值,通过训练后的RBF网络在训练集上预测适应度值,适应度值计算方法如公式(3.1)所示:
上式中,为第个输出点的预测值,为第个输出点的期望值,为输出节点的个数,为系数。
3.2.3选择操作
依据预测的适应度值大小执行选择操作,若令个体被选中的概率为,则其计算方法如公式(3.2)所示:
上式中,,为种群个体的适应度值,为种群中所包含的个体数。
3.2.4交叉操作
个体的编码方式采用的是实数编码,因此交叉操作采用实数交叉。如第个染色体与第个染色体在位进行交叉操作,则有:
上式中,为[0,1]之间的随机数。
3.2.5变异操作
以种群个体的第个染色体为例,变异操作可表示为:
上式中,为的上限,为的下限。;是随机数,是当前的寻优次数,为设定的迭代次数,为[0,1]之间的随机数。
3.3 优化模型在样本集中的验证分析
本节以包含CO2、H2O组分的混合气体数据集作为研究对象,对两种气体单独建模进行浓度的定量分析。其中,混合气体中CO2浓度范围为0.08%~48.83%,H2O浓度范围为0.03%~39.58%。
选择与上述RBF预测方法相同的100组混合气体光谱样本数据集,其中80组样本作为训练集,融合遗传算法建立神经网络优化模型,观察优化模型在训练集上的回归预测效果。选取其余20组样本作为测试集,利用训练后的模型在测试集上回归预测,验证优化模型在测试集上的预测精度。将优化模型预测结果与单独使用RBF神经网络对比分析,比较两者的预测值与真实值拟合相关系数和平均相对误差,评价两种模型在混合气体组分定量分析中的优劣。
建立神经网络模型需合理优化选取初始权值、中心值及阈值,本节利用GA实现参数寻优过程,其具体步骤如上图6所示。
具体优化步骤为:
(1) 选取与上述RBF预测相同的100组实验数据用作样本集,其中80组为训练样本集,其余20组用为测试样本集。
(2) 确定RBF网络结构。本节同时对含两组分的混合气体定量识别,因此可设置RBF网络结构为2-7-1模式,即输入层节点数目为2,隐含层节点数目为7和输出层节点数目为1。
(3) 初始化网络获取初始权值、阈值。
(4) 初始化GA各个参数。本次实验选择种群的规模为80;选取空间[10,100];迭代次数设定为400;交叉概率设定为0.3,设定范围[0,1];变异概率取0.1。根据所设参数,初始化种群初始位置及寻优速度。
(5) 设定适应度函数是训练数据预测误差的绝对值之和。
(6) 对种群初始化。
(7) 迭代寻优求解出最优初始权值、中心值及阈值。根据式(3.2)、(3.3)与(3.4)对个体执行选择、交叉与变异操作,通过对个体适应度值的横向及纵向对比获取当前最优个体。
(8) 判断寻优结果是否符合结束条件,若不符合,则跳到第六步继续执行此过程。
将通过GA优化获得的最优个体赋与RBF网络,进而对训练样本集训练并以此构建神经网络回归模型,再在此基础上对测试集验证分析模型预测结果。
对于两种气体分析模型的参数优化过程,设定种群数量80,GA优化迭代次数为400,交叉概率0.3,变异概率0.1。按照图6的优化流程逐步进行,若以横轴为迭代次数,纵轴为适应度值,可得到如下图7所示的GA优化过程中最优个体适应度值变化规律曲线。
3.3.1 GA-RBF对CO2气体的定量分析
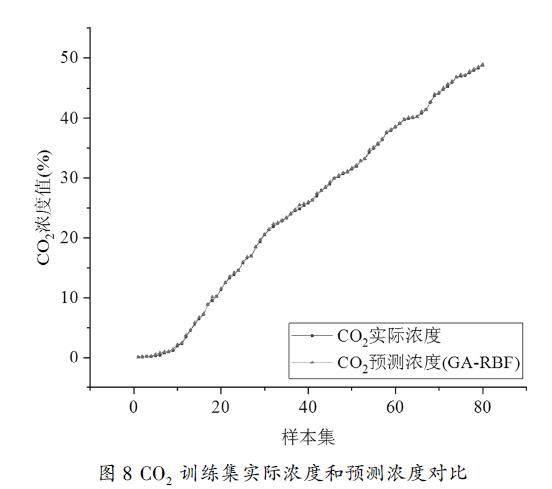
对于筛选出的80组样本数据,将其作为训练集样本训练,构建优化回归模型。分别在训练集和测试集上对模型的回归效果验证分析。其中,模型在训练集样本上预测浓度值和实际浓度值对比结果如下图8所示。
由图8可看出利用训练样本集建立的模型对训练集本身做预测时,预测效果较好,预测浓度值能够很好的拟合真实浓度值。对数据误差进行计算,结果可得训练集平均相对误差为0.041,预测浓度值与实际值浓度的拟合相关系数为0.9671。分析可知GA-RBF模型相较于单独使用RBF,具有较好的回归预测能力,可以准确预测样本中的CO2浓度。
将训练后的模型用于测试集验证,测试集样本的实际浓度值和预测浓度值对比如下图9所示。
观察图9可知,GA-RBF模型在测试集预测效果较好,其预测浓度值与实际浓度拟合程度较高。可推断GA-RBF模型可以用于混合气体组分CO2浓度的定量分析。 计算可得测试集平均相对误差为0.024,预测值与真实值的拟合相关系数为0.9576。分析可知GA-RBF模型相较于单独使用RBF,具有较好的回归预测能力,可以精确预测样本中CO2的浓度信息。
3.3.2 GA-RBF对H2O气体的定量分析
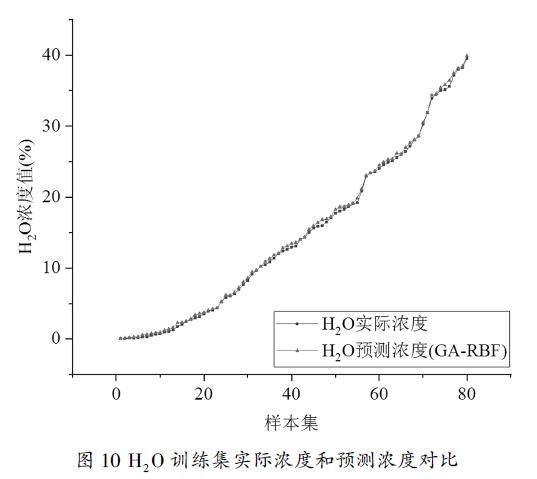
对于随机选择的80组样本数据,将其作为训练样本训练,构建优化回归分析模型。分别论证模型在训练集和测试集上的预测效果。训练集样本中模型预测浓度值和实际浓度值对比结果如下图10所示。
图10 H2O训练集实际浓度和预测浓度对比
由图10可看出利用训练集样本建立的模型对训练集本身做预测时效果较好,预测值能够很好的拟合真实值。对数据误差进行计算,结果可得训练集平均相对误差为0.138,相关系数为0.9482。分析可知GA-RBF模型相较于单独使用RBF而言,具有更好的回归预测能力,可以较为准确地预测样本中的H2O浓度信息。
将训练好的模型应用于测试集进行验证,测试集样本实际浓度值和预测浓度值对比如下图11所示。
图11 H2O测试集实际浓度和预测浓度对比
观察图11可知,GA-RBF模型的预测效果较好,将GA-RBF模型用于测试集的预测,其预测浓度值与实际浓度值能够较好的拟合,由此可推断GA-RBF模型可以用于混合气体中H2O浓度的定量分析。对数据误差进行计算,结果可得测试集平均相对误差为0.084,相关系数为0.9436。可知GA-RBF模型相比于单独使用RBF而言,具备较好的回归分析能力,可以较为准确地预测出H2O样本浓度信息。
GA-RBF算法在两气体组分训练集和测试集上预测的模型评价参数如表2所示:
由表2 GA-RBF模型的预测结果评价参数分析可知,其在混合气体组分定量识别问题中表现优异,模型优化效果较好。
4 结论
本文首先选取RBF神经网络算法用于混合气体组分浓度预测,将由HITRAN光谱数据库获取的100组混合气体样本数据集,随机分为训练集和测试集,其中训练集包含80组数据,测试集包含20组数据。经预处理输入至RBF神经网络模型,以混合气体组分CO2和H2O为研究对象,利用RBF网络模型分别对两种气体组分进行定量识别。由预测结果分析可知,RBF模型对两种气体组分的浓度预测精度均比较低,模型预测结果无法满足要求。因此为改进RBF网络对混合气体组分预测效果差的问题,考虑到模型参数对RBF网络回归预测精度的影响,本文在RBF网络的基础上提出了一种改进算法,即GA优化RBF网络用于混合气体组分浓度预测。通过GA优化RBF网络模型参数,获取最优参数组,再将优化后的模型用于混合气体组分定量识别。为排除实验随机性,选择与RBF网络预测算法相同的样本数据集上对比论证。实验结果表明,相较于单独使用RBF算法,GA-RBF优化模型在混合气体组分的定量识别问题中,表现更加优异。
参考文献:
[1]Ayslan S. P. Costa, Josefa M. S. Gon?alves, Hosana O. et al. Application of Near-Infrared for Online Monitoring of Heavy Fuel Oil at Thermoelectric Power Plants. Part I: Development of Chemometric Models[J]. Industrial & Engineering Chemistry Research,2019,58(34):550-558.
[2]El Khoury Youssef, Gebelin Marie, de Sèze Jér?me, et al. Rapid Discrimination of Neuromyelitis Optica Spectrum Disorder and Multiple Sclerosis Using Machine Learning on Infrared Spectra of Sera[J]. International Journal of Molecular Sciences, 2022,23(5):672-679
[3]张志峰. 基于直接吸收光谱的高浓度气体检测研究及甲烷气体检测样机开发[D]. 济南:山东大学,2022.
[4]翁静, 袁盼, 王铭赫, 等. 基于支持向量机的泄漏气体云团热成像检测方法[J]. 光学学报, 2022, 42(09):104-111.
[5]王玮. 基于气体传感器阵列的混合气体检测系统[D]. 西安:西北工业大学,2002.
[6]太惠玲, 谢光忠, 蒋亚东. 基于气体传感器阵列的混合气体定量分析[J].仪器仪表学报, 2006(07):666-670.
[7]Lei Zhang 0038, Fengchun Tian. Performance Study of Multilayer Perceptrons in a Low-Cost Electronic Nose.[J]. IEEE Trans. Instrumentation and Measurement, 2014,63(7):1670-1679.
[8]Ziteng Wen, Linbo Xie, Hongwei Feng, et al. Robust fusion algorithm based on RBF neural network with TS fuzzy model and its application to infrared flame detection problem[J]. Applied Soft Computing Journal, 2019,76:782-789.
[9]Duan Wenyang, Zhang Peixin, Huang Limin, et al. Ship hull surface reconstruction from scattered points cloud using an RBF neural network mapping technology[J]. Computers and Structures, 2023,281:209-215.
作者简介:吴广谱(1996— ),男,汉族,安徽宿州人,硕士(在读),学生,研究方向:红外光谱、混合气体成分识别与浓度检测。
