平和有乾坤,变化见功力
2024-06-23甄艳
甄艳

摘要:全面提升高三复习教学与复习备考的整体效益,是高三复习备考中最为重要的一个课题.本文中基于二轮复习,在“三新”背景下,依托“数列”专题,从重视教材、梳理知识、掌握性质、积累经验等层面来剖析相应的复习建议,为优化复习过程与提升复习效益作了一些尝试与经验积累.
关键词:数列;二轮复习;建议;知识;思想
在新课标、新教材、新高考的“三新”背景下,近年全国新高考数学试题的“数列”专题部分,随着新教学改革理念的逐步深入与延续,更加准确体现高考改革的要求,遵循数学课程标准的教学内容、学业要求和质量标准,以稳定性的考查方式、基础性的考查要求、全面性的考查内容以及创新性的考查情境等特点,全面突出基础性,彰显综合性,体现应用性,追求创新性,突出数学思想方法性等,合理聚焦数学学科核心素养,体现对数学关键能力的考查.
预测今后几年全国新高考数学试题的“数列”专题部分的考查,还是坚持“四性”,突出“四基”,夯实“四能”.由此,对于该专题的高考二轮复习,必须更有针对性与实用性,本文中从一些复习备考的尝试与建议入手,抛砖引玉.
1 重视数学教材,打好数学基础
作为高中课堂教学与学习的基石,教材是主要依据,更是课标标准的实际体现.因而在“数列”专题部分的二轮复习备考中,必须坚持围绕高中数学教材来展开,充分理解数列的基本概念与基本性质,以及一些相关的典型实例与性质应用等.通过通读教材,可以再次回顾相关的数学知识与应用场景.
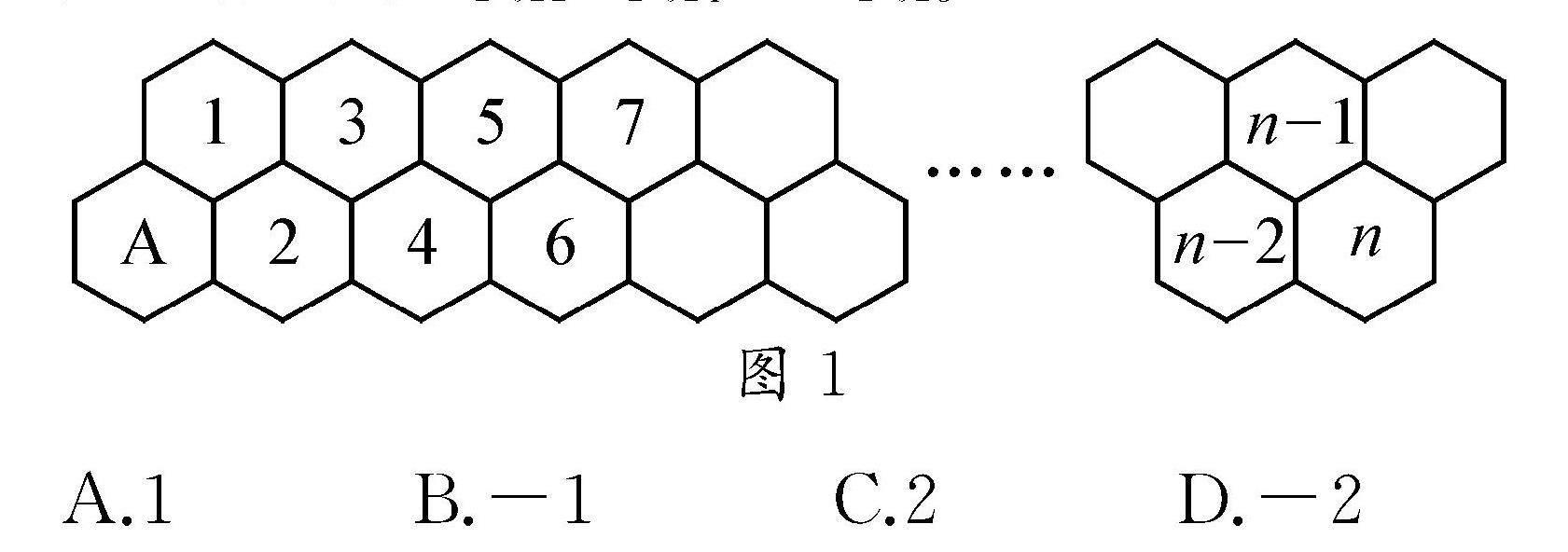
例1 〔2024届高三第一次学业质量评价(T8联考)数学试题〕一只蜜蜂从蜂房A出发向右爬,每次只能爬向右侧相邻的两个蜂房(如图1),例如,从蜂房A只能爬到1号或2号蜂房,从1号蜂房只能爬到2号或3号蜂房……以此类推,用an表示蜜蜂爬到n号蜂房的方法数,则a2 022a2 024-a22 023=( ).
A.1
B.-1
C.2
D.-2
通过问题场景,借助蜜蜂爬到前若干号蜂房的方法数,合理归纳,构建与之相吻合的斐波那契数列以及对应的数列递推关系式,借助所求数列项的代数关系式的特征,通过一般性思维与整体思维加以切入,利用等比数列的构建与应用来分析与处理,达到解决创新应用问题的目的.追根溯源,该问题场景源自教材中的“阅读与思考”栏目:
〔人民教育出版社2019年国家教材委员会专家委员会审核通过的《数学》(选择性必修第二册)第四章“数列”第10页阅读与思考——斐波那契数列〕
如果用Fn表示第n个月的兔子的总对数,其中F1=1,F2=1,F3=2,可以看出Fn=Fn-1+Fn-2(n∈N*,n>2).这是一个由递推公式给出的数列,称为斐波那契数列.
依托教材“阅读与思考”栏目的阅读材料,斐波那契数列一直是数列模块知识中最为常用的一种基本模型,也是全面考查数列模块“四基”与关键能力等最为重要的一个创新应用场景,备受各方关注.
在“数列”专题部分的二轮复习备考中,回归教材,借助教材中的一些典型例(习)题、探究性栏目等的回顾与探究,经常会有意想不到的收获.
2 梳理基础知识,归纳基本方法
在“数列”专题部分的二轮复习备考中,基础知识是绕不开的一个话题.特别是数列的基本概念,两个特殊数列的定义、通项与求和公式以及相关的基本性质等,都是数列研究的重要内容,有效构建起一个完整的数列知识体系.
因而,在数列专题的高考二轮复习备考时,要借助对应的数列知识体系,合理渗透相应的数学基本方法,如数列求解中的基本量法,数列通项的整体代换,数列的函数思维,组合与分解的方法,以及数列与不等式的放缩方法等,系统全面地掌握数列的知识以及解决问题的方法.
例2 〔2024届浙江省浙南名校联盟高三(上)第一次联考数学试卷〕已知数列{an}的首项为a1,且满足12Sn=4an+1+5n-13,其中Sn为其前n项和,若恒有Sn≤S4(n∈N*),则a1的取值范围为.
分析:根据数列的递推关系式来确定数列的通项公式,往往是解决与数列递推关系式相关问题中最为重要的一个基本步骤.解题的关键是利用前n项和Sn与通项an的关系进行变形与转化,通过关系式的结构特征,借助累加法、累乘法等加以合理变形与应用,是确定数列通项公式中比较常见的技巧方法.
解析:由12Sn=4an+1+5n-13,可得
12Sn+1=4an+2+5n+1-13.
以上两式对应相减,可得12an+1=4an+2-4an+1+4×5n,即an+2=4an+1-5n,n≥1.
整理,可得an+2+5n+1=4(an+1+5n),即
an+2+5n+1an+1+5n=4,n≥1.
所以a3+52a2+51=a4+53a3+52=……=an+5n-1an-1+5n-2=4,n≥3.
将以上(n-2)个式子累乘,可得an+5n-1a2+51=4n-2,即an+5n-1=4n-2×(a2+5),亦即
an=4n-2×(a2+5)-5n-1,n≥3.
而将n=1代入12Sn=4an+1+5n-13,可得12a1=4a2+5-13,整理有a2=3a1+2,所以an=4n-2×(3a1+7)-5n-1,n≥2.
而对于函数f(x)=4x-2×(3a1+7)-5x-1>0,可得54x-1<3a1+74.由指数函数的单调性,可知存在x
所以42×(3a1+7)-53≥0,43×(3a1+7)-54≤0,解得1348≤a1≤5964.
故a1的取值范围为1348,5964.
合理梳理数列中的基础知识,如涉及数列中前n项和Sn与通项an的递推关系式问题,可以利用an=S1,n=1,Sn-Sn-1,n≥2,结合an=Sn-Sn-1=f(an)-f(an-1)消去Sn,或利用Sn=f(Sn-Sn-1),消去an求解.而由知识上升为方法,如具体的解题步骤就是升降下标作差,运用通分、合并同类项、因式分解等,借助配凑法、累加(累乘)法、待定系数法等方法,将复杂、不熟悉的数列类型转化为特殊的等差数列或等比数列类型,在求解过程中往往要对数列的第一项、第二项等加以合理检验,避免出现差别与错误.
3 掌握基本性质,加强相互联系
在“数列”专题部分的二轮复习备考中,涉及数列的基本性质及其应用,要加以重点理解与把握,这也是高考命题中最为突出的基本点之一.特别是涉及选择题与填空题中数列的问题设置,经常离不开数列的基本性质与联系,因此熟练理解并掌握数列的基本性质也是高考解决好数列问题的关键之一.
因而,在数列专题的高考二轮复习备考时,特别要加强不同元素之间的联系,构建一个完整有机的整体,这样才方便形成联系,达到交汇与融合的目的.
例3 (2024届广东省佛山市南海区高三摸底考试数学试卷)已知数列{an}对任意k∈N*满足ak+1+ak=4k+3,则a1+a2 020=( ).
A.4 040
B.4 043
C.4 046
D.4 049
分析:根据数列的递推关系式加以合理数学运算(往往是相加或相减处理),分奇偶项分析,利用等差数列的确定与通项公式的转化来分析与求解.分奇偶项分别确定数列中相关项的基本性质,进而通过数列的奇偶项特征以及对应的特殊数列类型加以分析与解决问题.
解析:由ak+1+ak=4k+3,可得
ak+2+ak+1=4(k+1)+3=4k+7.
以上两式相减,可得ak+2-ak=4,所以数列{a2k},{a2k-1}均是以4为公差的等差数列,则有a2k=a2+4(k-1).
而a2+a1=4×1+3=7,则有a2k=a2+4(k-1)=7-a1+4(k-1)=4k+3-a1,所以a1+a2 020=4×1 010+3=4 043.
数列的基本性质的归纳与应用,往往是解决问题的关键所在.如解决以上涉及数列中的奇偶项综合问题,往往是抓住题设条件中数列的递推关系式的结构特征,通过多写几项的形式,从中合理观察,巧妙归纳,进而挖掘相应的性质与规律,为选择合适的技巧与方法提供思维方向.
在高考二轮复习备考中,整个复习备考过程也是一个知识积累与经验积累的过程.在这个积累过程中,不断强化与交汇,形成更高层次的解题习惯与方法,进而从中合理提炼出基本的数学思想方法.
基于此,在数列专题的高考二轮复习备考时,重视教材,梳理知识,掌握性质,积累经验等成为一个很好尝试,有效打好基础,优化归纳方法,巧妙加强联系,系统提炼思想,促进复习备考的提优增速.
今后几年高考数学“数列”专题试题着力创新情境的设置,优化难度的调控,更加突出新课程改革的要求与新高考的“指挥棒”,契合考试的人才选拔与高中的育人价值功能,充分体现“平和之中有乾坤,变化之处见功力”.
