基于mRMR-IPSO的短期负荷预测双阶段特征选择
2024-06-19焦龄霄周凯张子熙韩飞时伟君洪叶罗朝丰
焦龄霄 周凯 张子熙 韩飞 时伟君 洪叶 罗朝丰

doi: 10.11835/j.issn.1000-582X.2023.218
收稿日期:2023-03-20
网络出版日期:2023-12-07
基金项目:国网湖北电力公司科技项目(521520220006)。
Foundation:Supported by State Grid Hubei Electric Power Company Technology Project(521520220006).
作者简介:焦龄霄(1999—),女,主要从事电力负荷预测研究,(E-mail)13012183731@163.com。
摘要:电力负荷具有时空多变的特性,受众多因素的影响,在短期负荷预测中较多的输入特征会造成维度灾难,导致模型预测性能不佳,因此选择合理的输入特征集至关重要。文章提出一种新的短期负荷预测特征选择方法——mRMR-IPSO双阶段法。利用最大相关最小冗余(max-relevance and min-redundancy,mRMR)判据对原始特征进行排序,考虑输入特征与输出特征之间相关性和输入特征间冗余性,筛选掉一些排序靠后的特征,初选出对预测效果影响显著的特征子集;采用基于改进的粒子群优化算法(improved particle swarm optimization,IPSO)的搜索策略,以LightGBM模型的预测精度为适应度函数,对初选特征子集进行精选,得到最优特征子集。算例结果表明,所提方法能在对原始特征集大幅降维的情况下提升预测精度。
关键词:特征选择;负荷预测;最大相关最小冗余;改进的粒子群优化算法;LightGBM
中图分类号:TM715 文献标志码:A 文章编号:1000-582X(2024)05-098-12
Dual-stage feature selection for short-term load forecasting based on mRMR-IPSO
JIAO Lingxiao1, ZHOU Kai1, ZHANG Zixi1, HAN Fei1, SHI Weijun1, HONG Ye1, LUO Chaofeng2
(1. State Grid Hubei Extra High Voltage Company, Wuhan 430000, P. R. China; 2. State Grid Zhejiang Electric Power Co., Ltd. Huzhou Power Supply Company, Huzhou 313000, Zhejiang, P. R. China)
Abstract: Power load exhibits characteristics of temporal and spatial variation and is affected by various factors. In short-term load forecasting, an excessive number of input features can cause dimensionality disasters and lead to poor model prediction performance. Therefore, selecting a reasonable input feature set is crucial. This article proposes a novel feature selection method for short-term load forecasting–the mRMR-IPSO two-stage method. The max-relevance and min-redundancy (mRMR) criterion is employed to rank the original features, considering both the correlation between input and output features and the redundancy among input features. This process filters out less impactful features ranked lower and initially selects these significantly influencing the prediction. Then, an improved particle swarm optimization (IPSO) algorithm-based search strategy is adopted. The prediction accuracy of the LightGBM model is used as the fitness function during the search, facilitating the selection of primary feature subsets and obtaining optimal feature subsets. Calculation examples show that the proposed method improves prediction accuracy while substantially reducing the original feature set.
Keywords: feature selection; load forecasting; max-relevance and min-redundancy; improved particle swarm optimization algorithm; LightGBM
电力负荷受气象条件、经济因素和日类型等多种因素的影响,具有时空多变的特性,新能源的接入和电力市场的发展增加了负荷不确定性[1]。因此,需要设置多种类型的输入特征集来充分挖掘多源数据信息以应对电力负荷的波动性和随机性。但大量的输入特征将加重模型的收敛负担,导致模型预测性能的下降,进行合理的特征选择十分必要。
目前,短期负荷预测特征选择方法主要可以分为过滤(filter)法、包装(wrapper)法和嵌入(embedded)法。过滤法[2-8]以数据本身的统计特性来衡量特征重要性并确定选择的特征,时间复杂度低。丁坚勇等[2]基于Fisher信息进行特征选择;张振中等[3]根据最大互信息系数选出特征子集;徐先峰等[4]提出一种基于MIC(maximal information coefficient)的特征筛选策略;谷云东等[5]根据互信息和特征归因值选出最终特征子集;刘倩倩等[6]基于Person相关系数实现特征优选,但是PCC(pearson correlation coefficient)多用于线性关系的度量,难以度量负荷这类非线性变量;杨秀等[7]基于Copula函数对相关性进行定量计算;Abedinia等[8]提出考虑变量间相关、冗余和协同关系的特征选择方法。过滤法虽然时间复杂度低,但需要预先设定选择特征的阈值,因此其特征选择的主观性可能会对模型性能产生影响。包装法[9-10]从原始特征集中选择出使最终任务模型性能最佳的特征子集,如严雪颖等[9]提出基于遗传算法的搜索策略。包装法直接以模型性能为评价指标,所选特征集预测性能良好,但由于原始特征集的数量通常较多,其时间复杂度要远高于过滤法。嵌入法[11-12]包括基于树模型的特征选择和基于模型中惩罚项的特征选择,如孙超等[11]调用XGBoost模型训练中的权重和增益信息用于特征选择,朱凌建等[12]利用L1正则化将不重要的特征筛除。过滤法、包装法和嵌入法都各有优缺点,为充分利用其优势,一些学者提出了混合特征选择方法。Hu等[13]结合点互信息与萤火虫算法确定最优特征子集,郑睿程等[14]提出了一种将正交化最大信息系数、特征协同与随机森林递归消除相结合的混合特征选择方法。
为解决短期负荷预测原始特征集繁多冗余的问题,实现短期负荷预测特征降维与预测精度的提升。笔者根据负荷特性建立考虑多种因素的原始特征集,提出了一种基于最大相关最小冗余(max-relevance and min-redundancy,mRMR)与改进粒子群算法(improved particle swarm optimization,IPSO)结合的双阶段特征选择方法。在第一阶段,考虑相关性和冗余性采用mRMR对特征进行筛选,降低后续搜索时间复杂度;在第二阶段,以IPSO为最优特征子集搜索策略,精选最优特征子集,实现预测精度提升。以实际负荷数据集作为算例,验证了所提方法的可行性和优越性。
1 基于mRMR的特征选择
1.1 mRMR
互信息(mutal information, MI)作为一种有效的信息度量方法,不仅能够衡量变量间的线性关系,而且能很好地评估非线性关系[15]。
将2个随机变量x和y之间的互信息定义为
, (1)
式中:p(x)和p(y)分别为随机变量x和y的概率密度;p(x,y)为随机变量x和y的联合概率密度。
最大相关性和最小冗余性的定义分别为
; (2)
。 (3)
式中:S为特征集;|S|为特征集中的特征数目;y为目标变量;I(xi;y)为特征i和目标变量y之间的互信息;D为特征集中特征与目标变量y之间互信息的均值;I(xi;xj)为特征i和特征j之间的互信息;R为特征集中各特征之间的互信息。
对式(2)和式(3)组合,得到最大相关最小冗余准则[16]:
。 (4)
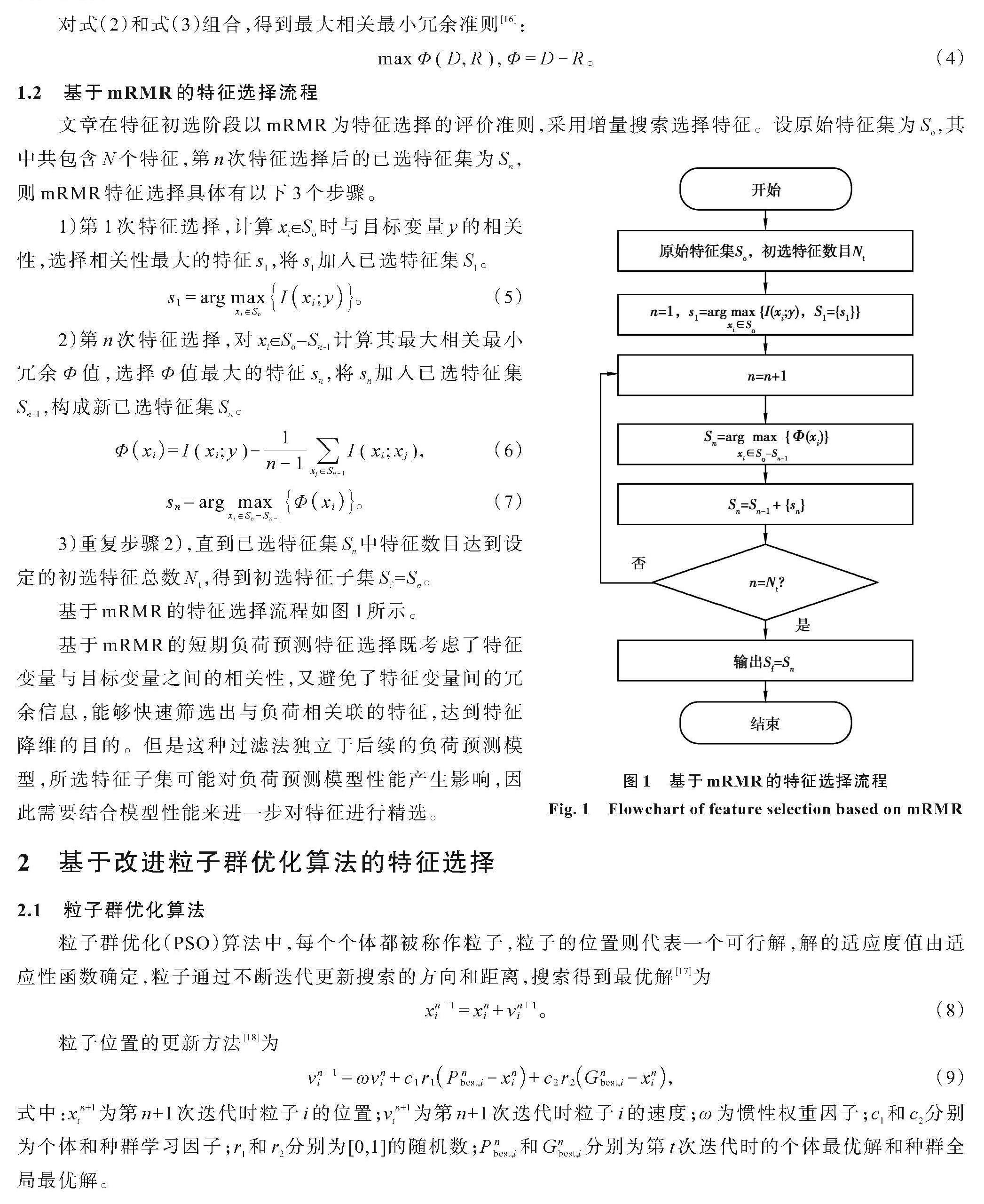
1.2 基于mRMR的特征选择流程
文章在特征初选阶段以mRMR为特征选择的评价准则,采用增量搜索选择特征。设原始特征集为So,其中共包含N个特征,第n次特征选择后的已选特征集为Sn,则mRMR特征选择具体有以下3个步骤。
1)第1次特征选择,计算xi∈So时与目标变量y的相关性,选择相关性最大的特征s1,将s1加入已选特征集S1。
。 (5)
2)第n次特征选择,对xi∈So-Sn-1计算其最大相关最小冗余Φ值,选择Φ值最大的特征sn,将sn加入已选特征集Sn-1,构成新已选特征集Sn。
, (6)
。 (7)
3)重复步骤2),直到已选特征集Sn中特征数目达到设定的初选特征总数,得到初选特征子集Sf=Sn。
基于mRMR的特征选择流程如图1所示。
基于mRMR的短期负荷预测特征选择既考虑了特征变量与目标变量之间的相关性,又避免了特征变量间的冗余信息,能够快速筛选出与负荷相关联的特征,达到特征降维的目的。但是这种过滤法独立于后续的负荷预测模型,所选特征子集可能对负荷预测模型性能产生影响,因此需要结合模型性能来进一步对特征进行精选。
2 基于改进粒子群优化算法的特征选择
2.1 粒子群优化算法
粒子群优化(PSO)算法中,每个个体都被称作粒子,粒子的位置则代表一个可行解,解的适应度值由适应性函数确定,粒子通过不断迭代更新搜索的方向和距离,搜索得到最优解[17]为
。 (8)
粒子位置的更新方法[18]为
, (9)
式中:xin+1为第n+1次迭代时粒子i的位置;vin+1为第n+1次迭代时粒子i的速度;ω为惯性权重因子;c1和c2分别为个体和种群学习因子;r1和r2分别为[0,1]的随机数;和分别为第t次迭代时的个体最优解和种群全局最优解。
2.2 改进粒子群算法
标准PSO算法粒子群进化后期存在早熟、易陷入局部最优的问题。为了增强PSO算法的全局搜索能力,提高特征选择的性能,引入莱维飞行(Lévy flight)、非线性变化惯性权重与时变学习因子来改进PSO算法。
2.2.1 莱维飞行策略
莱维飞行是一种随机搜索方法,它服从莱维分布和重尾分布,能实现短距搜索和偶尔长距的搜索相间的行走方式,具有良好的全局搜索能力[18]。
笔者结合莱维飞行提出一种Gbest调整策略,使粒子能够通过随机游走进行新的搜索,提高粒子群开发能力。Gbest调整策略为
, (10)
, (11)
式中:⊕为点对点乘法;α为步长控制量;LLevy(λ)为随机搜索路径。
2.2.2 非线性变化惯性权重
ω会影响粒子寻优能力,采用非线性递减的方式改进惯性权重。非线性变化惯性权重更新公式为
, (12)
式中:ωmax和ωmin分别为ω的最大值和最小值;Tmax为最大迭代次数。
2.2.3 时变学习因子
学习因子c1和c2对粒子寻优能力也有重要影响,采用时变学习因子代替原有学习因子常量。时变学习因子为
, (13)
, (14)
式中:c1max和c1min分别为c1的最大值和最小值;c2max和c2min分别为c2的最大值和最小值。
IPSO算法的伪代码如表1所示。
初始化粒子的速度vi和位置xi
计算粒子适应度pi
个体最优解pbest,i=pi
end for
gbest = min{pbest,i}
while t < max_iter
for i = 1 to N
根据式(12)~式(14)更新ω和c1、c2 10
11
12
13
14
15
16
17
18 根据式(8)~式(11)更新粒子的速度vi和位置xi
计算粒子适应度fit(xi)
if fit(xi) < fit(pbest,i)
pbest,i = xi
if fit(pbest,i) < fit(gbest)
gbest = pbest,i
end for
end while
输出 gbest
2.3 基于IPSO的特征选择流程
轻梯度提升机(light gradient boosting machine,LightGBM)不仅具有训练效果好、不易过拟合等优点,且较其他模型具有更快的训练速度和更低的内存开销[19],因此在IPSO特征选择阶段选用LightGBM模型为预测模型。在特征精选阶段以IPSO算法为最优特征搜索策略,以LightGBM短期负荷预测模型5折交叉验证的预测精度为指标进行特征精选。基于IPSO的特征选择具体有以下4个步骤。
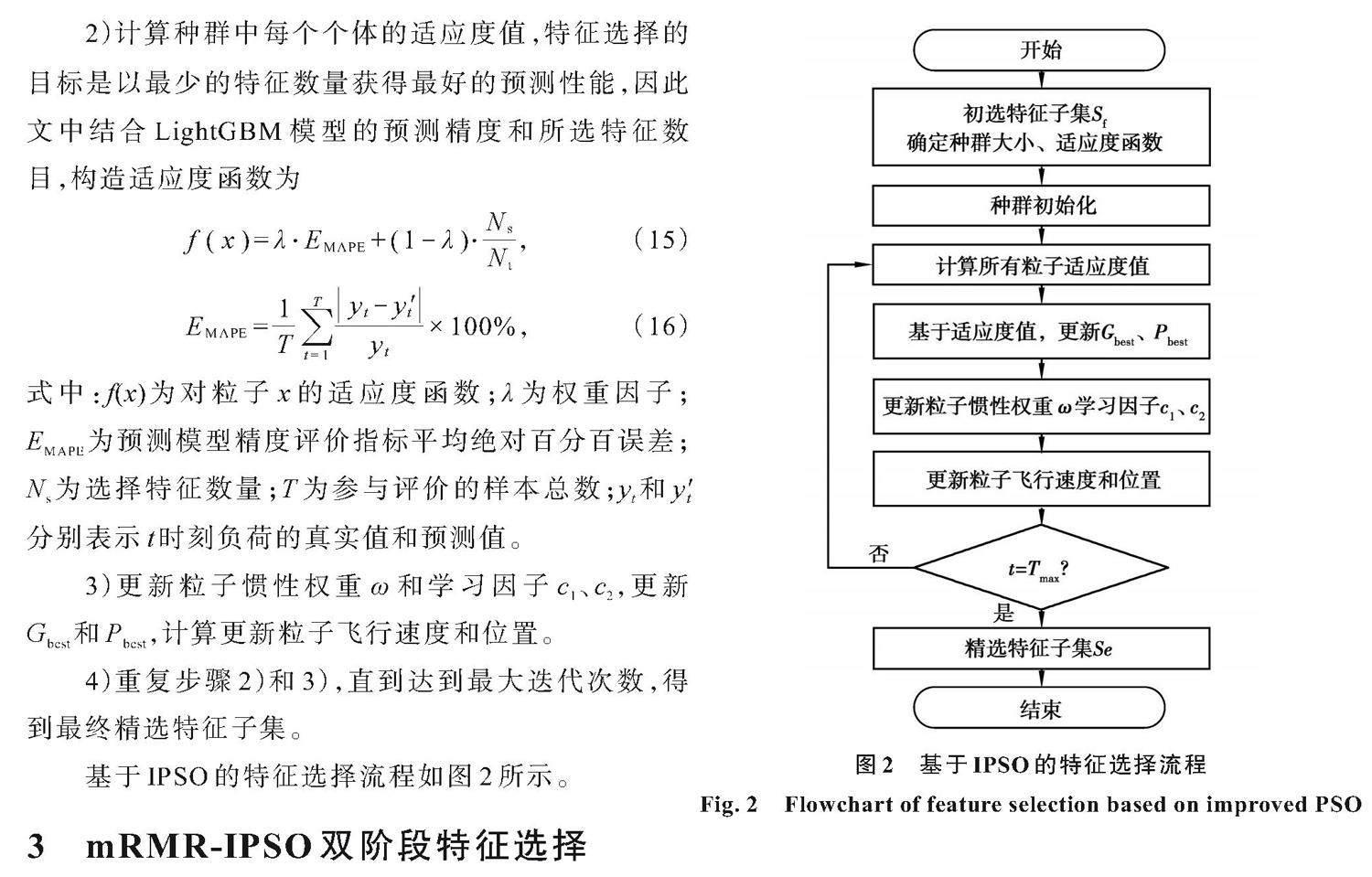
1)对初选特征子集Sf进行二进制编码,1表示该特征被选中,0则表示该特征未被选择,随机产生初始化种群。
2)计算种群中每个个体的适应度值,特征选择的目标是以最少的特征数量获得最好的预测性能,因此文中结合LightGBM模型的预测精度和所选特征数目,构造适应度函数为
, (15)
, (16)
式中:f(x)为对粒子x的适应度函数;λ为权重因子;EMAPE为预测模型精度评价指标平均绝对百分百误差;Ns为选择特征数量;T为参与评价的样本总数;yt和分别表示t时刻负荷的真实值和预测值。
3)更新粒子惯性权重ω和学习因子c1、c2,更新Gbest和Pbest,计算更新粒子飞行速度和位置。
4)重复步骤2)和3),直到达到最大迭代次数,得到最终精选特征子集。
基于IPSO的特征选择流程如图2所示。
3 mRMR-IPSO双阶段特征选择
由于负荷受多方面因素影响,构建的负荷数据集十分庞大,涉及特征数量众多,且短期负荷预测对预测模型精度要求较高,因此需要找到一种既能快速选择特征,又能满足精度要求的特征选择方法。基于mRMR的特征选择方法虽然能够实现关联特征的快速筛选,但所选特征子集的精度难以保证;基于IPSO的特征选择方法能够有效筛选出预测精度较高的特征子集,但对于短期负荷预测这种高维度的原始特征集,直接应用该方法耗时巨大,难以满足实际工程的需求。
结合过滤法和包装法的优势,提出mRMR-IPSO双阶段特征选择方法,流程如图3所示。
mRMR-IPSO双阶段特征选择方法具体步骤如下:
1)根据短期负荷预测数据集特点,选取合适的原始特征集So。
2)进行数据预处理,采用min-max标准化对数据进行预处理以消除量纲不同的影响。
3)采用基于mRMR的短期负荷预测特征选择,快速筛选与负荷相关联的特征,得到初选特征子集Sf。
4)采用基于IPSO的短期负荷预测特征选择,对初选特征子集进行精选,得到精选特征子集Se。
4 短期负荷预测原始特征集的构建
以澳大利亚某地区多维负荷数据为样本,数据集包含了该地区2006—2010年5年内的负荷及温度信息,每30 min采样一次。综合文献[4, 9, 13],从日历规则特征、天气影响特征和历史负荷特征3个方面构建日前短期负荷预测原始特征集。
4.1 日历规则特征
该地区2006—2010年的负荷曲线如图4(a)所示,2006年4月连续4周的负荷曲线如图4(b)所示。可以看出,负荷在各年和各周基本都呈现出相似的周期变化规律。
该地区2006年4月一周内7天的负荷曲线如图4(c)所示。从图中可以看出,日负荷的变化趋势大致相同,但周一到周五的负荷明显高于周六和周日的负荷,这是由于人们的工作和休息习惯导致的。
结合上述分析,选取了待预测的时刻、对应的月份、当月第几日、当周第几日以及是否为工作日这5个特征作为日历规则特征。
4.2 天气影响特征
该地区2010年负荷与温度的关系如图5所示。从图中可以看出,当温度从0 ℃上升到15 ℃时,负荷逐渐减小;当温度从15 ℃上升到40 ℃时,负荷逐渐上升。值得注意的是,温度还具有累积效应,连续多日的高温或低温与某一日单独的高温或低温对负荷的影响有很大差异,因此在构建温度特征时,需对其加以考虑。
结合上述分析,研究选取了时间段[t-24, t]的日内平均温度Tavg(t)、日内最高温度Tmax(t)、日内最低温度Tmin(t)和滞后温度Th为天气影响特征。滞后温度Th=T(t-h)代表h小时前的温度。
同时为反应温度变量的变化趋势,引入温度的一阶导数和二阶导数作为特征。其计算公式为
, (17)
。 (18)
4.3 历史负荷特征
历史负荷变量与温度变量均为连续性变量,选择的历史负荷特征与温度特征类似,不再多加赘述。
最终构造的短期负荷预测原始特征集如表2所示,共包含了87个特征。
表2 短期负荷预测原始特征集
Table 2 Original feature set for short-term load forecasting
特征类型 特征名 数量
日历规则特征 Chour、Cmonth、Cday、Cweek、Cwow 5
天气影响特征 Th,h∈{0,0.5,…,23.5};T24d,d∈{1,2,…,7};Tavg(t);Tmax(t);Tmin(t);; 60
历史负荷特征 L24d, d∈{1,2,…,7};Lavg(t-24d), d∈{1,2,…,7};Lmax(t-24d) ,d∈{1,2,…,7};Lmin(t-24d), d∈{1,2,…,7};L-24d, d∈{2,3,…,7};, d∈{2,3,…,7} 22
日历规则特征中,Chour用0~23.5表示时刻,Cmonth用1~12表示月份,Cday用1~31表示当月第几日,Cweek用1~7表示当周第几天,Cwow用0或1表示工作日或非工作日;天气影响特征中,Th表示预测时刻前h小时温度,T24d表示预测日前d天该时刻温度,Tavg(t)、Tmax(t)和Tmin(t)分别表示时间段[t-24,t]的日内平均温度、日内最高温度和日内最低温度,和分别表示预测时刻温度的一阶导数和二阶导数;历史负荷特征中,L24d表示预测日前d天该时刻负荷,Lavg(t-24d)、Lmax(t-24d)和Lmin(t-24d)分别表示时间段[t-24d-24, t-24d]的日内平均负荷、日内最高负荷和日内最低负荷,L-24d和分别表示预测日前d天该时刻负荷的一阶导数和二阶导数。
5 算例分析
5.1 实验数据和平台
以澳大利亚某地区2006—2010年5年的负荷数据和气象数据作为实验数据集,以前4年的数据为训练集,以最后1年的数据为测试集,进行特征选择和日前短期负荷预测。
5.2 实验评价指标
为验证所提特征选择方法的有效性,采用5折交叉验证的方式,验证测试集的预测精度,采用平均绝对百分误差EMAPE和均方根误差ERMSE作为预测模型的评价指标,EMAPE如式(16)所示,ERMSE如式(19)所示。
。 (19)
5.3 参数设置
在mRMR特征选择阶段设定初选特征子集中特征数目Nt为40;在IPSO特征选择阶段,参考文献[20]设置IPSO算法参数如下:粒子种群规模为10,最大迭代次数Tmax为50次,惯性权重最大值ωmax为0.9,最小值ωmin为0.4,学习因子c1的最大值c1max和最小值c1min分别为2.5和0.5,c2的最大值c2max和最小值c2min分别为2.5和0.5,适应度函数中的权重因子λ为0.75;采用网格搜索法设置LightGBM超参数如下:树深度为7,学习率为0.1,叶子数为30,特征抽样比为0.8,正则化参数分别为0.09和0。
5.4 IPSO算法性能分析
为验证所提IPSO算法在短期负荷预测特征选择上的寻优性能,采用标准PSO算法和遗传算法(genetic algorithm,GA)进行对比。3种算法的迭代曲线如图6所示。
分析图6可得,改进的PSO算法较标准PSO算法和GA算法表现最优。与GA算法相比,IPSO算法收敛速度稍慢,但其寻优结果明显优于GA算法;与标准PSO算法相比,标准PSO算法出现了早熟收敛的情况,而IPSO算法通过引入莱维飞行、非线性变化惯性权重与时变学习因子增强了算法的全局寻优能力,使粒子群能够跳出局部搜索,有更好的全局收敛性。
每次迭代后,粒子群中最优个体的预测误差EMAPE和所选特征数量NS的变化情况如图7所示。
从图7中可以看出,在迭代过程中预测误差和特征数量都在不断更新变化,在迭代开始时,所选特征数量较多且模型预测精度不佳,而随着粒子种群的迭代,所选特征的数量和预测误差都在不断缩小,最终得到了特征数量最少且预测误差最低的最优特征子集。
5.5 不同特征选择方法对比
5.5.1 与过滤式特征选择方法对比
为验证所提特征选择方法的优越性,采用PCC、MI、ReliefF和mRMR这4种过滤式特征选择方法进行对比测试,并采用LightGBM预测模型进行日前短期负荷预测。采用过滤式特征选择方法时,根据所选方法对原始特征集中特征进行降序排序,得到初选特征子集,然后从初选特征子集中按顺序选出前n(个特征构成相继的特征子集,基于LightGBM算法根据交叉验证精度得到对应的最优特征子集。不同特征选择方法的特征选择结果和预测效果如表3所示。
表3 过滤法的特征选择结果及预测效果
Table 3 Feature selection results and forecast results of filter
特征选择方法 特征数量 特征子集 EMAPE/% ERMSE/MW
PCC 40 Chour;Cwow;Th, h∈{8,8.5,…,17.5};L24d, d∈{1,2,…,7};Lavg(t-24d), d∈{2,7};Lmax(t-24d),d∈{1,2,7};Lmin(t-24d), d∈{1,2,7};, d∈{2,3,7} 2.84 373.388
MI 39 Chour;Th, h∈{0,0.5,1,1.5,11,…,16};Tavg(t);L24d, d∈{1,2,…,7};Lavg(t-24d), d∈{7};Lmax(t-24d), d∈{7};Lmin(t-24d), d∈{7} 2.77 361.758
ReliefF 24 Chour;Cweek;Cwow;Th, h∈{0,0.5,1,1.5,9,9.5,10,10.5};L24d, d∈{1,2,…,7};, d∈{2,3,7};, d∈{7} 2.20 297.782
mRMR 29 Chour;Cmonth;Cday;Cweek;Cwow;Th, h∈{0,10.5,22.5};T24d, d∈{2};;;L24d, d∈{1,2,…,7};Lavg(t-24d), d∈{2,7};Lmax(t-24d), d∈{2,3,7};Lmin(t-24d), d∈{7};, d∈{3,7};, d∈{2,3,7} 2.15 285.101
mRMR-IPSO 17 Chour;Cmonth;Cday;Cweek;Cwow;Th, h∈{0,22.5};T24d, d∈{3,6};;;L24d, d∈{1,3,4};Lmax(t-24d), d∈{7};,d∈{2} 1.99 265.956
从表3中可知:
1)所用对比方法中,只有mRMR与mRMR-IPSO完整地选择出了所有的日历规则特征,其他方法均漏选了某些日历规则特征。而预测结果也表明日历规则特征的重要性。
2)天气影响特征在各方法所选特征子集中均占有较大比重,PCC、MI和ReliefF所选天气影响特征存在严重的冗余现象,mRMR减少了冗余特征,mRMR-IPSO仅选择出了少量的天气影响特征,但仍然达到了最优的预测精度。
3)所有过滤法均选择了前一周相应时刻的历史负荷变量。PCC选择的历史负荷特征冗余现象严重,这是因为PCC不适用于非线性关系的衡量。mRMR-IPSO所选历史负荷特征最少。
4)在过滤法中mRMR性能最优,这是因为mRMR既考虑了变量间相关性,又最大限度地减少了冗余变量,而mRMR-IPSO在mRMR的基础上对变量进行了精选,所选特征维数较mRMR减少了41.4%,特征子集数量最少,且预测精度最高。
所提mRMR-IPSO短期负荷预测特征选择方法所选的特征子集维数在所有方法中是最少的,只有17维,比原始特征集减少了80.4%,预测误差EMAPE为1.99%,ERMSE为265.956 MW,较PCC特征选择预测误差减少了29.9%,预测性能最优。mRMR-IPSO在测试集中一周内的预测结果及误差如图8所示,除在负荷高峰时段预测误差稍大外,其他时段预测误差基本都在1.5%以内,预测性能优良。
为进一步比较各特征选择方法在不同预测场景下的预测性能,基于不同特征选择方法在2010年各月份的预测结果如图9所示。
从图9可以看出,夏季(12月、1月、2月)的预测误差最大,冬季(6月、7月、8月)次之,春秋两季预测误差最小。这是由于夏季和冬季负荷受温度影响波动较大导致的。而mRMR-IPSO不论在哪一月份均都有最佳的表现,在5月预测误差最低仅为1.20%,且在最难预测的1月,预测误差也只有3.05%,预测精度较PCC提升了41.8%,这体现了mRMR-IPSO在负荷波动较大情况下的预测优势,体现了该方法的稳定性。
5.5.2 与混合式特征选择方法对比
为验证所提2阶段特征选择的阶段结合有效性,采用包装法中的基于LightGBM模型的递归特征消除法(recursive feature elimination, RFE)、前向序列选择法(sequential forward selection, SFS)和IPSO特征选择法结合上文所采用的过滤式特征选择方法组成2阶段混合特征选择方法,进行对比测试,其中RFE方法可以自动得出最优特征子集数目,SFS需要预先指定选择特征数目,设定为17,与mRMR-IPSO选择特征数目一致。基于上述特征选择方法,采用LightGBM模型预测得到预测结果如表4所示。
从表4中可知,包装法与过滤法结合的特征选择方法能有效提升预测性能,其中IPSO在包装法中表现最佳,与各过滤法结合时都较单一过滤法有更好的表现。在混合法中,过滤法的选择也对预测性能有重大影响,PCC和MI在单一过滤法中表现不佳,因此与包装法结合后虽然性能有一定提升,预测效果仍然不及其他混合法。mRMR-IPSO将过滤法和包装法中2种最优的方法结合在一起,在混合法中得出了最优的预测效果。需要指出的是,虽然mRMR-SFS也表现出了较高的预测精度,但是由于SFS是一种贪心算法,训练耗时巨大,且在对比试验中该方法所选特征数量是根据mRMR-IPSO所选特征数目提前设定的,而在实际应用中,最优特征子集的数量通常都是未知的,mRMR-IPSO和mRMR-SFS相比,不仅训练耗时短,且能够自动选择最佳特征子集数目,性能更优越。
5.6 其他预测模型预测结果
为验证所提特征选择方法的普适性,采用短期负荷预测常用的深度置信网络(deep belief network,DBN)和随机森林(random forest,RF)预测模型来进行对比测试,特征选择方法采用过滤法中效果最佳的mRMR特征选择方法和混合法中效果最佳的mRMR-SFS特征选择方法,采用不同预测模型的预测结果如表5所示。
从表5中可知,在不同模型下,mRMR-IPSO选出的特征子集预测精度都是最优的,这表明了该方法具有一定的稳定性,能够适用于不同的预测模型。
6 结 论
文章进行了短期负荷预测特征选择研究,提出了一种mRMR-IPSO短期负荷预测特征选择方法,通过mRMR对原始特征集进行初选,采用改进的PSO对初选特征子集进行精选,得到最优特征子集。基于数据集进行算例仿真,验证了所提方法的有效性,得到结论如下:
1)mRMR-IPSO特征选择方法既考虑了变量间相关性与冗余性,又考虑了特征选择对预测精度的影响,mRMR过滤法快速初选特征,IPSO法实现预测精度的提升,实现了特征选择时间复杂度与预测精度的平衡。
2)mRMR-IPSO特征选择方法能够在对原始特征集进行大幅降维的情况下,选出最优的特征子集,且预测精度优于其他过滤特征选择方法和混合特征选择方法,在各个场景下均具有很高的预测精度。
3)mRMR-IPSO特征选择方法对其他短期负荷预测模型同样适用,较其他特征选择方法,在不同预测模型上表现同样最优。
参考文献
[1] 林涵, 郝正航, 郭家鹏, 等. 基于TCA-CNN-LSTM的短期负荷预测研究[J].电测与仪表, 2023, 60(8):73-80.
Lin Han, Hao Z H, Guo J P, et al. Research on short-term load forecasting based on TCA-CNN-LSTM[J]. Electrical Measurement & Instrumentation, 2023, 60(8):73-80. (in Chinese)
[2] 丁坚勇, 朱炳翔, 田世明, 等. 改进F-score特征选择的MPSO-BP神经网络短期负荷预测[J]. 电测与仪表, 2018, 55(15): 36-41.
Ding J Y, Zhu B X, Tian S M, et al. Short-term load forecasting of MPSO-BP neural network based on improved F-score feature selection[J]. Electrical Measurement & Instrumentation, 2018, 55(15): 36-41. (in Chinese)
[3] 张振中, 郭傅傲, 刘大明, 等. 基于最大互信息系数和小波分解的多模型集成短期负荷预测[J]. 计算机应用与软件, 2021, 38(5): 82-87.
Zhang Z Z, Guo F A, Liu D M, et al. Multi-model integrated short-term load prediction based on maximum mutual information coefficient and wavelet decomposition[J]. Computer Applications and Software, 2021, 38(5): 82-87. (in Chinese)
[4] 徐先峰, 赵依, 刘状壮, 等. 用于短期电力负荷预测的日负荷特性分类及特征集重构策略[J]. 电网技术, 2022,46(4):1548-1556.
Xu X F, Zhao Y, Liu Z Z, et al. Daily load characteristic classification and feature set reconstruction strategy for short-term power load forecasting [J]. Power System Technology, 2022,46(4):1548-1556. (in Chinese)
[5] 谷云东, 刘浩. 基于最优特征组合改进极限梯度提升的负荷预测[J]. 计算机应用研究, 2021, 38(9): 2767-2772.
Gu Y D, Liu H. Load forecasting based on optimal feature combination improved XGBoost[J]. Application Research of Computers, 2021, 38(9): 2767-2772. (in Chinese)
[6] 刘倩倩, 刘钰山, 温烨婷, 等. 基于PCC-LSTM模型的短期负荷预测方法[J]. 北京航空航天大学学报, 2022, 48(12): 2529-2536.
Liu Q Q, Liu Y S, Wen Y T, et al. Short-term load forecasting method based on PCC-LSTM model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(12): 2529-2536. (in Chinese)
[7] 杨秀, 陈斌超, 朱兰, 等. 基于相关性分析和长短期记忆网络分位数回归的短期公共楼宇负荷概率密度预测[J]. 电网技术, 2019, 43(9): 3061-3071.
Yang X, Chen B C, Zhu L, et al. Short-term public building load probability density prediction based on correlation analysis and long-and short-term memory network quantile regression[J]. Power System Technology, 2019, 43(9): 3061-3071. (in Chinese)
[8] Abedinia O, Amjady N, Zareipour H. A new feature selection technique for load and price forecast of electrical power systems[J]. IEEE Transactions on Power Systems, 2017, 32(1): 62-74.
[9] 严雪颖, 秦川, 鞠平, 等. 负荷功率模型的最优特征选择研究[J]. 电力工程技术, 2021, 40(3): 84-91.
Yan X Y, Qin C, Ju P, et al. Optimal feature selection of load power models [J]. Electric Power Engineering Technology, 2021, 40(3): 84-91.(in Chinese)
[10] Jiang P, Liu F, Song Y L. A hybrid forecasting model based on date-framework strategy and improved feature selection technology for short-term load forecasting[J]. Energy, 2017, 119: 694-709.
[11] 孙超, 吕奇, 朱思曈, 等. 基于双层XGBoost算法考虑多特征影响的超短期电力负荷预测[J]. 高电压技术, 2021, 47(8): 2885-2898.
Sun C, Lü Q, Zhu S T, et al. Ultra-short-term power load forecasting based on two-layer XGBoost algorithm considering the influence of multiple features[J]. High Voltage Engineering, 2021, 47(8): 2885-2898. (in Chinese)
[12] 朱凌建, 荀子涵, 王裕鑫, 等. 基于CNN-Bi LSTM的短期电力负荷预测[J]. 电网技术, 2021, 45(11): 4532-4539.
Zhu L J, Xun Z H, Wang Y X, et al. Short-term power load forecasting based on CNN-BiLSTM[J]. Power System Technology, 2021, 45(11): 4532-4539. (in Chinese)
[13] Hu Z Y, Bao Y K, Xiong T, et al. Hybrid filter-wrapper feature selection for short-term load forecasting[J]. Engineering Applications of Artificial Intelligence, 2015, 40: 17-27.
[14] 郑睿程, 顾洁, 金之俭, 等. 数据驱动与预测误差驱动融合的短期负荷预测输入变量选择方法研究[J]. 中国电机工程学报, 2020, 40(2): 487-500.
Zheng R C, Gu J, Jin Z J, et al. Research on short-term load forecasting variable selection based on fusion of data driven method and forecast error driven method[J]. Proceedings of the CSEE, 2020, 40(2): 487-500. (in Chinese)
[15] 李扬, 顾雪平. 基于改进最大相关最小冗余判据的暂态稳定评估特征选择[J]. 中国电机工程学报, 2013, 33(34): 179-186, 27.
Li Y, Gu X P. Feature selection for transient stability assessment based on improved maximal relevance and minimal redundancy criterion[J]. Proceedings of the CSEE, 2013, 33(34): 179-186, 27. (in Chinese)
[16] Peng H C, Long F H, Ding C. Feature selection based on mutual information: criteria of max-dependency, max-relevance, and Min-redundancy[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(8): 1226-1238.
[17] Kennedy J, Eberhart R. Particle swarm optimization[C]//Proceedings of ICNN'95-International Conference on Neural Networks. IEEE, 2002: 1942-1948.
[18] Yadav S, Ekbal A, Saha S. Feature selection for entity extraction from multiple biomedical corpora: a PSO-based approach[J]. Soft Computing, 2018, 22(20): 6881-6904.
[19] Zhang Y Y, Zhu C F, Wang Q R. LightGBM-based model for metro passenger volume forecasting[J]. IET Intelligent Transport Systems, 2020, 14(13): 1815-1823.
[20] 王生亮, 刘根友. 一种非线性动态自适应惯性权重PSO算法[J]. 计算机仿真, 2021, 38(4): 249-253, 451.
Wang S L, Liu G Y. A nonlinear dynamic adaptive inertial weight particle swarm optimization[J]. Computer Simulation, 2021, 38(4): 249-253, 451. (in Chinese)
(编辑 詹燕平)
