康普顿散射的可视化研究

摘要：为了澄清对康普顿散射过程中存在的误解，增加对康普顿散射的直观理解，首先辨析了光电效应和康普顿散射实验的异同，随后对康普顿碰撞的理论进行了详细推导，并基于MATLAB对康普顿散射进行了模拟.研究表明：康普顿散射波长改变量的增长率和反冲电子获得的能量以及动量增长率均随散射角的增大而增加.但反冲电子的动量增长率比能量增长率随角度的变化表现得更为明显和剧烈.在散射角一定的情况下，反冲电子的动量和能量增长率均随入射光波长的减小而增加.最后讨论了康普顿散射的物理意义.

关键词：康普顿效应；散射；光量子；可视化

中图分类号：O413文献标志码：A

Visualization of Compton Scattering

ZHANG Lei， CAO Xinwei

（School of Mechanical and Material Engineering， Xi’an University， Xi’an 710065，China）

Abstract： In order to clarify the misunderstandings of Compton scattering process and increase the intuitive understanding of it， the differences and similarities between the photoelectric effect and the Compton scattering experiment is first analyzed， then the theory of Compton collision is derived in detail， and the Compton scattering is simulated based on MATLAB. The study results show that： with the increase of scattering angle， the growth rate of Compton scattering wavelength change and the growth rate of recoil electron’s energy and momentum both show an upward trend. However， compared with the growth rate of energy， the growth rate of recoil electron’s momentum is more significant and dramatic in the aspect of angle change. At a given scattering angle， the growth rate of recoil electron’s momentum and energy will also increase with the decrease of incident light wavelength. Finally， the physical significance of Compton scattering is discussed.

Key words： Compton effect; scattering; photon; visualization

普朗克被称为“量子力学之父”，是因为他在解决黑体辐射时提出的普朗克能量子假说，它标志着量子论的诞生.从经典物理学的眼光来看，吸收或发射的能量是不连续的，而是一份一份的，只能是某个最小能量的整数倍，即能量的量子化假设是如此不可思议.在量子物理教学过程中，理解光的粒子性和电子的波动性最具代表性的实验是光电效应和康普顿效应．这两种效应都是电磁波和物质的相互作用过程，但是光电效应中入射的电磁波为可见光波段（400～760 nm），康普顿效应入射的电磁波为X射线波段（0.1～1 nm）.在光电效应中光子能量全部被电子吸收；而康普顿效应中光子和电子发生碰撞，使光子失去一部分能量而偏离原来“飞行”方向.一定频率的电磁波入射，发生两种效应的概率不同，这由光子的能量和散射原子的质量而定，一般来说发生光电效应的几率随光子的能量增大而减小.康普顿效应实验有力地支持了光子学说理论的正确性，通过实验发现光子具有质量、动量和能量等粒子具有的物理特性；同时也证实了光子、电子等微观粒子基元间相互作用时，同样严格遵守能量守恒定律和动量守恒定律，即动量守恒定律和能量守恒定律在相对论的意义上仍然成立［1］.

笔者发现在许多教学案例和教学过程中，为了阐述清楚康普顿散射实验，大家常引用经典的弹性小球的碰撞模型来解释，得出的结论虽然也能与实验相符，但该模型只考虑到系统的初态和末态，没有涉及光子和电子相互作用的中间过程.按照弹性碰撞的理想模型分析，入射光子与电子碰撞后损失了一部分能量，损失的部分能量传递给电子，导致自己能量损失而使频率降低的一些错误结论［2］.这是与爱因斯坦的光子不可分的概念相违背.其次，学生在学习量子物理时对微观粒子波粒二象性认识不充分，不能理解光与物质的相互作用的过程，特别是与光电效应相比较时就容易产生很大的疑惑.另外，普通高校的近代物理实验室很难完成该实验，因此对康普顿效应实验的研究有一定的可行性［3］.为了直观认识康普顿散射的特点，采用MATLAB软件来数值模拟康普顿散射实验，将枯燥的理论知识形象化，有利于增强学生学习兴趣.

1康普顿效应实验

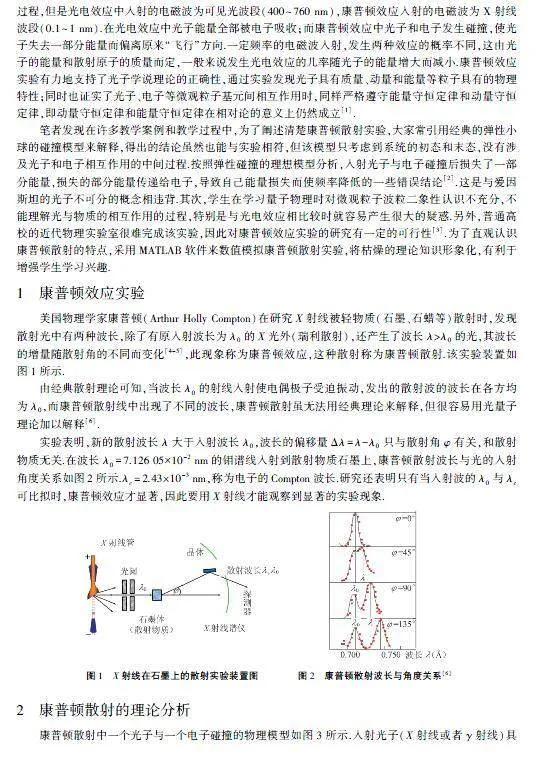
美国物理学家康普顿（Arthur Holly Compton）在研究X射线被轻物质（石墨、石蜡等）散射时，发现散射光中有两种波长，除了有原入射波长为λ0的X光外（瑞利散射），还产生了波长λgt;λ0的光，其波长的增量随散射角的不同而变化［4-5］，此现象称为康普顿效应，这种散射称为康普顿散射.该实验装置如图1所示.

由经典散射理论可知，当波长λ0的射线入射使电偶极子受迫振动，发出的散射波的波长在各方均为λ0，而康普顿散射线中出现了不同的波长，康普顿散射虽无法用经典理论来解释，但很容易用光量子理论加以解释［6］.

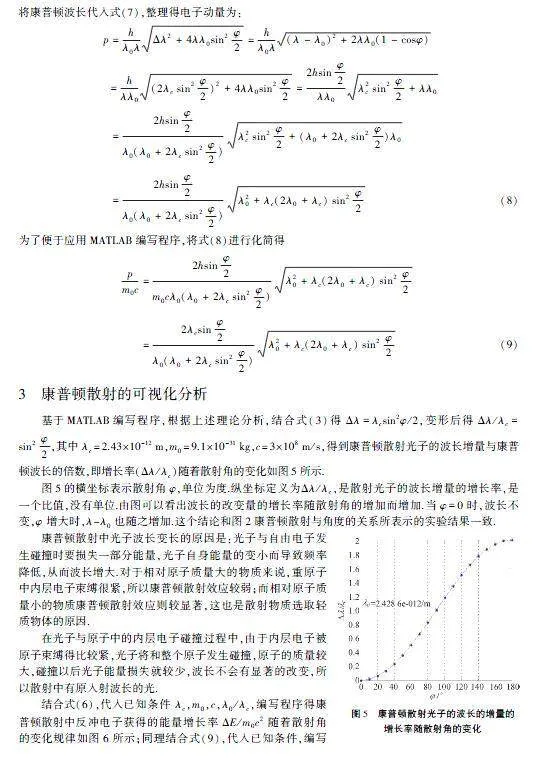
实验表明，新的散射波长λ大于入射波长λ0，波长的偏移量Δλ=λ－λ0只与散射角φ有关，和散射物质无关.在波长λ0=7.126 05×10－2 nm的钼谱线入射到散射物质石墨上，康普顿散射波长与光的入射角度关系如图2所示.λc=2.43×10－3 nm，称为电子的Compton波长.研究还表明只有当入射波的λ0与λc可比拟时，康普顿效应才显著，因此要用X射线才能观察到显著的实验现象.

2康普顿散射的理论分析

康普顿散射中一个光子与一个电子碰撞的物理模型如图3所示.入射光子（X射线或者γ射线）具有很大的能量，能量值范围在104～105 ev.固体表面的电子束缚较弱，可近视为自由电子.电子热运动的平均能量量级为10－2 ev，远小于光子的能量，因此可近似为静止的电子.与光子碰撞电子的反冲速度很大，必须采用相对论力学来处理.

康普顿散射过程中将原子中的电子看成是自由的和静止的，康普顿散射可以看作是X射线中的光子和自由电子间的弹性碰撞，康普顿散射中光子和电子碰撞的动量关系如图4所示. 考虑碰撞过程中的能量守恒和动量守恒，以及狭义相对论质量关系和相对论效应得到下面式子.

hυ0+m0c2=hυ+mc2hυ0ce→0=hυce→+mv→（1）

m=m01－v2c2（2）

上式中h为普朗克常数，h=6.63×10－34" J·S，频率为υ0的X射线可看成是由能量为ε=hυ0的光子组成的，碰撞后散射光子的频率为 υ；

电子碰撞前后的静质量和相对论质量分别为m0和 m

，由狭义相对论的质能关系可知，其相应的能量为m0c2和mc2；e→0和e→分别为碰撞前后光子运动方向上的单位矢量，v→为碰撞后电子的反冲速度.

将上面式子联立求解得散射波长的改变量：

Δλ=λ－λ0=cυ－cυ0=hm0c（1－cosφ）=2hm0csin2φ2（3）

其中定义康普顿波长

λc=hm0c=2.43×10－3 nm（4）

根据能量守恒定律，可得碰撞后电子获得的能量，即为碰撞过程中光子损失的能量.

ΔE=hυ0－hυ=hcλ0－hcλ=hcΔλλ0λ=2hcλcsin2φ2λ0（λ0+2λcsin2φ2）（5）

为了便于应用MATLAB编写程序，将式（5）再进行化简得

ΔEm0c2=2hcλcsin2φ2m0c2λ0（λ0+2λcsin2φ2）=2λ2csin2φ2λ0（λ0+2λcsin2φ2）（分子分母同时除以λ2c ）

=2sin2φ2λ0λc（λ0λc+2sin2φ2）（6）

由碰撞过程中的动量守恒，得出碰撞后电子的动量大小为：

p=（hλ0）2+（hλ）2-

2（hλ0）（hλ）cosφ=

hλ0λλ2+λ20-2λλ0cosφ

（7）

将康普顿波长代入式（7），整理得电子动量为：

p=hλ0λΔλ2+4λλ0sin2φ2=hλ0λ（λ－λ０）２＋２λλ０（1-cosφ）

=hλλ0（2λcsin2φ2）2+

4λλ0sin2φ2=2hsinφ2λλ0λ2csin2φ2+λλ0

=2hsinφ2λ0（λ0+2λcsin2φ2）λ2csin2φ2+（λ0+2λcsin2φ2）λ0

=2hsinφ2λ0（λ0+2λcsin2φ2）λ20+λc（2λ0+λc）sin2φ2（8）

为了便于应用MATLAB编写程序，将式（8）进行化简得

pm0c=2hsinφ2m0cλ0（λ0+2λcsin2φ2）λ20+λc（2λ0+λc）sin2φ2

=2λcsinφ2λ0（λ0+2λcsin2φ2）λ20+λc（2λ0+λc）sin2φ2（9）

3康普顿散射的可视化分析

基于MATLAB编写程序，根据上述理论分析，结合式（3）得Δλ=λcsin2φ/2，变形后得Δλ/λc=sin2φ2，其中λc=2.43×10－12 m，m0=9.1×10－31 kg，c=3×108 m/s，

得到康普顿散射光子的波长增量与康普顿波长的倍数，即增长率（Δλ/λc）随着散射角的变化如图5所示.

图5的横坐标表示散射角φ，单位为度.纵坐标定义为Δλ/λc，是散射光子的波长增量的增长率，是一个比值，没有单位.由图可以看出波长的改变量的增长率随散射角的增加而增加.当φ=0时，波长不变，φ 增大时，λ－λ0也随之增加.这个结论和图2康普顿散射与角度的关系所表示的实验结果一致.

康普顿散射中光子波长变长的原因是：光子与自由电子发生碰撞时要损失一部分能量，光子自身能量的变小而导致频率降低，从而波长增大.对于相对原子质量大的物质来说，重原子中内层电子束缚很紧，所以康普顿散射效应较弱；而相对原子质量小的物质康普顿散射效应则较显著，这也是散射物质选取轻质物体的原因.

在光子与原子中的内层电子碰撞过程中，由于内层电子被原子束缚得比较紧，光子将和整个原子发生碰撞，原子的质量较大，碰撞以后光子能量损失就较少，波长不会有显著的改变，所以散射中有原入射波长的光.

结合式（6），代入已知条件 λc，m0，c，λ0/λc，编写程序得康普顿散射中反冲电子获得的能量增长率ΔE/m0c2随着散射角的变化规律如图6所示；同理结合式（9），代入已知条件，编写程序得反冲电子的动量增长率p/m0c 随着散射角的变化规律见图7所示.

图6反映出康普顿散射中反冲电子获得能量增长率随散射角的变化规律.在散射角度很小时能量增长率变化不明显，随着散射角度的增加反冲电子获得的能量增长率逐渐增大.在散射角一定的情况下，能量增长量率则随入射光波长的减小而增加.这是因为入射光波长越短，其能量越高，散射后传递给电子的能量越多.

图7反映出反冲电子的动量增长率随散射角的变化规律.与反冲电子获得能量增长率随散射角的变化规律相似，在散射角度很小时动量增长率变化不明显，随着散射角度的增加反冲电子获得的动量增长率逐渐增大；在散射角一定的情况下，动量增长率则随入射光波长的减小而增加.比较图6和图7可以看出，与反冲电子的能量增长率随角度的变化相比较反冲电子的动量增长率随角度的变化表现得更为明显和剧烈.

4康普顿散射实验的意义

康普顿效应中，光子和电子的相互作用是通过一个中间过程相联系的.量子力学表明，光子和电子之间的相互作用是通过“场量子”实现.这里面有两种方式，一种是自由电子先整体吸收光子，然后再释放出一个散射光子；另一种是自由电子先放出一个散射光子，再吸收入射光子.无论以哪种方式，光子都是以完整的单元产生或吸收［7］.通过康普顿散射实验的研究，可以看出：康普顿效应中的电子不像光电效应那样吸收光子，而是散射光子.因为自由电子若是吸收光子，就无法同时满足能量守恒和动量守恒.若自由电子吸收光子，同时考虑能量和动量守恒，以及相对论效应，则应有下面式子：

hυ0+m0c2=mc2" （10a）

hυ0ce→0=mve→0 （10b）

m=m01－v2c2 （10c）

由（10 a）的两边同除以c得：hυ0c+m0c=mc ，将（10 b）代入得 mv+m0c=mc，通过整理得：m0c=m（c－v），得m0=m（c－v）c，代入（10c）得：m（c－v）c=m1－v2c2，整理得到，1－vc=1－v2c2，要使等式成立，v=c，则实验就观察不出波长的变化，这与康普顿散射实验相违背.所以自由电子不可能吸收光子，只能散射光子.

我国物理学家吴有训1921年起协助导师康普顿作X射线散射光谱的研究工作，他从实验中得到的关于十五种不同元素的X射线散射谱图，这对证实康普顿效应普遍性作出了卓有成效的贡献，康普顿于1927年获得诺贝尔物理学奖.在量子物理教学中，介绍关于吴老在康普顿效应中的贡献，能够激发和鼓舞学生在量子物理的学习中，遇到困难时要有勇于克服困难的信心，具有一定的科学教育意义.

5结语

本文首先介绍了光电效应和康普顿散射实验的异同，对康普顿碰撞进行了详细的理论推导，并基于MATLAB对康普顿散射进行可视化研究.该研究可以增强学生对光子与微观粒子之间相互作用的理解，并澄清康普顿散射过程中的一些错误理解，使学生直观感受康普顿散射的物理本质特征.

［参考文献］

［1］杨军，蒋开明，葛传楠，武文远.康普顿效应教学中几个问题的探析［J］.大学物理，2009，28（11）：25-28.

［2］陈昌永，李韶华.康普顿效应与光子任意分割［J］.娄底师专学报，2000（4）：61-62.

［3］代波.康普顿效应的进一步讨论［J］.大学物理，2010，29（9）：30-32.

［4］COMPTON A H.A quantum theory of the scattering of X-rays by light elements［J］.Physical Review，1923，21（5）：483-502.

［5］COMPTON A H.The spectrum of scattered X-rays［J］.Physical Review，1923，21（5）：409-413.

［6］赵凯华，罗蔚茵.新概念物理教程：量子物理［M］.北京：高等教育出版社，2001：17-18.

［7］张三慧.大学物理学：量子物理［M］.2版.北京：清华大学出版社，2000：19-20.

［责任编辑赵小侠］