构造函数证明一个猜想不等式
2024-06-11陈宇
中学数学研究 2024年6期
陈宇
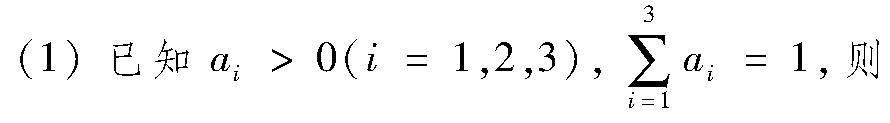
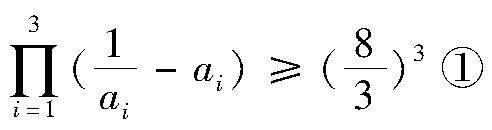
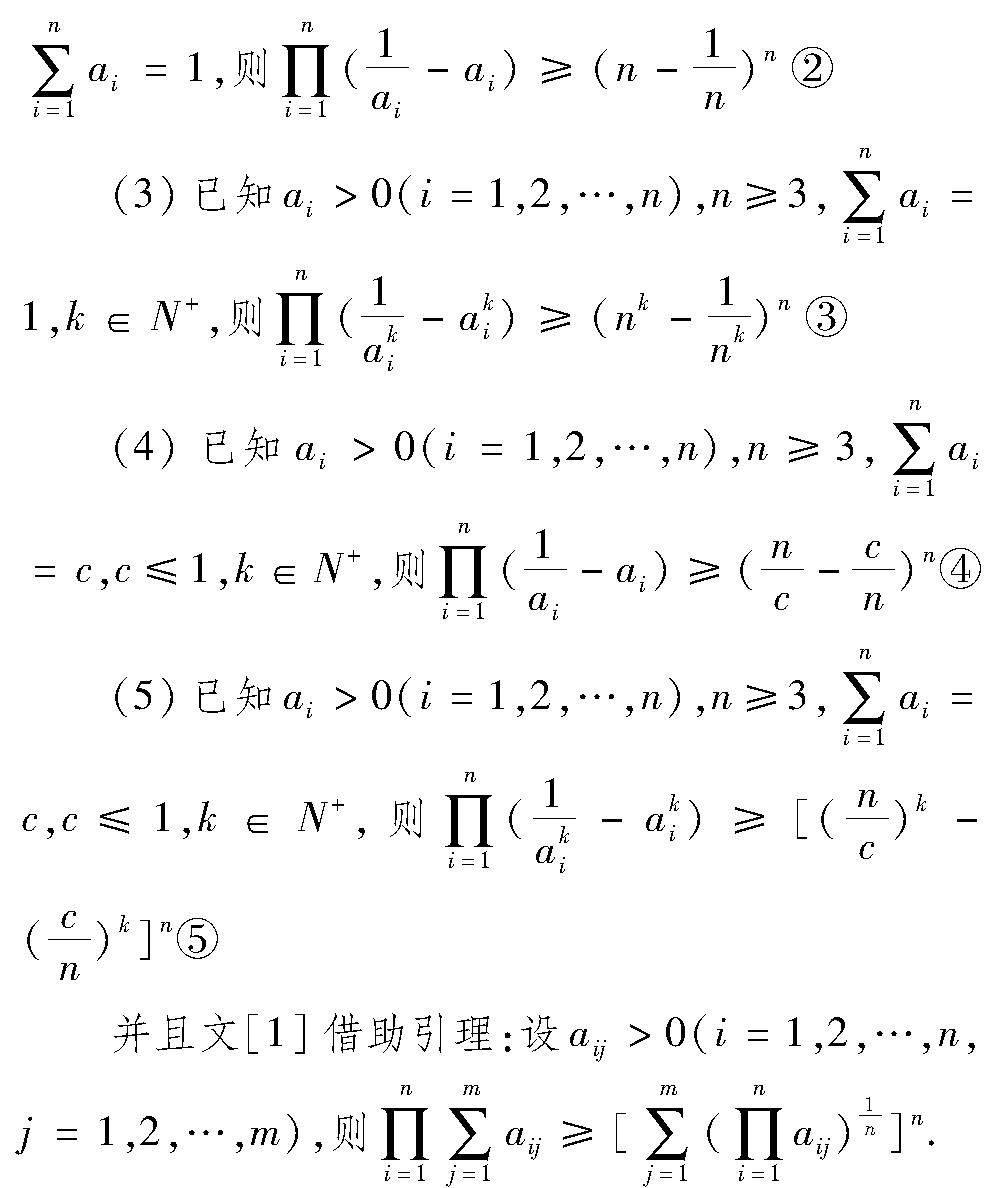
文[1]依次介绍了两组对稱不等式:
(2)已知ai>0(i=1,2,…,n),n≥3,
证明不等式⑤成立—结论:“⑤是①,②,③,④的统一推广”.进而给出.
笔者在此将通过构造函数证明此猜想成立.
当c=1时,不等式⑩即为不等式⑨;
当c=1,n=2,p=m,q=n时,令a1=a,a2=b,不等式⑩即为不等式⑧.
可见,不等式⑩是不等式⑥,⑦,⑧⑨的统一.
进而,当p=q=k时,不等式⑩即为不等式⑤.此时不等式⑩也是不等式①,②,③④的统一.
至此,不等式⑤,⑨所对应的两组不等式完美的统一于不等式⑩.
当然,本文之证法也可以看作不等式⑤(当p=q=k时),⑨的别证.
参考文献
[1]庞良绪.一个三元对称不等式的再推广[J],中学数学研究(江西师大),2023,9.
