以计数单位为核心 感悟运算的一致性
2024-06-04吕立峰
□吕立峰
《义务教育数学课程标准(2022 年版)》(以下简称 “2022年版课标” )指出,核心素养具有整体性和一致性。聚焦到 “数与运算” 主题,如整数、小数和分数的教学,即不仅要强调 “意义和关系的一致性” ,更要注重 “算理和算法的一致性” 。其中,前者在各版数学课程标准及配套的教材中均有所体现,只不过直到2022年版课标颁布才首次明确并重点强调了这一点。后者则是2022年版课标提出的一种全新的关系称谓,要求教师在课堂实践中进行更加深入的探索。
那么,在一致性视角下,如何对整数、小数和分数的四则运算教学进行整体设计呢?从数理逻辑的角度出发, “计数单位” 是贯穿四则运算一致性的核心概念。然而,在不同运算的教学中, “计数单位” 所发挥的功能和作用也各不相同。因此,在实际课堂教学中,教师需要灵活调整 “计数单位” 的应用视角,确保教学的深入与全面。
一、掌握加减运算的一致性:经历相同计数单位的数的加减运算
要使学生感悟到整数、小数和分数加减运算的一致性,关键在于引导他们经历相同计数单位的数的加减运算过程。在加减运算中,学生最先学习整数加减法,在此基础上学习小数加减法和分数加减法。按照这一学习顺序,学生很容易就能明白小数加减法的计算法则,本质上就是在执行相同计数单位的数的加减运算。然而,理解分数加减法的计算法则却并不容易。分数加减法的计算法则强调 “同分母分数相加减,分母不变,只把分子相加减;异分母分数相加减,先通分,再按照同分母分数加减法进行计算” 。从字面上来看,这与整数、小数加减法的计算法则存在显著差异。为了突破这一难点,教师应精心设计教学活动,建立分数加减法与整数、小数加减法之间的内在联系,引导学生体会各类加减运算本质上的一致性。
【教学片段1】 “整数、小数和分数加减运算” 教学
1.学生完成习题,提供研究素材(如表1)。

表1 学生计算整数、小数和分数加减情况
2.教师启发引导,沟通运算算理。
师:整数、小数和分数加减运算有什么相同点?
生:整数、小数加减运算时,都要把相同数位对齐,也就是让相同计数单位的数进行加减。
师:这个规则在分数加减法中也适用吗?
生:不可以,分数加减法的计算法则和整数、小数加减法的不同。
师:分数加减法的计算法则强调 “异分母分数相加减,先通分,再按照同分母分数加减法进行计算” 。这样的规定是基于什么原因呢?
生:这是因为异分母分数只有转化为同分母分数,它们的分数单位才能统一。
师:你能举例说明吗?
师:数学上, “分数单位” 是 “分数计数单位” 的简称,所以 “通分” 的过程实际上就是统一计数单位的过程。
生:我明白了!原来分数加减法和整数、小数加减法一样,都是将相同计数单位的数进行加减。
经过对上述教学片段的观察分析,可以确认学生的表现与课前预测相符。在面对整数和小数加减法时,学生能够准确地识别出它们的共同点。然而,当涉及分数加减法时,学生就会产生一定的困惑,因为分数加减法与整数、小数加减法在计算法则的表述上存在显著差异。为了帮助学生理解这一问题,教师在课堂上要利用有效的追问,清晰地向学生解释把异分母分数转化为同分母分数进行加减的原因,即实现计数单位的统一。计数单位统一之后,计算过程就会简化为 “分子相加减” ,也就是求相同计数单位的个数。通过这样的教学过程,教师成功地建立了分数加减法与整数、小数加减法之间的内在联系,使学生深刻感悟到加减法运算的一致性。
二、感悟乘法运算的一致性:经历因数相乘产生新的计数单位的过程
要使学生感悟到整数、小数和分数乘法运算内在的一致性,关键在于引导他们经历因数相乘产生新的计数单位的过程。 “产生新的计数单位” 从表述上来说可能较为新颖,但它在实际教学中的运用并不少见。比如,小数乘法的计算法则中提到 “看因数中一共有几位小数,就从积的右边起数出几位,点上小数点” ,其中 “点上小数点” 的过程就是产生 “新的计数单位” 的过程。分数乘法的计算法则中也提到 “用分子相乘的积作分子,用分母相乘的积作分母” ,其中 “用分母相乘的积作分母” 的过程也是产生 “新的计数单位” 的过程。那么,在一致性视角下,乘法运算教学应如何让学生体会到因数相乘会产生 “新的计数单位” 呢?
【教学片段2】 “小数乘小数运算” 教学
1.教师出示例题,让学生笔算0.8×0.3。
2.展示算法,聚焦重点。学生展示多种算法(略),重点研究列竖式解答的方法(如图1)。
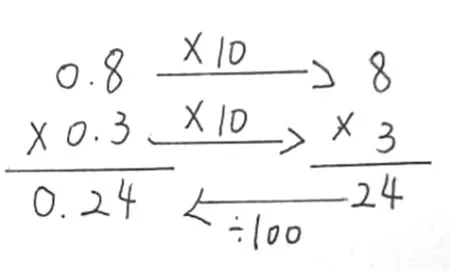
图1 0.8×0.3的竖式解答过程
生:两个因数0.8 和0.3 分别扩大到原来的10倍,它们的积就会扩大到原来的100倍。根据积的变化规律,只有把24 缩小到原来的,才能得到正确的积。
生:可以通过画图来说明。如图(a)所示,把正方形看作单位 “1” ,并在其中用阴影分别表示0.8和0.3。相当于把单位 “1” 平均分成100 份,每份是0.01。而两个阴影的重叠部分正好占其中的24份,也就是有24个0.01,即0.24。
师:这位同学的意思是,0.8表示8个0.1,0.3表示3 个0.1, “0.8×0.3” 的结果会产生一个新的计数单位0.01。这个新的计数单位是由两个因数的计数单位相乘得到的,即0.1×0.1=0.01。而把 “0.8×0.3” 看成 “8×3” 计算出的 “24” ,就表示新计数单位的个数。
[教师边解释算理,边把学生的图式补充完整,如图2(b)所示]
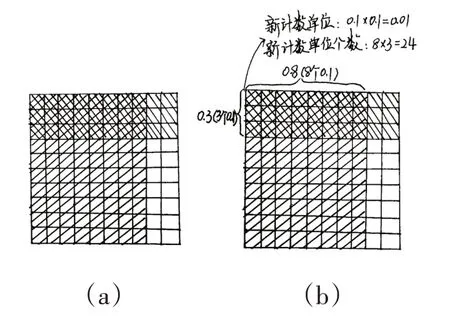
图2 0.8×0.3的图式表征过程
3.归纳算法,理解本质。
师:通过刚才的学习,我们知道了小数乘法的计算法则是 “先把小数乘法转化成整数乘法计算,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点” 。现在,你们明白这个法则的意思了吗?
生:计算法则中, “把小数乘法转化成整数乘法计算” 得到的积就是 “新计数单位的个数” , “看因数中一共有几位小数” 能确定积的计数单位,而积的计数单位就是 “两个因数的计数单位相乘之后产生的新计数单位” 。
【教学片段3】 “分数乘分数运算” 教学
2.展示算法,聚焦重点。学生展示多种算法(略),重点研究用画图求积的方法,如图3(a)所示。
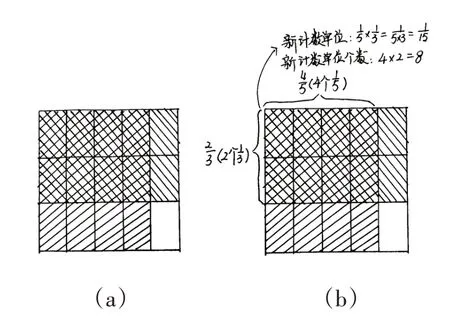
图3 ×的图式表征过程
师:大家能看懂这位同学的方法吗?
[教师边解释算理,边把学生的图式补充完整,如图3(b)所示]
3.揭示本质,归纳算法。
师:刚才的思考过程可以用怎样的算式记录呢?
师:那么,你们认为分数乘法的计算法则是什么呢?
生:用分子相乘的积作分子,用分母相乘的积作分母。
【教学片段4】 “乘法运算的复习和整理” 教学
1.教师整体呈现三类乘法算式。

整数乘法images/BZ_50_334_874_463_925.png小数乘法images/BZ_50_513_863_865_935.png分数乘法images/BZ_50_918_868_1153_930.png
2.围绕核心问题展开讨论:小数、分数乘法运算与整数乘法运算之间有什么关联?
3.经过师生间的深入交流与讨论,达成共识:小数和分数的乘法运算都会产生新的计数单位。若能够确定这个新计数单位,便能将小数和分数的乘法转化成整数乘法进行计算。
4.利用学习材料深入解析:比如0.2×0.4,两个因数的计数单位都是0.1,它们相乘就会产生新的计数单位0.01。又如两个因数的计数单位分别是它们相乘也会产生新的计数单位。一旦确定了积的计数单位,这两道题就能够转化成整数乘法 “2×4” 。教师根据学生的回答适时进行板书,如图4所示。

图4 乘法运算部分板书
上述三个教学片段构成了一个整体,呈现了乘法运算两个阶段的教学重点。第一个阶段聚焦于 “小数乘小数” 和 “分数乘分数” 的运算教学,主要通过数形结合,让学生经历两个因数相乘产生新计数单位的全过程。这两节课基本采用相同的教学思路,再辅以可视化的学习材料,使学生感悟到小数乘法和分数乘法运算的内在一致性。第二个阶段则是 “乘法运算的复习和整理” ,一方面通过对比和概括揭示了小数乘法和分数乘法运算的一致性,另一方面通过建立小数乘法、分数乘法与整数乘法的联系,消除了三者之间的隔阂,构建起乘法运算一致性的结构。
三、理解除法运算的一致性:经历高级计数单位不断细分的过程
要使学生感悟到整数、小数和分数除法运算的内在一致性,关键在于引导他们完整地经历高级计数单位不断细分的过程。在这个过程中,有三个关键的教学节点需特别关注。
第一个教学节点是 “两位数除以一位数的笔算除法,首位不能整除的情况” ,意在初步启发学生对高级计数单位细分方法的认识。现有教材在编写意图上已充分体现了这一点。如图5所示,人教版教材利用小棒直观辅助教学,使学生能够清晰地观察到 “1 个十” 细分为 “10 个一” 的过程。根据课堂观察,一线教师在此方面的执行力度值得肯定。
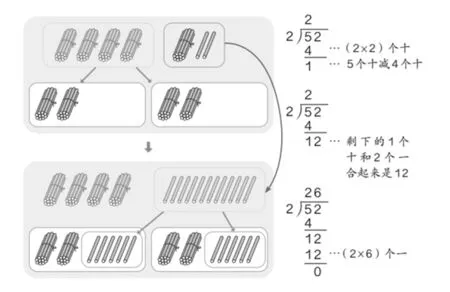
图5 人教版教材 “笔算除法”
第二个教学节点是 “除数是整数的小数除法” ,要求学生对高级计数单位细分的过程有更深的理解。然而,在当前教学实践中,许多教师倾向于直接传授计算法则,即 “除得的商有余数时,在余数末尾添0继续除” ,而忽视了计算法则背后的原理。
第三个教学节点是 “异分母分数除法” ,是对高级计数单位细分的拓展与深化。在这一环节,教师的做法与前述环节类似,多侧重计算法则的传授,即 “除以一个不为0 的数,等于乘这个数的倒数” ,而指向算理的教学目标则基本被淡化。那么,在一致性视角下,小数和分数除法的教学应如何让学生经历高级计数单位不断细分的全过程呢?
【教学片段5】 “除数是整数的小数除法运算” 教学
1.学生试做:86÷4(竖式中的前两次试商如图6所示)。
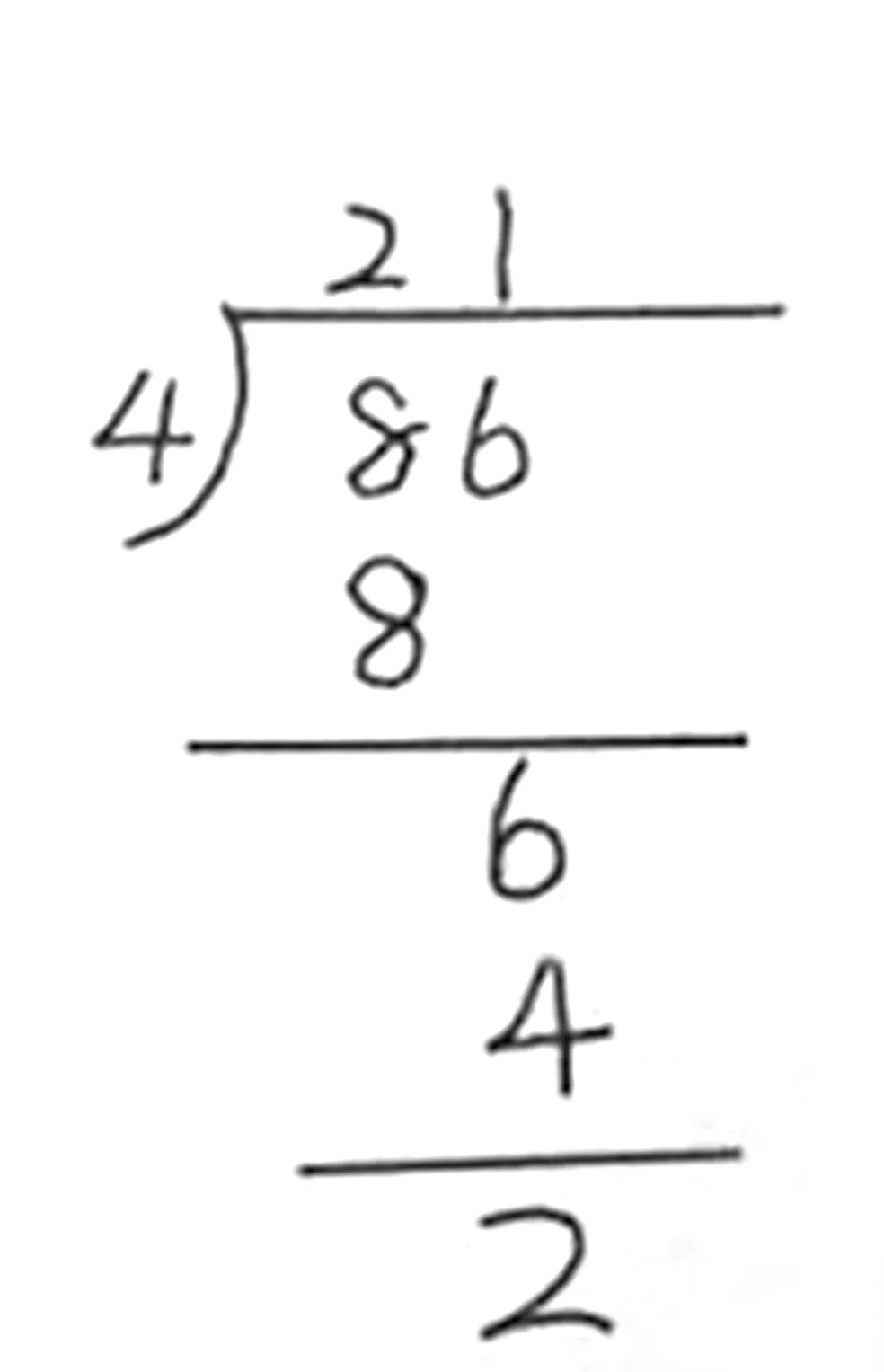
图6 86÷4的试商过程
2.难点揭示:在图6所示算式中,余数2不够除4怎么办?
3.策略思考:为了解决这个问题,可以在余数2的后面添 “0” ,继续进行除法运算。
4.明晰算理:余数2 表示2 个一。在其后面添加1个 “0” ,可以将2个 “一” 看作20个 “0.1” 。用20个0.1 除以4,商是5 个0.1,即0.5。为了正确表述结果,需要在21的后面点上小数点,再写5。
5.图式表征:如图7 所示,通过画图解释整个计算过程。
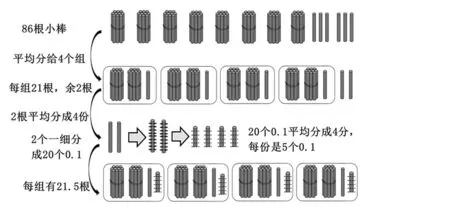
图7 “86÷4” 算理表征过程
6.教师总结提炼:在余数2 后面添加1 个 “0” ,表示将2 个一转化成20 个0.1,也就是把计数单位 “一” 细分成10个 “0.1” 。这种将 “高级计数单位” 细分成 “低级计数单位” 的做法,确保了小数除法运算的顺利进行。这与整数除法具有一致性。
【教学片段6】 “分数除以分数运算” 教学
2.理解多种算法。
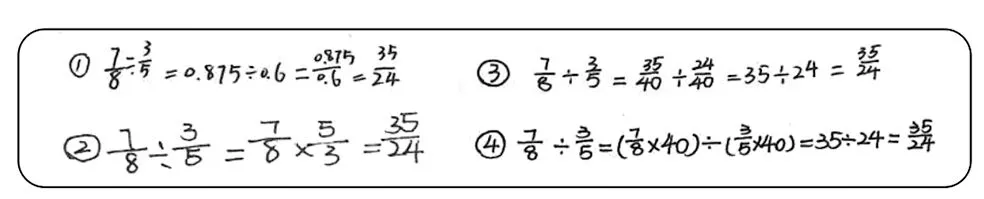
师:用方法③解答的同学是怎么思考的呢?
师:你能把这个过程用画图的方式表达清楚吗?
(师生合作,共同完成算理表征过程,如图8所示)
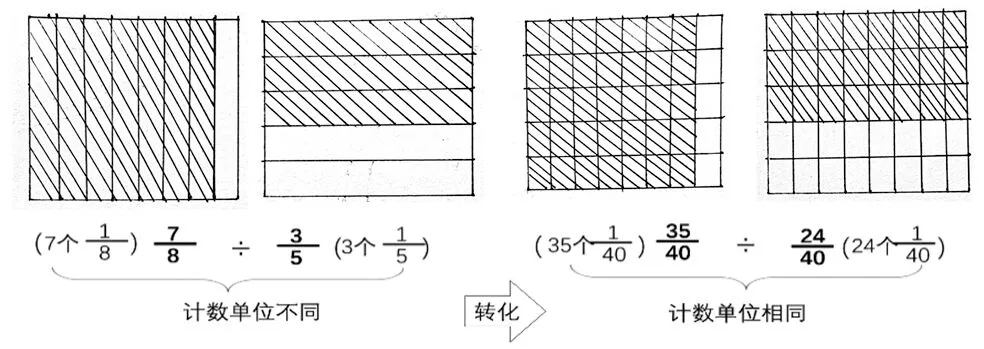
图8 “算法③” 算理表征过程
4.师生共同提炼算理:对于异分母分数的除法,可以先通分,将它们转化成同分母分数再相除。在这一过程中,对被除数和除数的计数单位进行细分是关键。当它们的计数单位相同时,分子相除的结果即为异分母分数相除的商。
【教学片段7】 “除法运算的复习和整理” 教学
1.整体呈现三类除法算式。
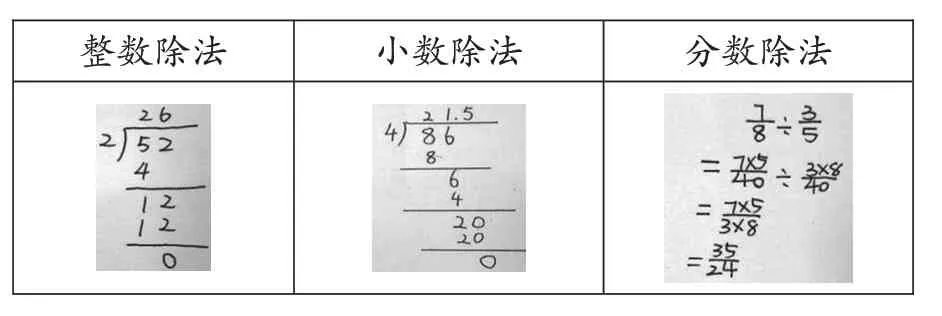
整数除法小数除法分数除法images/BZ_51_1369_2792_1482_2959.pngimages/BZ_51_1644_2792_1798_2959.pngimages/BZ_51_1936_2781_2125_2970.png
2.归纳算式的共性,理解运算的一致性。
教师提问: “整数、小数、分数三类除法运算有哪些共同之处?”
师生共同归纳:这三类除法运算在本质上是一致的。它们都涉及 “高级计数单位的细分” 过程,依靠计数单位的不断细分逐步推进。比如:在整数除法52÷2中,将余数1个 “十” 细分成10个 “一” ;在小数除法86÷4中,将余数2个 “一” 细分成20个 “0.1” ;在分数除法中,将7个和3个细分成教师根据学生的回答随机板书,如图9所示。
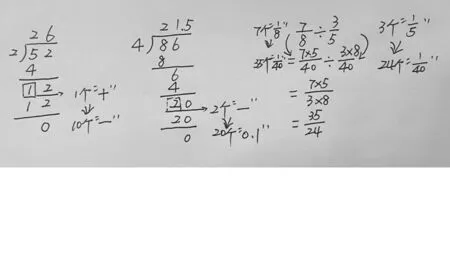
图9 三类除法计算题 “细分计数单位”
上述三个教学片段构成了一个逐步深入的整体。在 “除数是整数的小数除法运算” 的教学中,教师通过分小棒的直观演示,让学生看到计数单位不断细分后,两数相除的商既可以用整数表示,也可以用小数表示。在 “分数除以分数运算” 的教学中,教师同样借助形的直观,让学生看到从计数单位细分的角度出发,可以解释分数除法的计算法则。在 “除法运算的复习和整理” 的教学中,则通过对三类除法计算题共性的归纳,让学生理解计数单位细分是推进除法运算的关键,从而构建除法运算一致性的结构。
通过教学实践不难发现, “计数单位” 在打通四则运算一致性的过程中确实起到了至关重要的作用。为了进一步聚焦这一核心概念,需要对它及其相关问题进行深入探讨。
第一,如何使学生深刻理解 “计数单位” 这一概念? “计数单位” 是计算教学的核心概念,学生对它的理解程度将直接影响后续学习的效果。事实上,对计数单位的理解与 “数概念一致性” 的教学是密切相关的。例如, “3表示3个一,0.3表示3个0.1,表示3个” 等,就是从计数单位和计数单位的个数这个角度来认识整数、小数和分数的一致性的表现。因此,夯实 “数概念一致性” 的教学,可以帮助学生深刻理解 “计数单位” 这一概念,进而为感悟四则运算的一致性提供保证。
第二,用 “计数单位” 打通四则运算一致性的本原是什么?在回答这个问题前,可以先回顾一下四则运算一致性的具体表现:只要找到了相同的计数单位,小数和分数的加减法运算就可以将相同计数单位的数相加减的过程转化为一道整数加减法计算题;只要知道了因数相乘所产生的新计数单位,小数和分数的乘法运算就可以将求新计数单位个数的过程转化为一道整数乘法计算题;只要掌握了高级计数单位细分的方法,小数和分数的除法运算就可以将求商的过程转化为一道整数除法计算题。由此可见, “转化” 是用 “计数单位” 打通四则运算一致性的数学本原。
综上所述, “计数单位” 在感悟整数、小数和分数四则运算一致性的过程中发挥着关键作用。在 “数概念一致性” 的教学中,应突出 “计数单位” 的核心地位,加深学生对这一概念的理解。在 “数运算一致性” 的教学实践中,应以 “计数单位” 为内核,消除整数、小数和分数四则运算之间的隔阂,强调 “转化” 的数学思想。
