以核心问题为统领,上好数学拓展内容*
2024-06-04鲍善军
□鲍善军
《义务教育数学课程标准(2022 年版)》指出: “数学教材为学生的数学学习活动提供了学习主题、知识结构和基本线索,是实现数学课程目标、实施数学教学的重要资源。” 教材要 “编入介绍与教学内容相关的重要数学概念、思想方法等拓展性内容” 。因此,教师要基于数学教材内容,深度挖掘其价值意义,设计符合学生认知规律的数学拓展内容,这有助于加强学生对数学知识之间的关联性的理解,有助于开阔学生的认知视野,使学生在数学上获得更好的发展。
作为数学教学的重要组成部分,小学数学拓展内容可以涵盖对教材中某一重要数学概念的根源探究、对某一单元主题知识的扩充延伸研究、对特定学习重难点的深入挖掘开发,以及对某一数学思想方法的渗透与应用等。为实现此目标,数学拓展教学要聚焦核心内容,通过问题统领和任务驱动,为学生提供充足的探究空间。这有助于引导学生在解决问题的过程中,全面深入地理解一类问题,从而使课堂教学更为简约高效,加深学生对数学的理解,提升其数学思维水平。
一、在课堂观察中找准数学教学的问题
问题是数学的心脏,也是数学研究的起点与归宿。纵观教育历史,无论是孔子的 “启发式教学” 还是苏格拉底的 “产婆术” ,都突显了问题设置在教学中的重要性。然而,通过课堂观察可以发现,数学教师引领学生思考的问题质量普遍不高。具体表现在以下三个方面。
(一)多——问题琐碎,学生的思考空间不足
问题作为教学的载体,对推动学生思维发展具有重要作用。但从课堂观察来看,部分教师的课堂提问频次较高,一堂课中提出问题的数量多达四五十个,学生疲于应对。与此同时,问题的思维含量却不高。课堂气氛看似热闹,其实学生不需要经过太多思考,就能轻轻松松地进行解答。这样琐碎的问题设计,无法给予学生足够的思考空间,未能有效促进学生的思维发展,反而可能使他们滋生思维惰性。因此,教师需要重新审视和改进教学方式,以更好地培养学生的思维能力和创新精神。
(二)散——问题随意,知识的本质指向不明
著名科学家加波普尔提出:科学与知识的增长,永远始于问题。但在实际教学中,部分教师提问时较为随意,没有对问题进行科学的设计与组织,导致问题未能明确指向知识的本质。换言之,这些问题未能从深度和广度上充分揭示知识的内涵,问题之间也缺乏必要的逻辑联系。这导致学生尽管回答了许多问题,也很难形成清晰的知识体系。受此影响,教学很容易偏离既定目标,教学效果自然不尽如人意。
(三)浅——问题封闭,难以引发深度思考
思维源自问题,好的问题能引发学生的深度思考。但在实际教学中,部分教师对教材内容缺乏深入研读,提出的问题往往浮于表面,难以引发学生的深度思考。这种封闭式的问题,忽略了知识内容之间的内在关联,不利于学生形成对知识的整体性建构。而就题论题的提问方式,又忽视了教材所蕴含的深层次价值,导致学生的学习碎片化、浅层化,无法为后续的深入学习提供有力支持。
上述现象反映出当前数学拓展教学在提炼 “核心问题” 和思考 “适切问题” 方面存在不足。为此,笔者所在团队积极探索研究以核心问题为统领的拓展教学。一方面立足当下的课堂学习,帮助学生更好地获得 “四基” ,发展 “四能” ;另一方面着眼于学生未来的素养发展,培养学生的科学精神,包括质疑问难、自我反思和勇于探索等思维品质。
二、以核心问题为统领的数学拓展教学设计
张奠宙教授提出,数学教学原则可以概括为学习数学化原则、适度形式化原则、问题驱动原则和渗透数学思想方法原则。 “核心问题” 可依据以上原则确立。教师在深入研究教材的基础上,紧扣教学内容和目标,精心构建一系列既相互独立又相互关联的核心问题,进而形成具有内在逻辑性与整体性的问题链。以核心问题为统领的数学拓展教学,旨在激发学生的认知冲突,引导他们主动探究、体验和理解数学本质,从而实现数学知识的系统构建及数学能力的全面提升。
小学数学拓展教学以 “学为中心” 理念为指导,聚焦核心内容,从中提炼出一系列核心问题。在此基础上,又将每个核心问题进一步细化为若干驱动性子问题。由此整体推进学生对核心内容的深入探究,全面达成拓展教学所设定的教学目标(如图1)。
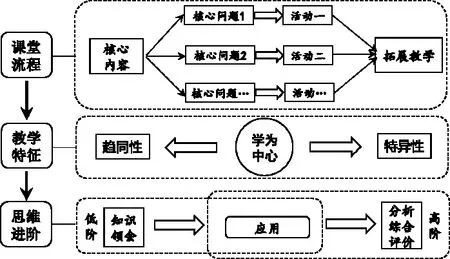
图1 以核心问题为统领的数学拓展教学框架
数学拓展教学具有趋同性与特异性。趋同性强调从低起点出发,通过不断努力,逐步走向深度学习。特异性则重视学生间的个体差异,旨在促使不同学生实现各自在数学上的发展。这种拓展教学有助于推动学生的思维水平从低阶的领会水平迈向应用水平,进而跃至高阶的分析、综合与评价水平,实现学生思维能力的进阶与核心素养的发展。
三、以核心问题为统领的数学拓展教学策略
以核心问题为统领的数学拓展教学需要深度挖掘核心内容所蕴含的价值与意义,以核心问题链为基本脉络构建学与教的基本框架,使学生在经历 “结构化、层进式、可持续” 的问题解决过程中,不断深化对数学的理解,逐步提高思维水平。
(一)提炼核心问题,从问题走向问题链
核心问题是指针对教学目标和重难点所提出的关键问题。它不仅指向知识的本质,还具备提纲挈领的作用。可见,核心问题是学生思考的脚手架、知识学习的大纲。每个核心问题都能形成一个学习板块,并通过细化拆分,形成一节课或某一环节的 “问题链” 。这种链式结构有助于学生深入理解知识,实现知识的整体建构。
1.精准确定核心内容,设计核心问题主链
为确保问题具有针对性,教师需要深入研究教材,通过纵向梳理和横向对比,清晰掌握教材的编排体系与编排意图,并结合学生实际情况,精准把握其学习起点和学习时可能存在的疑点与盲点。
例如, “正方形数的学问” 教学的核心内容为正方形数,包括 “以数表形” 和 “以形验数” 两个方面。据此,笔者设计了以下三个核心问题。
核心问题1:什么是正方形数?
核心问题2:正方形数有什么变化规律?
核心问题3:正方形数之间有什么关系?
这三个核心问题是基于正方形数这一核心内容设计的,既具有思考空间,又层层递进,有助于学生认识学习正方形数的意义以及知识间的联系。
2.形成子问题链,构建完整的问题链框架
问题链是教学思路的具体体现,具有较强的可操作性。设计问题链时,一般要遵循从整体到局部的原则,先构建统领整节课的主问题链,再将每个核心问题进行拆解,形成各环节的子问题链。
例如,在 “正方形数的学问” 教学中,核心问题2 “正方形数有什么变化规律?” 起着承上启下的作用。它既是对核心问题1 “什么是正方形数?” 的进一步深化,也是后续探究核心问题3 “正方形数之间有什么关系?” 的基础。因此,笔者从学生的角度出发,将核心问题2具体化为: “一个正方形数,至少增加多少才能成为一个新的正方形数?” 并在此基础上,将其进一步细化拆解为以下三个子问题。
子问题1:正方形数 “1” 至少需要加几才能成为一个新的正方形数?
子问题2:这个数继续加几,又能形成一个新的正方形数?
子问题3:从中你们发现什么规律?
这三个子问题驱动学生的数学活动逐步深入,不仅决定了一节课的走向,还映射了学生的学习路径。
3.梳理问题序列,优化问题链设计
构建问题链框架后,教师需认真分析与研判以下几个问题:问题链的逻辑性是否符合问题解决过程的逻辑结构?问题链的整体性是否与数学学科体系结构保持一致?每一个问题本身是否符合科学性、清晰性和合理性的要求?以便学生能够明确理解问题的本质和求解的方向。在此基础上,教师梳理问题序列,优化完善问题设计,使问题链更具策略性与可操作性,在内容上层层深入,在思维上实现进阶。
以 “正方形数” 的教学环节为例,教师通过分析拆解核心问题,精心预设子问题链,构建了完整的问题链框架(如图2)。
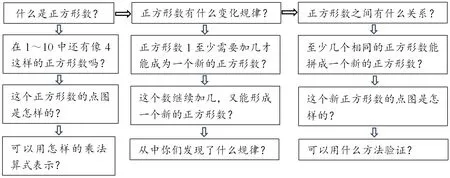
图2 “正方形数” 问题链框架
在这一问题链构架中,横向的核心问题紧扣 “正方形数” 这一核心内容,形成具有较大思考空间的主问题链;纵向的子问题链则助力学生实现结构化学习,促进知识体系的整体建构。
(二)关注不同类型的问题链,引领学生思维发展
教育的本质是培养思维,培养思维的最好场所是课堂。教师需要整体把握教学内容的本质和结构,通过提炼核心问题,设置问题链,引导学生进行独立思考、动手实践、自主探索以及合作交流。这样的教学方式能够促进学生的深度学习,推动其思维向更深层次、更广层面、更灵活的方向发展,从而使学生学会运用数学的思维方式来思考和解决现实问题。
1.递进式问题链:由浅入深,推进学生思维的深度
递进式问题链是依据事物之间的内在联系,通过正向或逆向思维方式设计的层层递进的问题串,各问题之间具有严密的逻辑性和层次性。在递进式问题链的引导下,学生对问题的思考逐步深入,思维的深刻性获得提升。
例如, “乘积最大的秘密” 教学的核心问题依次为:①两位数乘两位数的乘积最大是多少?②三位数乘两位数的乘积最大是多少?③多位数乘多位数的乘积最大是多少?(如图3)这三个问题由浅入深,逐步引领学生探究乘积最大的秘密。学生则在依次解决这些问题的过程中,不断加深对乘法意义本质的理解。这样的探究过程拓展了知识的外延,促使学生的思维不断向深处延伸,提升了学生解决问题的能力。
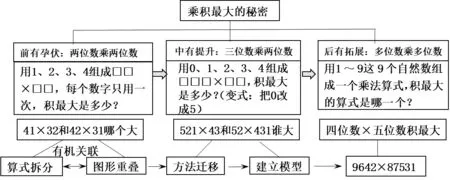
图3 “乘积最大的秘密” 教学框架
2.并列式问题链:由聚到散,拓宽学生思维的广度
思维的条理性源于问题的结构化。教师要引导学生对模糊、无序的问题进行梳理与提炼,明晰教学内容之间的联系与区别,形成结构化的并列式问题链,从而使学生思考问题的角度更加全面、路径更加清晰。
例如,在教学 “折线统计图的再认识” 时,教师对教材中的相关练习题进行梳理,从中提炼出指向概念本质的并列式问题链(如表1)。由此驱动学生展开自主探究,帮助学生将原本孤立的知识点融合在一起,形成一个纵横交错、脉络清晰的思维结构,从而拓宽学生思维的广度。

表1 “折线统计图的再认识” 问题链设计
在这一问题链的指导下,学生将折线统计图与条形统计图进行关联,从而在图形的选择、信息的对比以及数据的分析中,逐步明确 “离散数据” 与 “连续数据” 之间的根本区别,不断提升自身的认知能力,完善自身的认知结构,进而逐步建立结构化的思维模式。
3.迁移式问题链:由此及彼,提升学生思维的灵活度
学生的学习过程就是在原有知识基础上不断扩展和深化的过程。这就要求教师必须紧密结合学生的既有经验和认知结构设计迁移式问题链,引领学生摆脱思维定式,激发创新思维,从而生成新问题、形成新思考、获得新发现,由此及彼,提升思维的灵活度。
例如,学生在五年级上册学习了 “小数乘法” 和 “小数除法” 之后,能依据加减乘除的运算意义列出算式,并根据算法进行小数四则运算,但对于四则运算之间的内在联系和一致性,却缺乏深入的理解。为此,笔者进行了 “小数四则运算的再认识” 教学研究。首先,引导学生探究 “小数加减法之间有什么联系” ,帮助他们认识小数加减法算理的一致性,即求 “有几个相同的计数单位” 。其次,引导学生借助猜想、验证、辨析等数学活动,发现小数乘法同样是在求 “有几个相同的计数单位” ,但计数单位会发生变化,从而深入感悟小数乘法计数单位变化的内在逻辑。最后,引导学生进行迁移思考:小数除法还是求 “有几个相同的计数单位” 吗?在这一系列对小数四则运算的关联与比较中,学生感悟到数的运算以及运算之间的关系,体会到数的运算本质上的一致性,发展了结构化思维,提升了运算能力和推理意识。
数学拓展教学注重培养学生的关联性理解、概括性思维、批判性思维和创新性思维等高级思维能力。教学时,教师借助问题链,引导学生开展比较、归纳、迁移等思维活动,由此不断拓展和延伸其思维 “触角” ,使其实现思维能力的进阶和提升。
(三)依托问题链,展开 “板块推进” 式教学
佐藤学教授提出:课程设计越简单越好,如果要点过多,教师往往会专注于自己是否达成目标,而忽略了孩子的反应。因此,实施问题链驱动策略的关键在于提炼出核心问题,以核心问题构成学习活动的基本板块,再通过各个子问题链驱动学生进行深度思考和全面探究,从而促进学生学习的真正发生。这样的教学摒弃了传统 “线性串联” 的教学方式,转向 “板块推进” 的探究方式,使课堂不再受到固定流程的束缚,而是展现出更为丰富多元的过程。
综上,以核心问题为统领的数学拓展教学,能有效解决当前课堂中教师提问多、散、浅,学习活动缺乏聚焦、逻辑不强、深度不足等问题。既有助于教师明确学习主线,简化课堂教学,又有助于学生聚焦学习主题,深化数学理解,理清学习思路,提升思维水平。不过,在实施拓展教学策略的过程中,也会遇到一些新的挑战。这就要求教师根据数学学习内容的特性和学生思维的特点,精准把握核心问题,明确教学的主次关系,以高屋建瓴的姿态,引导学生进行深入思考、自主探究和主动建构,逐步学会用数学的眼光观察、用数学的思维思考、用数学的语言表达。
