面向可打击区域的高超声速飞行器制导控制一体化方法研究

赵良玉 时皓铭 王建华 崔磊

摘 要：针对高超声速飞行器制导和控制系统分离设计方法的不足， 提出通过制导控制一体化设计提升其可打击区域的方法。 首先， 在建立高超声速制导控制一体化模型的基础上， 揭示了其通过控制弹体坐标系与地面坐标系的牵连加速度来跟踪制导指令的工作原理。 其次， 通过典型弹道的数值仿真， 对比分析了制导控制一体化设计相较于分离设计的控制信号差异。 最后， 通过确定制导控制分离设计及一体化设计的高超声速飞行器可打击区域的方式， 从大样本仿真角度体现制导控制一体化的优势。 结果表明， 制导控制一体化设计可以放宽对可用过载的需求且有助于提升高超声飞行器的可打击区域。

关键词：  制导控制一体化； 大样本仿真； 可打击区域； 高超声速飞行器； 过载约束

中图分类号：TJ765

文献标识码： A

文章编号：  1673-5048（2024）02-0091-08

DOI： 10.12132/ISSN.1673-5048.2024.0057

0 引  言

高超声速飞行器具有飞行速度高、 航程远等特点， 相比传统弹道导弹末端打击时间更短、 机动能力更强， 在现代战争中的地位愈发重要［1］。 然而， 高超声速飞行器的制导控制系统设计面临强耦合、 强非线性、 快时变等复杂问题［2］， 使得基于时标分离假设分别独立设计制导系统和控制系统的传统方法， 在面对高超声速飞行器这类复杂被控系统时具有较强的局限性［3］。 与制导控制分离设计的理念不同， 制导控制一体化以攻角、 侧滑角、 倾侧角为“桥梁”， 建立制导系统与控制系统的联系， 充分考虑二者耦合作用产生执行机构的控制指令［4］。

目前， 制导控制一体化的研究成果主要分为方法研究和模型建构两个方面。 常用的制导控制一体化方法包括滑模控制、 反步设计、 自适应控制等［5］。 在滑模控制方法的研究方面， Ming等［6］基于非奇异终端滑模控制方法设计了含有扩张状态观测器的制导控制一体化系统， 在未知目标机动和气动系数的情况下具有较好的鲁棒性。 Li等［7］提出了一种基于全局终端滑模控制的制导控制一体化方法， 可以确保系统状态的快速收敛。 文献［8］使用滑模控制方法和非线性有限时间扰动观测器构建了一种攻击时间约束的制导控制一体化系统， 数值仿真表明其能够在满足时间约束的情况下命中移动目标。 文献［9］提出了分数积分终端滑模控制的制导控制一体化方案， 在满足攻击角度约束的情况下具有较好的鲁棒性。 文献［10］提出了一种考虑了攻击角度约束和执行器饱和的制导控制一体化方法， 超扭转状态观测器和滑模控制的结合可以保证该方法对扰动和目标加速度具有很强的鲁棒性。

在反步设计方法的研究方面， Chao等［11］设计了一种全局有限时间稳定的制导控制一体化方法， 对非匹配不确定性和参数不确定性均具有较强的鲁棒性。 Chang等［12］提出了一种基于状态观测器、 自适应增量反步控制的制导控制一体化方案， 数值仿真表明其能够命中机动

目标， 具有较好的弹道性能。

在自适应控制的研究方面， 文献［13］设计了一种自适应参数的制导控制一体化方法， 可以保证闭环系统有限时间收敛。 文献［14］通过引入四阶势垒李雅普诺夫函数， 使得自适应制导控制一体化方法可以在随机干扰和未知目标机动的情况下满足全状态约束条件。 文献［15］设计了一种多约束自适应有限时间的制导控制一体化系统， 数值仿真验证了其对初始状态偏差和气动参数不确定性的鲁棒性。 文献［16］设计了一种基于非线性自适应滑模控制的制导控制一体化方法， 一定程度克服了反步設计方法的时滞问题， 提升了一体化程度。

同时也有学者研究了常见约束条件下的制导控制一体化方法， Liu等［17］利用势垒李雅普诺夫函数构建了考虑输入饱和的制导控制一体化方法， 该方法保证了闭环系统中信号的一致最终有界。 Fu等［18］设计了一种有限时间收敛的制导控制一体化方案， 能够满足攻击角度约束， 避免舵偏角出现饱和。 Tian等［19］设计了一种考虑导引头视场约束的制导控制一体化方法， 数值仿真表明其能够保证导引头对目标的持续锁定。 Zhao等［20］利用神经网络观测器估计不确定性， 设计了一种考虑视场角约束的制导控制一体化方法， 数值仿真表明其既能保证系统状态的有界性又能在视场角约束下命中目标。 Bao等［21-22］针对高超声速变翼展导弹， 利用自适应反步控制设计了一种满足攻击角度的制导控制一体化方法， 利用机翼的变翼展特性实现翼展和攻角的协同变化， 实现了快速稳定控制效果。 Liu等［23］针对执行器故障问题提出了一种基于势垒李雅普诺夫函数和自适应控制的制导控制一体化方法， 可以在执行器故障、 建模误差、 气动参数摄动的情况下保证闭环信号的有界。

在模型建构方面， Wang等［24］提出了一种制导控制一体化降阶模型， 相比于分离设计的制导控制模型提升了集成度［25］。 文献［26］提出了一种全集成的制导控制一体化方法， 该方法利用加速度分量到舵偏角的解析模型进一步提升了制导控制一体化的程度， 数值仿真验证了其有效性和鲁棒性。

在方法研究方面， 现有的研究成果多注重于对所提出方法的稳定性进行证明， 往往缺少对制导控制一体化工作机理的探究； 在模型建构方面， 现有的研究成果多采用单条弹道的数值仿真与其他方法对比， 缺少从控制信号角度分析一体化的机理； 且在上述两个方面的研究几乎没有从大样本仿真的角度体现制导控制一体化的优势。 为此， 本文以典型高超声速飞行器的制导控制模型为基础， 通过对制导控制一体化工作原理的探析及不同约束条件下的大样本仿真， 分析制导控制一体化控制信号的生成过程且证明制导控制一体化设计方法在提升高超声速飞行器可打击区域、 放宽约束限制等方面的优势。

1 飞行器制导控制模型

1.1 分离设计制导控制模型

以文献［24］中适用于侧滑转弯（Skid To Turn， STT）模式的高超声速飞行器分离式设计制导控制模型为例， 其具有三层控制环路的结构如式（1）所示。 弹道倾角和弹道偏角的控制输入为升力、 侧向力（与攻角、 侧滑角直接相关的量）； 攻角、 侧滑角、 倾侧角的控制输入为三通道角速率， 三通道角速率的控制输入为气动力矩（与舵偏角直接相关的量）。

θ·

σ·=

－gcosθV－1

0+

m－1V－10

0－m－1V－1secθ

LC

α·β·υ·=

－cosαtanβsinαtanβ1

sinαcosα0

cosαsecβ－sinαsecβ0

ωxωyωz+Tθσ

σ·θ·

ω·xω·y

ω·z=－J－1xx（Jzz－Jyy）ωzωy

－J－1yy（Jxx－Jzz）ωxωz

－J－1zz（Jyy－Jxx）ωyωx+

J－1xx000J－1yy000J－1zz

MxMyMz（1）

式中： θ、 σ分别为弹道倾角、 弹道偏角； g为重力加速度； V为速度大小； m为飞行器质量； L、 C分别为气动升力和气动侧向力； α、 β、 υ分别为攻角、 侧滑角、 倾侧角； ωx、 ωy、 ωz分别为三通道角速率在弹体坐标系的分量； Jxx、 Jyy、 Jzz分别为飞行器绕惯性主轴的转动惯量； Mx、 My、 Mz分别为气动力矩在弹体坐标系的分量； 矩阵Tθσ的表达式为

Tθσ=sinυcosθsecβ－cosυsecβ

－cosυcosθ－sinυ

－sinυcosθtanβ－sinθcosυtanβ。

1.2 制导控制一体化模型

制导控制一体化模型采用文献［25］中的两层控制环路， 其结构如式（2）所示， 借助于弹体坐标系的加速度信息， 弹道坐标系的加速度控制输入为三通道角速率， 三通道角速率的控制输入为气动力矩（与舵偏角直接相关的量）。

TOHaxhayhazh

=B·Cωxωyωz+TOBu·v·w·

ω·xω·yω·z=

－J－1xx（Jzz－Jyy）ωzωy－J－1yy（Jxx－Jzz）ωxωz－J－1zz（Jyy－Jxx）ωyωx+J－1xx000J－1yy000J－1zzMxMyMz（2）

式中： TOH为弹道坐标系到地面坐标系的旋转矩阵； axh、 ayh、 azh分别为加速度指令在弹道坐标系的分量； TOB为弹体坐标系到地面坐标系的旋转矩阵； u、 v、 w分别为速度在弹体坐标系的分量； u·、 v·、 w·分别为由传感器测量的弹体坐标系的加速度信息； 矩阵C的表达式为

C=0sinγcosγ0cosγsec－sinγsec1－cosγtansinγtan，

、 ψ、 γ分别为俯仰角、 偏航角、 滚转角； 矩阵B的表达式为

B=B11B12B13

B21B22B23

B31B32B33，

B11=－sincosψu－coscosψcosγv+coscosψsinγw，

B12=－cossinψu+cosψsinγv－sinsinψ·

sinγw+

sinsinψcosγv+cosψcosγw，

B13=sinψcosγv+sin·

cosψsinγv－sinψsinγw+sincosψcosγw， B21=cosu－

sincosγv+sinsinγw，

B22=0，

B23=－cossinγv－cos·

cosγw，

B31=sinsinψu+cossinψcosγv－cossinψsinγw，

B32=－coscosψu－sinψsinγv－sincosψsinγw+

sin·cos

ψcosγv－sinψcosγw，

B33=cosψcosγv－sinsinψsinγv－cosψsinγw－sinsinψcosγw。

1.3 制导与控制方案

采用三维比例导引律为两种制导控制模型提供制导指令， 对于分离设计的制导控制模型和制导控制一体化模型， 制导指令的形式分别如下：

θ·=Nε·cos（η－σ）

σ·=Nη·－Nε·tanθsin（η－σ） （3）

axh=－D－gsinθayh=NVε·cos（η－σ）azh=NVcosθη·－NVε·sinθsin（η－σ） （4）

式中： ε、 η分别为视线倾角和视线偏角； D为气动阻力。

采用滑模控制和反步设计方法设计控制环路， 分离设计的制导控制模型可参考文献［24］， 制导控制一体化模型可参考文献［25］。

2 制导控制一体化模型机理分析

2.1 模型公式的机理分析

制导控制一体化模型的关键数学描述如下［25］：

ωxcωycωzc=（B·C）－1TOHaxhcayhcazhc－TOBu·v·w·（5）

式中：  ωxc、 ωyc、 ωzc分别为三通道角速率指令； axhc、 ayhc、 azhc分別为加速度指令在弹道坐标系的分量。

将B·C的结果整理后可得

B·C=TOB·0w－v－w0uv－u0（6）

将式（6）代入式（5）并整理可得

TTOB TOH axhc ayhc azhc =u·v·w·+ωxc ωyc ωzc ×uvw（7）

式（7）左边为加速度指令在弹体坐标系的分量， 右边第一项为弹体坐标系速度的相对导数， 第二项为牵连加速度。 可以看出， 制导控制一体化模型实际是通过控制弹体坐标系与地面坐标系的牵连加速度来跟踪导引律给出的加速度指令， 由于直接控制三通道角速率而非控制姿态角， 其制导指令的响应过程减少一个积分环节， 使得响应速率更快。

2.2 控制指令分配机理分析

将式（7）进一步整理为误差控制的形式：

ebxebyebz=0w－v－w0uv－u0ωxcωycωzc（8）

式中： ebxebyebz=TBHaxhcayhcazhc－u·v·w·， TBH为弹道坐标系到弹体坐标系的旋转矩阵。

由式（8）可知， 三通道角速率指令是通过非满秩的反对称矩阵进行分配， 矩阵中弹体坐标系速度分量u、 v、 w的大小将影响三通道角速率指令。 在攻角、 侧滑角、 倾侧角均较小的情况下存在uw，uv的数量关系， 因此由误差到三通道角速率指令的分配关系如式（9）所示， 此时飞行器主要采用STT控制模式。

ωxc≈0ωyc≈－ebz/u

ωzc≈eby/u （9）

在攻角或侧滑角较大的情况下， uw， uv的数量关系不再成立， 三通道均产生控制指令， 飞行器采用侧滑转弯和倾斜转弯（Bank To Turn， BTT）混合控制模式。 由于反对称矩阵具有非满秩特征， 矩阵中第一行的范数通常小于其他行， 生成的三通道指令对误差项ebx的控制能力要远弱于对eby、 ebz的控制能力， 因此有关axhc项的信息可以缺省。

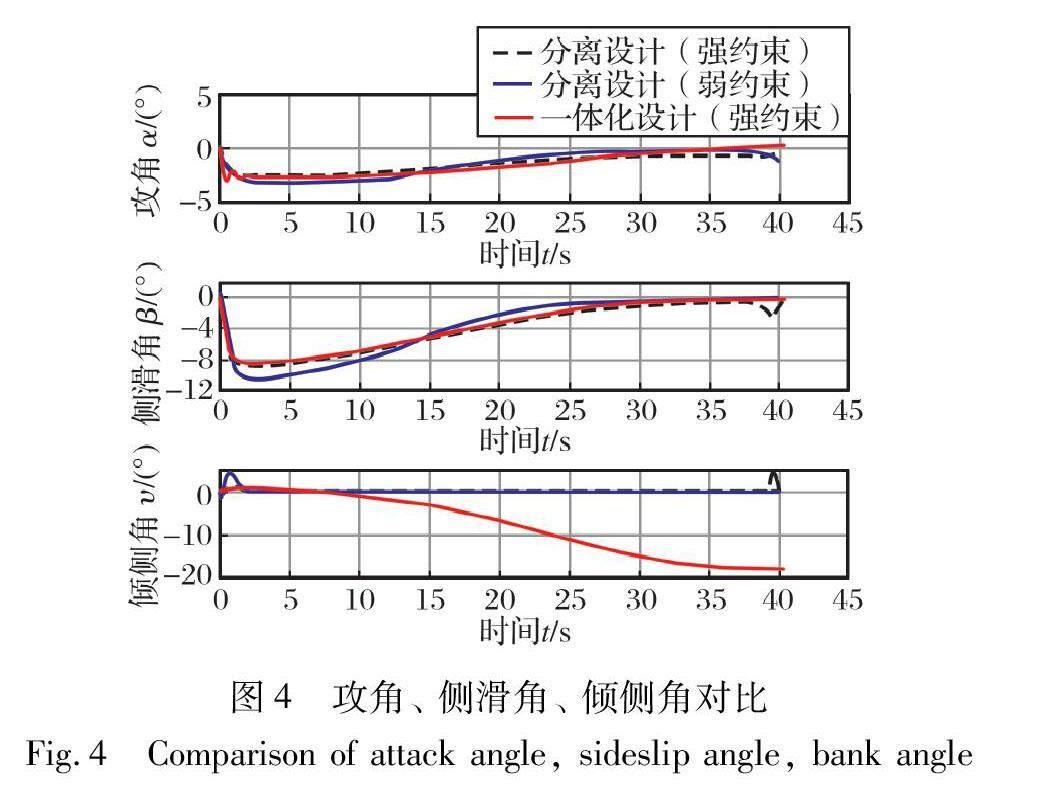
3 弹道特性对比

本节通过高超声速飞行器在约束条件下打击固定目标点的数值仿真， 进一步分析并验证制导控制一体化设计的弹道特性。

3.1 仿真参数设置

高超声速飞行器末段俯冲攻击仿真初值如表1所示。

设置固定目标点坐标为（39， 0， 19） km。 仿真截止条件为高超声速飞行器与目标的相对距离小于10 m或速度小于450 m/s。 高超声速飞行器的舵偏角限幅设置为±30°。

高超声速飞行器的约束条件包含气动过载指令约束和攻角指令约束， 分别设置强、 弱约束条件来对比两种模型对过载的需求， 分别如下：

4 可打击区域的数值仿真与分析

本节将通过确定不同约束条件下高超声速飞行器可打击区域的方法， 将制导控制一体化在单次弹道中需用过载的优势体现为可打击区域的优势， 并在大样本弹道层面分析和验证制导控制一体化放宽需用过载的能力。

确定高超声速飞行器的可打击区域的流程如下： 首先设置供高超声速飞行器打击的地面目标点矩阵， 其次设置合适的仿真初值、 控制器参数、 约束条件， 然后针对目标点矩阵中每一个目标进行六自由度仿真， 最终通过统计高超声速飞行器的终端弹目距离确定高超声速飞行器的可打击区域。

4.1 仿真参数设置

地面目标点矩阵是由若干等距的目标点构成的矩形， 在地面坐标系下表述矩形大小参数为： 纵程范围， 横程范围， 目标点间距离。 由于事先不知道实际的可打击区域范围， 地面目标点矩阵的纵程、 横程范围是在实际的大样本仿真中确定的， 取相邻目标点间的横纵距离均为1 km。 地面目标点矩阵的参数如表2所示

选取纵程跨度Δx、 横程跨度Δz和可打击区域面积Sxz为评价指标以比较可打击区域， 其定义：

Δx=xmax－xmin

Δz=zmax－zmin

Sxz=dxdz （14）

式中： xmax、 xmin分别为目标横坐标为0时， 可打击区域的最大、 最小纵程； zmax、 zmin分别为最大、 最小横程。 高超声速飞行器的初值、 约束条件、 截止条件均与上节相同。 分离设计的制导控制模型和制导控制一体化的控制器参数选择如下：

S1=［α－αc，β－βc，υ－υc］T

S·1c=－5S1－0.01|S1|0.6sat（S1）

S2=［ωx－ωxc， ωy－ωyc， ωz－ωzc］T

S·2c=－5S2－0.01|S2|0.6satS2） ;

S3=［ωx－ωxc， ωy－ωyc， ωz－ωzc］T

S·3c=－5S3－0.01|S3|0.6sat（S3）。

4.2 強约束下的可打击区域对比

强约束条件下分离设计的制导控制模型和制导控制一体化模型的可打击区域如图9～11所示。

如图11所示， 在强约束条件下制导控制一体化模型的可打击区域面积和纵程跨度均优于分离设计的制导控制模型， 但在最大打击横程方面与分离设计的制导控制模型近似。 纵程跨度、 横程跨度和可打击区域面积的指标数值如表3所示。

在强约束条件下， 相比于分离设计的制导控制模型， 制导控制一体化模型的纵程跨度提高了15.8%， 横程跨度持平， 可打击区域面积提高了4.4%， 在强约束下制导控制一体化模型可以提供更大的纵程跨度和可打击区域面积。

4.3 弱约束下的可打击区域对比

弱约束条件下分离设计的制导控制模型和制导控制一体化模型的可打击区域如图12～14所示。

如图14所示， 在弱约束条件下两种模型的优劣势与在强约束条件下相似。 纵程跨度、 横程跨度和可打击区域面积的指标数值如表4所示。

在弱约束条件下， 相比于分离设计的制导控制模型， 制导控制一体化模型的纵程跨度提高了17.4%， 横程跨度持平， 可打击区域面积提高了7.7%， 在弱约束条件下制导控制一体化模型的纵程和可打击区域面积均同样具有优势。

4.4 约束收缩下的可打击区域扩展

如图15所示， 在制导控制控制系统设计当中， 若约束条件从弱约束收缩至强约束， 采用分离设计的制导控制模型的可打击面积将减小， 此时换用制导控制一体化模型可以扩展已损失面积。 结合表3～4可知， 换用制导控制一体化模型可以扩展已损失面积的13.5%。

5 结  论

本文通过对制导控制一体化数学模型公式的分析， 揭示了其通过控制弹体坐标系与地面坐标系的牵连加速度来跟踪制导指令的工作机理。 基于此机理解释了制导控制一体化采用STT/BTT混合控制模式的原因。 基于大样本数值仿真确定飞行器可打击区域的方式， 将制导控制一体化降低需用过载的优势体现为提升可打击区域的能力， 为制导控制一体化的研究提供了一种新思路。

参考文献：

［1］ Ding Y B， Wang X G， Bai Y L， et al. An Improved Continuous Sliding Mode Controller for Flexible Air-Breathing Hypersonic Vehicle［J］. International Journal of Robust and Nonlinear Control， 2020， 30（14）： 5751-5772.

［2］ Ding Y B， Yue X K， Chen G S， et al. Review of Control and Guidance Technology on Hypersonic Vehicle［J］. Chinese Journal of Aeronautics， 2022， 35（7）： 1-18.

［3］ 郭建国， 梁乐成， 周敏， 等. 高速飞行器俯冲段制导控制一体化综述［J］. 航空兵器， 2023， 30（1）： 1-10.

Guo Jianguo， Liang Lecheng， Zhou Min， et al. Overview of Integrated Guidance and Control for Hypersonic Vehicles in Dive Phase［J］. Aero Weaponry， 2023， 30（1）： 1-10.（in Chinese）

［4］ 張登辉. 助推滑翔飞行器多约束制导控制一体化设计方法［D］. 哈尔滨： 哈尔滨工业大学， 2021： 1-8.

Zhang Denghui. Multiple Constraints Integrated Guidance and Control Design Approach for Boost-Glide Vehicle［D］.Harbin： Harbin Institute of Technology， 2021： 1-8.（in Chinese）

［5］ 张宏岩， 王伟， 陈仕伟， 等. 基于全驱系统方法的制导控制一体化设计［J］. 航空学报， 2024， 45（1）： 137-149.

Zhang Hongyan， Wang Wei， Chen Shiwei， et al. Integrated Guidance and Control Design Based on Fully Actuated System Method［J］. Acta Aeronautica et Astronautica Sinica， 2024， 45（1）： 137-149.（in Chinese）

［6］ Ming C， Wang X M， Sun R S. A Novel Non-Singular Terminal Sliding Mode Control-Based Integrated Missile Guidance and Control with Impact Angle Constraint［J］. Aerospace Science and Technology， 2019， 94： 105368.

［7］ Li Z B， Dong Q L， Zhang X Y， et al. Impact Angle-Constrained Integrated Guidance and Control for Supersonic Skid-to-Turn Missiles Using Backstepping with Global Fast Terminal Sliding Mode Control［J］. Aerospace Science and Technology， 2022， 122： 107386.

［8］ Sinha A， Kumar S R， Mukherjee D. Impact Time Constrained Integrated Guidance and Control Design［J］. Aerospace Science and Technology， 2021， 115： 106824.

［9］ Zhou X H， Wang W H， Liu Z H， et al. Impact Angle Constrained Three-Dimensional Integrated Guidance and Control Based on Fractional Integral Terminal Sliding Mode Control［J］. IEEE Access， 2019， 7： 126857-126870.

［10］ Khankalantary S， Sheikholeslam F. Robust Extended State Observer-Based Three Dimensional Integrated Guidance and Control Design for Interceptors with Impact Angle and Input Saturation Constraints［J］. ISA Transactions， 2020， 104： 299-309.

［11］ Chao T， Zhang D H， Wang S Y， et al. Integrated Guidance and Control Design Considering System Uncertainty［J］. Proceedings of the Institution of Mechanical Engineers， Part G： Journal of Aerospace Engineering， 2019， 233（6）： 2278-2290.

［12］ Chang J， Guo Z Y， Cieslak J， et al. Integrated Guidance and Control Design for the Hypersonic Interceptor Based on Adaptive Incremental Backstepping Technique［J］. Aerospace Science and Technology， 2019， 89： 318-332.

［13］ Chong Z Y， Guo J G， Zhao B， et al. Finite-Time Integrated Guidance and Control System for Hypersonic Vehicles［J］. Transactions of the Institute of Measurement and Control， 2021， 43（4）： 842-853.

［14］ Chen K. Full State Constrained Stochastic Adaptive Integrated Guidance and Control for STT Missiles with Non-Affine Aerodynamic Characteristics［J］. Information Sciences， 2020， 529： 42-58.

［15］ Zhang D H， Ma P， Wang S Y， et al. Multi-Constraints Adaptive Finite-Time Integrated Guidance and Control Design［J］. Aerospace Science and Technology， 2020， 107： 106334.

［16］ Hu G J， Guo J G， Zhou J. Integrated Guidance and Control of Interceptors with Impact Angle Constraint Against a High-Speed Maneuvering Target［J］. Proceedings of the Institution of Mechanical Engineers， Part G： Journal of Aerospace Engineering， 2019， 233（14）： 5192-5204.

［17］ Liu W K， Wei Y Y， Duan G R. Barrier Lyapunov Function-Based Integrated Guidance and Control with Input Saturation and State Constraints［J］. Aerospace Science and Technology， 2019， 84： 845-855.

［18］ Liu W K， Wei Y Y， Duan G R. Integrated Guidance and Control with Input Saturation［C］∥ 36th Chinese Control Conference （CCC）， 2017： 6179-6184.

［19］ Tian J Y， Xiong N， Zhang S F， et al. Integrated Guidance and Control for Missile with Narrow Field-of-View Strapdown Seeker［J］. ISA Transactions， 2020， 106： 124-137.

［20］ Zhao B， Xu S Y， Guo J G， et al. Integrated Strapdown Missile Guidance and Control Based on Neural Network Disturbance Observer［J］. Aerospace Science and Technology， 2019， 84： 170-181.

［21］ Bao C Y， Wang P， Tang G J. Integrated Guidance and Control for Hypersonic Morphing Missile Based on Variable Span Auxiliary Control［J］. International Journal of Aerospace Engineering， 2019， 2019： 6413410.

［22］ Bao C Y， Wang P， Tang G J. Integrated Method of Guidance， Control and Morphing for Hypersonic Morphing Vehicle in Glide Phase［J］. Chinese Journal of Aeronautics， 2021， 34（5）： 535-553.

［23］ Liu W K， Wei Y Y， Hou M Z， et al. Integrated Guidance and Control with Partial State Constraints and Actuator Faults［J］. Journal of the Franklin Institute， 2019， 356（9）： 4785-4810.

［24］ Wang J H， Liu L H， Zhao T， et al. Integrated Guidance and Control for Hypersonic Vehicles in Dive Phase with Multiple Constraints［J］. Aerospace Science and Technology， 2016， 53： 103-115.

［25］ Wang J H， Yun C H， Cui Z J， et al. A Novel Partial Integrated Guidance and Control Scheme Based on Three Dimensional Relative Dynamics［C］∥ 40th Chinese Control Conference （CCC）， 2021： 7569-7574.

［26］ Wang J H， Cheng L， Cai Y W， et al. Low-Order Diving Integrated Guidance and Control for Hypersonic Vehicles［J］. Aerospace Science and Technology， 2019， 91： 96-109.

Research on Integrated Guidance and Control Method for

Hypersonic Vehicles for Striking Area

Zhao Liangyu1*， Shi Haoming1， Wang Jianhua2， Cui Lei3

（1. School of Aerospace Engineering， Beijing Institute of Technology， Beijing 100081， China；

2. Department of Aerospace Science and Technology， Space Engineering University， Beijing 101416， China；

3. School of Electrical and Information Engineering， Tianjin University， Tianjin 300072， China）

Abstract： Aiming at the shortcomings of the separation design of guidance and control systems， a method of improving the striking area through integrated design of guidance and control is proposed. Firstly， based on the establishment of an integrated guidance and control model for hypersonic vehicle， the working principle which tracks acceleration commands by controlling the implicated acceleration between the body coordinate system and the ground coordinate system is revealed. Secondly， through numerical simulation of typical trajectories， the ability of integrated guidance and control design to reduce required overload compared to separate design is compared and analyzed. Finally， by determining the separation and integration design of guidance and control in the striking area of hypersonic vehicle， the advantages of integrated guidance and control are reflected from the perspective of large-scale simulation. The results indicate that the integrated guidance and control can relax the demand for available overload and improve the striking area of hypersonic vehicle.

Key words：  integrated guidance and control； large-scale simulations； striking area； hypersonic vehicles； overload constraint