鸭舵转速对双旋弹追随稳定性影响研究
2024-06-03王刚张润桐林海珍席柯
王刚 张润桐 林海珍 席柯


摘 要:发展了适合双旋弹虚拟飞行仿真的高保真计算流体力学和刚体动力学耦合平台, 以此为基础研究了旋转鸭舵对双旋弹弹道追随稳定性的影响。 为了准确刻画双旋弹前后体的差动旋转效应, 将滑移网格算法引入自研非结构混合网格流场数值模拟程序HUND3D。 通过对双旋弹进行定轴转动非定常模拟, 考察了不同鸭舵转速下双旋弹的流动特征与气动特性。 通过耦合求解非定常雷诺平均NS方程和七自由度刚体动力学方程, 实现了双旋弹不同弯度弹道的虚拟飞行仿真, 分析了弹道追随过程的动力学机理, 并结合气动特性分析结果研究了控制鸭舵转速改善弹道追随稳定性的策略。 研究结果表明: 鸭舵旋转所产生的气动干扰, 能够显著影响弹体的侧向力与偏航力矩。 通过控制前体鸭舵转速以产生有利于弹道追随的偏航力矩, 能够在一定程度上改善弹道追随稳定性。
关键词: 双旋弹; 虚拟飞行仿真; 计算流体力学; 滑移网格; 侧向力; 偏航力矩; 追随稳定性
中图分类号: TJ765
文献标识码: A
文章编号: 1673-5048(2024)02-0071-08
DOI: 10.12132/ISSN.1673-5048.2024.0069
0 引 言
随着现代战争对高精度、 低成本制导弹药的需求不断提高, 通过在制式弹药上增加简易制导装置以提升命中精度的弹道修正弹应运而生。 鸭舵式双旋弹作为一种弹道修正弹, 不仅可以利用后体高速旋转产生的陀螺稳定性保持弹轴方向的相对稳定, 防止弹体翻转, 还能通过控制前体鸭舵旋转来提高弹轴跟随速度方向变化的能力, 改善弹丸追随稳定性[1]。 对高速旋转弹丸而言, 提升陀螺稳定性与改善追随稳定性之间通常存在相互博弈的辩证关系: 弹体转速过低可能导致陀螺稳定性不足, 无法保证飞行姿态稳定; 转速过高, 弹丸陀螺稳定性过强, 则可能导致追随稳定性不足, 使得弹丸飞行迎角过大, 影响射程, 甚至出现弹底着地等现象。 因此, 要实现双旋弹高精度、 智能化制导控制的作战效能, 需要在陀螺稳定性和追随稳定性之间寻求平衡。
国内外学者围绕双旋弹的弹道追随稳定性开展了诸多研究。 Murphy[2]采用一阶线性化方法推导了无控弹箭攻角运动方程, 并对旋转弹飞行稳定需要满足的稳定性条件开展了研究。 考虑到前体修正引信对飞行稳定性的影响, 揭涛等[3]基于六自由度外弹道模型建立了采用减旋装置的双旋弹七自由度外弹道模型, 研究了不同射角下双旋弹的弹道追随稳定性, 获得了满足追随稳定性要求的最大射角。 冯单翔[4]基于攻角运动方程理论, 推导了双旋弹动力平衡角公式。 通过与普通旋转稳定弹经验公式对比, 发现双旋弹在弹道顶点处动力平衡角大于普通旋转稳定弹, 双旋弹的追随稳定性较差。
Moss等人[5]曾在研究中指出, 当旋转弹自转速率接近偏航速率时, 会出现灾难性偏航等非线性现象。 对于鸭式布局双旋弹, 常江思等[6]基于小攻角条件推导出的攻角运动方程, 发现前体鸭舵转速与攻角圆运动频率相近时, 会出现共振等不利于飞行稳定的现象。 随着研究的深入, Yin等[7]通过对比URANS(Unsteady Reynolds- Averaged Navier-Stokes)方法与外弹道学理论公式下旋转弹的气动力系数, 发现在较高自旋速率下两种方法获得的气动力系数存在显著差异, 表明理论公式方法在预测气动力方面存在一定的局限性。 基于滑移网格技术与S-A(Spalart-Allmaras)湍流模型, Liu等人[8]研究了后体自转速度、 马赫数以及攻角对双旋弹气动特性的影响, 发现前体翼尖涡能够使得后体气动特性发生周期性变化, 且变化频率等于前体自旋速率。 黄智康等人[9]采用滑移网格技术对超声速状态下双旋火箭弹进行了数值模拟, 分析了鸭舵对弹体侧向力的影响。 研究发现, 鸭舵组件显著影响弹体侧向力, 且加装鸭舵后弹体侧向力系数的非线性随攻角的增加而变强。
综上所述, 目前有关弹道追随稳定性研究大多采用小迎角线性化和准定常假设等简化方法进行研究, 忽略了飞行过程中气动力和力矩的非定常与非线性。 近年来, 数值虚拟飞行仿真[10-11](Numerical Virtual Flight, NVF)已在亚声速旋转弹[12]、 超声速旋转弹[13-14]等高速自转飞行体气动力及飞行历程预测中得到广泛应用, 并取得满意结果。 为研究复杂气动力下双旋弹的追随稳定性, 有必要通过非定常CFD驱动的数值虚拟飞行仿真方法, 精确预测双旋弹所受非定常气动力, 高保真地获得飞行过程中的动力学响应, 进而更准确地进行双旋弹飞行稳定性评估, 研究旋转鸭舵气动干扰对弹道追随稳定性的影响。 为此, 本文建立了适用于双旋弹飞行稳定性研究的高保真数值虚拟飞行仿真平台。 通过对双旋弹进行非定常定轴转动数值模拟以及不同弯度弹道下虚拟飞行仿真, 分析不同前体转速下的气动特性与追随过程动力学机理。 在此基础上, 提出采用鸭舵反转来改善弹道追随稳定性的控制策略, 并通过仿真验证进行效果评估。
1 计算方法
本文通过耦合求解非定常流动控制方程(CFD模块)与七自由度刚体动力学方程(RBD模块), 实现双旋弹数值虚拟飞行仿真。
1.1 非定常流动控制方程
采用自主研发的MPI并行非结构混合网格N-S方程求解程序HUNS3D[15] , 对双旋彈飞行过程中的非定常绕流进行数值模拟, 进而获得非定常气动力。 为了考虑多自由度运动控制体网格相对惯性坐标系的运动, HUNS3D采用任意拉格朗日-欧拉方法(Arbitrary Lagrange-Euler, ALE)描述的积分形式流动控制方程为
tΩQdV+ΩF(Q,Vgrid)·ndS=ΩG(Q)·ndS(1)
式中: Ω代表控制体; Ω代表控制体边界; 守恒变量Q=ρρuρvρwρET, ρ为流体密度, u、 v、 w分别为流体x、 y、 z方向的速度, E为控制体的总内能; Vgrid为网格运动速度; n为控制体表面外法线单位向量; 无粘通量项F(Q,Vgrid)·ndS与粘性通量G(Q)·ndS的具体形式见文献[15]。 网格运动速度Vgrid采用二阶向后差分公式[16]计算获得。
对流动控制方程式(1)中的无粘通量F(Q,Vgrid)·ndS与粘性通量G(Q)·ndS, 使用格心型有限体积法进行离散逼近[17], 可以得到有限体积单元上半离散形式N-S方程:
Qit=-1Ωi(Ri-Rvi)(2)
其中, Ri与Rvi分别为当前单元i的无粘通量项与粘性通量项对残值的贡献。 通过对空间离散后的(2)式采用全隐式双时间格式[18]以完成时间推进, 具体可参阅文献[19]。
1.2 滑移网格技术
通常, 双旋弹由于前后体转速不同存在物面相对运动的情况。 为准确模拟前体鸭舵相对后体旋转对流动的影响效应, 本文在CFD求解程序HUNS3D中发展了滑移网格技术。 考虑到CFD计算过程中需要完成各面单元的通量计算, 而滑移边界面单元只具有其所属网格内侧的流场值, 必须与其他进程进行通信以获得单元外侧流场值。 为实现滑移边界两侧计算数据的通信, 本文采用图1所示的滑移网格算法策略。 以面单元La2为例, 将滑移边界另一侧距离最近的面单元Rb2作为贡献单元, 以贡献单元Rb2及其所有相邻面单元流场值作为插值基, 插值获得La2滑移面外侧的流场值, 从而进行后续通量计算。
为验证所开发的滑移网格算法, 本文进行了近地悬停共轴四旋翼数值模拟。 基本外形参数如下: 旋翼截面翼型为NPL9615, 弦长c=0.18 m, 展长0.625 m, 根梢比为1, 旋翼半径R=1.105 m, 桨距为15°, 无扭矩, 四片旋翼旋转对称。 计算状态如下: 旋翼离地高度h/R=0.52, 翼尖马赫数Ma为0.56, 雷诺数Re为1.44×107, 参考长度取旋翼半径R。 计算网格如图2所示, 图中白色与红色网格分别为滑移边界与旋翼表面网格, 旋翼附面层第一层网格高度Y+为0.8, 法向高度增长率为1.15, 旋翼尾迹区的网格尺度为0.09c。
近地悬停共轴四旋翼滑移边界处流场如图3所示。 图3(b)旋翼翼尖涡在滑移网格边界两侧光滑连续, 以及图3(c)径向截面中流场马赫数等值线的连续分布, 表明了本文所使用的滑移网格数据传递技术能够正确实现滑移边界两侧流场值通信。 图4展示了近地悬停共轴四旋翼数值计算与试验的翼尖涡轨迹空间位置对比图。 图中, 数值计算所得翼尖涡轨迹与试验测量结果[20]基本一致。 此外, 数值计算所得旋翼升力系数0.092 3与试验测量值0.090的差异很小, 表明本文计算结果是准确的。
1.3 七自由度刚体动力学方程
为建立七自由度刚体动力学方程, 本文引入了有关坐标系以描述双旋弹运动与动力学参数。 图5为双旋弹地面坐标系OgXgYgZg、 前体体轴系ObXbYbZb以及弹道坐标系OVXVYVZV的示意图。 地面坐标系原点Og位于双旋弹飞行起始点, Xg轴沿水平线指向初始速度方向, Zg轴铅垂向下, Yg轴由右手定则确定。 前体体轴系原点Ob固联于双旋弹全弹质心, Xb轴沿弹体轴线方向指向前方, Yb轴与Zb轴取为鸭舵面平面的法向量方向。 弹道坐标系原点OV与前体体轴系原点Ob重合, XV轴沿质心平动速度方向指向前方; ZV轴位于铅垂平面内, 垂直XV轴且方向向下; YV轴通过右手法则确定。 通过前体体轴系ObXbYbZb与双旋弹地面坐标系OgXgYgZg的相对方位, 可以给出双旋弹弹轴相对地面的飞行姿态角定义: 俯仰角θ为Xb轴与水平面OgXgYg的夹角, 偏航角ψ为Xb轴在水平面OgXgYg的投影与Xg轴的夹角。 类似地, 可以获得质心速度相对地面的方位θV与ψV的定义。 基于上述坐标系与姿态定义, 可以计算得到外弹道学理论[1]中复攻角: δ=α+iβ=(θ-θV)+i(ψ-ψV)。
本文基于前体体轴系ObXbYbZb将双旋弹前体与后体两组六自由度动力学方程简化为一组七自由度动力学方程。 在前体体轴系下, 质心平动动力学方程矢量形式为
Fb=mdVbdt+ω×Vb(3)
式中: m为双旋弹全弹质量; Fb为质心在前体体轴系下合外力矢量; Vb为质心在前体体轴系下平动速度; ω为前体体轴系相对地面坐标系的旋转角速度。
由于双旋弹前后体间存在约束, 因此将旋转自由度最终简化为俯仰自由度、 偏航自由度以及前后體的两个滚转自由度。 双旋弹绕全弹质心转动的动力学方程具体形式如下:
Mfx=Ifxdωfxdt
Max=Iaxdωaxdt
My=Iydωydt+Ixω-xωz-Izωfxωz
Mz=Izdωzdt+Iyωfxωy-Ixω-xωy
ω-x=Ifxωfx+IaxωaxIx
(4)
式中: M为相对全弹质心的合力矩; I为转动惯量; 下标f与a分别代表双旋弹前体与后体。 对于前体受电机控制维持在恒定转速的情况, 本文将式中前体所受力矩Mfx叠加至后体Max后, 对Mfx进行置零操作。
为求解式(3)与式(4)所组成的常微分方程组, 本文采用了一种改进的Adams预估校正法[16]: 通过已知时间步气动力插值获得校正步所需的下一时间步气动力, 以提高计算效率。
1.4 CFD/RBD耦合流程
图6为数值虚拟飞行仿真平台中CFD/RBD耦合计算流程图。 CFD模块在完成当前时间步计算后输出气动力与力矩系数; RBD模块将CFD输出有量纲化后作为输入参数, 求解获得下一时间步的位移与姿态角变化。 根据RBD求解所得动力学参数, CFD模块对计算网格做出相应的刚体变换, 并计算网格运动速度。 CFD和RBD按照上述流程进行耦合迭代, 直至满足结束条件。
2 计算模型
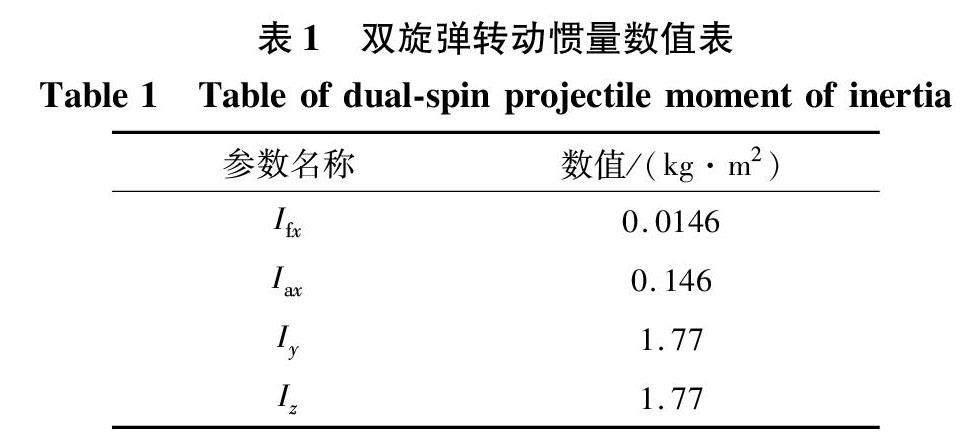
本文所使用的双旋弹计算模型如图7所示。 图中, 双旋弹的四片鸭舵均无安装角, 在飞行过程中通过舵机控制鸭舵偏转实现双旋弹的控制。 模型全弹长为902 mm, 质量m=45.5 kg, 转动惯量具体数值详见表1。
模型计算网格如图8所示。 前体计算网格使用混合网格生成, 附面层第一层网格高度对应的Y+为0.8, 法向高度增长率取1.15; 后体网格为结构网格, 弹身周向布点100个, 前后体计算网格总数为630万。
3 不同前体转速下双旋弹气动特性研究
首先对不同前体转速定轴转动的双旋弹进行非定常绕流模拟, 研究不同前体转速下双旋弹的气动特性, 为后续前体转速对弹道追随稳定性影响研究提供数据支撐。 由于本文主要考察对追随稳定性要求较高的弹道顶点段, 因此选取海拔11 km处大气条件作为来流参数。 具体仿真参数如下: 空气密度ρ=0.358 kg/m3, 声速Va为295.07 m/s, 黏性系数μ为1.421 61×10-5 kg/(m·s), 马赫数Ma=0.72, 雷诺数Re=8.32×105, 参考长度取后体弹径155 mm, 湍流模型采用S-A模型。 双旋弹前体转速ωf分别设为-500π rad/s、 -250π rad/s、 0π rad/s、 250π rad/s、 500π rad/s; 后体转速ωa均为500π rad/s; 攻角α以5°为间隔, 在0°~25°区间内进行选取。
本文所研究的气动力与力矩系数方向如图9所示。 图中所示方向为各气动力(矩)的正方向。 图9(a)为双旋弹侧视图, 升力系数CL与偏航力矩系数CMY均位于攻角平面内, 并分别垂直于来流V与弹轴Xb; 图9(b) 为双旋弹正视图, 侧向力系数CY和俯仰力矩系数CMδ与弹道坐标系YV轴同向, 垂直于攻角平面并指向弹体右侧。
双旋弹在不同前体转速及攻角下的周期平均气动力及力矩系数如图10所示。 由图可见, 双旋弹前体转速对其纵向气动特性影响较小, 但对侧向气动特性影响显著。 随着前体转速增大, 双旋弹侧向力系数CY在负方向上不断增大, 而偏航力矩系数CMY却在对应力矩负方向上逐渐减小, 并且随着攻角的增大, 前体鸭舵转速对双旋弹侧向力及力矩系数的影响增强。 当双旋弹在前体鸭舵转速ωf=500π rad/s、 攻角大于15°且不存在侧滑角的情况下, 其侧向力系数CY与升力系数CL大小相近, 这种显著的侧向力会对双旋弹飞行稳定与落点精度产生不利影响。
为考察前体鸭舵转速对双旋弹气动特性的影响, 以5°攻角为例, 图11给出了前体转速ωf分别为-500π rad/s、 0π rad/s以及500π rad/s时双旋弹的Q准则涡结构示意图。 当ωf=0π rad/s时, 前体鸭舵产生了左右结构较为对称的翼尖涡流; 而当前体鸭舵旋转时, 左右两侧鸭舵由于有效攻角不同, 使得有效攻角较大一侧产生了更强的涡流, 出现翼尖涡结构不对称现象。 图12展示了5°攻角不同前体转速下, 距弹头0.6 m截面处Cp分布与流线图。 受旋转鸭舵不对称翼尖涡影响, 双旋弹后体流动分离区在弹体两侧也呈现明显差异: 当ωf=-500π rad/s时, 弹体左侧的翼尖涡较强, 分离区较ωf=0π rad/s相比向左侧移动, 使得后体左侧Cp偏大, 从而削弱了后体Magnus效应; 当ωf=500π rad/s时, 则会出现与之相反的现象。
针对前体转速增大时, 双旋弹侧向力系数CY在负方向上增大, 偏航力矩系数CMY却在对应力矩负方向上减小这一现象, 图13展示了5°攻角、 不同前体转速下后体两侧截面Cp曲线。 图中, 弹体质心前(Xb>0)的压力系数受主要影响, 且作用力臂更长。 当前体转速增大时, 重心前侧向力减小量大于重心后侧向力减小量, 且重心前气动载荷具有更大力臂, 使得重心前偏航力矩减小量小于后侧部分, 偏航力矩系数CMY在偏航力矩负方向上减小。
4 弹道追随稳定性研究
为研究不同弯度弹道下双旋弹的弹道追随稳定性, 本文选取双旋弹飞行弹道的顶点段, 对双旋弹进行不同弯度弹道的数值虚拟飞行仿真, 弹道轨迹如图14所示。 本文通过改变双旋弹初始弹道倾角θV0以实现弹道弯度的变化。 为减小海拔高度差异所带来的影响, 双旋弹在不同弯度弹道下初始飞行速度V0具有相同的垂直方向分量|V0|sinθV0。 仿真参数方面, 初始大气条件为海拔高度11 km处大气环境; 不同弹道倾角下双旋弹初始飞行速度|V0|分别为318 m/s、 213 m/s、 164 m/s以及134 m/s。 双旋弹初始时刻攻角为0°, 前体初始转速为0π rad/s, 后体转速设为500π rad/s。
图15给出了不同弯度弹道下的复攻角曲线。 图中, 随着弹道弯度增大, 双旋弹复攻角曲线幅值变大, 弹道追随稳定性变差。 为便于阐述双旋弹飞行中的追随过程, 本文将垂直于双旋弹弹轴方向合力矩M⊥分解为水平方向力矩MH与铅垂方向力矩MV, 即M⊥=(MH, MV)。 其中, 水平方向力矩MH垂直于弹轴Xb并位于水平面内, 铅垂方向力矩MV垂直于弹轴Xb并位于铅垂面内。
对于双旋弹的追随过程, 本文以初始弹道倾角θV0=16°弹道为例, 结合飞行过程中姿态角θ、 ψ, 以及力矩MH、 MV等物理量进行分析。 根据双旋弹飞行过程中复攻角实部α与虚部β增减情况, 本文将弹道分为ab-de四个弹道段。 图16展示了双旋弹在θV0=16°弹道下各物理量的变化曲线。 由图可见, 双旋弹弹道倾角θV由于受重力作用不断减小, 弹体俯仰角θ呈现出追随θV的变化趋势。 此外, 在整个飞行过程中, 水平方向力矩MH与α、 铅垂方向力矩β与MV的变化趋势保持一致。
图17展示了双旋弹在四个弹道段内所受气动力矩及角运动情况。 在ab段弹道中, 双旋弹所受水平方向力矩MH随α的增大从0开始增大, 使得高速旋转的弹体向图中左侧开始进动, 出现了β增大的现象。 随着β的增大, 使弹体向下进动以追随弹道倾角θV变化的MV开始增大, 并增大了θ的减小速率。 当双旋弹飞行至b处时, θ变化率超过θV的变化率, α出现极大值。
bc段弹道中, 水平方向力矩MH随着α的减小开始减小至0, 因此双旋弹依然向左进动, β保持增大。 当双旋弹飞行至c处, 双旋弹由于α减小至0而停止向左进动, 出现β极大值。 在cd弹道段, 反向的力矩MH使双旋弹开始向右进动, β与铅垂方向力矩MV开始减小, 进而出现θ的减小速率放缓的情况。 当飞行至d处, 双旋弹俯仰角θ与θV变化率一致, 出现α的极小值。 de弹道段中, 双旋弹由于反向MH作用将继续保持向右进动。 当α增大至0, 双旋弹将再次向左进动。 上述角运动历程循环往复, 便形成了图17中复攻角呈逆时针螺旋并逐渐收敛于β>0、 α≈0复攻角的现象。 当β>0, 双旋弹所受铅垂方向力矩MV方向向下, 使得弹轴向下进動追随弹道倾角θV变化, 有利于弹道追随稳定。
基于上述研究可知, 双旋弹的弹道追随过程是受垂直于弹轴方向合力矩M⊥影响的进动运动。 合力矩M⊥对双旋弹进动运动的影响如图18所示。 图中, 弹轴方向单位向量eδ=(α,β)/α2+β2, M⊥·eδ为合力矩M⊥在弹轴方向投影力矩。 当M⊥·eδ<0, 即合力矩在弹轴方向投影为负时, 弹轴向靠近质心平动速度方向进动, 追随稳定性得到改善。
根据前文对不同前体转速气动特性研究, 前体反转能够显著影响偏航力矩系数CMY, 使其在铅垂方向上投影的力矩增大, 有利于弹道追随稳定性的改善。 因此, 本文对初始弹道倾角θV0=16°、 前体固定转速ωf=-250π rad/s的双旋弹开展了虚拟飞行仿真。 图19(a)给出了双旋弹前体反转前后复攻角曲线对比图。 由图可见, 前体鸭舵反向旋转后, 双旋弹飞行过程中复攻角幅值减小, 弹道追随稳定性得到了一定程度上的改善。 图19(b)中, 前体转速ωf=0π rad/s的双旋弹在弹道顶点段合力矩在弹轴方向投影为正, 存在使弹轴向偏离质心平动速度方向进动的分量; 通过控制前体反向旋转, 能够使合力矩在弹轴方向投影M⊥·eδ的平均值基本为0, 在一定程度上改善了弹道追随稳定性。
图20展示了前体反转前后双旋弹在弹道顶点附近的涡结构。 固定转速ωf=-250π rad/s的双旋弹鸭舵由于有效攻角不同, 在弹体上下两部分产生了不同强度的翼尖涡, 出现了前文所述的鸭舵/弹身气动干扰效应。 相较于ωf=0π rad/s时双旋弹所受的时均偏航力矩MY=0.210 N·m, 前体鸭舵反转后作用于双旋弹上的时均偏航力矩反向, 减小为-0.186 N·m, 使得弹轴更易追随弹道倾角变化, 追随稳定性得到改善。
5 结 论
本文基于所搭建的虚拟飞行仿真平台, 开展了鸭舵转速对双旋弹气动特性与弹道追随稳定性的影响研究, 得到如下结论:
(1) 前体鸭舵转速能够显著影响对双旋弹飞行稳定性不利的侧向气动特性, 且随着攻角的增大, 前体鸭舵转速对双旋弹侧向力及偏航力矩系数的影响增强。
(2) 垂直于弹道方向向下的偏航力矩在双旋弹的弹道追随过程中发挥了关键性作用, 大小和方向合适的偏航力矩可以驱动弹轴向弹道切线方向进动, 进而减小弹体的复攻角, 实现追随稳定。 当弹道弯度增大时, 作用于弹体的偏航力矩可能无法提供足量的进动角度, 双旋弹复攻角幅值变大, 弹道追随稳定性变差。
(3) 采用前体鸭舵相对后体反向旋转的调控策略, 可以在减小侧向力的同时, 增大方向向下的偏航力矩, 产生使弹轴向靠近质心平动速度方向进动的力矩分量, 在一定程度上改善弹道追随稳定性。
以上这些规律在双旋弹的飞行控制中具有潜在的应用价值。
参考文献:
[1] 韩子鹏. 弹箭外弹道学[M]. 北京: 北京理工大学出版社, 2014.
Han Zipeng. Exterior Ballistics of Projectiles and Rockets[M]. Beijing: Beijing Insititute of Technology Press, 2014.(in Chinese)
[2] Murphy C H. Free Flight Motion of Symmetric Missiles[M]. MD, USA: Ballistic Research Laboratories, 1963.
[3] 揭涛, 施坤林. 旋转稳定弹弹道修正引信减旋装置研究[J]. 探测与控制学报, 2007, 29(5): 9-12.
Jie Tao, Shi Kunlin. Study on Despining Device of Course Correction Fuze for Spin-Stabilized Projectile[J]. Journal of Detection & Control, 2007, 29(5): 9-12.(in Chinese)
[4] 冯单翔. 基于精确制导组件的二维弹道修正弹气动与修正研究[D]. 南京: 南京理工大学, 2021.
Feng Danxiang. Research on Aerodynamic and Correction of Two-Dimensional Trajectory Correction Projectile Based on Precision Guidance Kit[D]. Nanjing: Nanjing University of Science and Technology, 2021. (in Chinese)
[5] Moss G M, Leeming D W, Farrar C L. Military ballistics: A Basic Manual[M]. London: Brasseys Publishers Limited, 1995.
[6] 常思江, 王中原, 刘铁铮. 鸭式布局双旋稳定弹强迫运动理论研究[J]. 兵工学报, 2016, 37(5): 829-839.
Chang Sijiang, Wang Zhongyuan, Liu Tiezheng. A Theoretical Study of Forced Motion for Dual-Spin-Stabilized Projectiles with Canards[J]. Acta Armamentarii, 2016, 37(5): 829-839.(in Chinese)
[7] Yin J T, Lei J M, Wu X S, et al. Aerodynamic Characteristics of a Spinning Projectile with Elastic Deformation[J]. Aerospace Science and Technology, 2016, 51: 181-191.
[8] Liu X D, Wu X S, Yin J T. Aerodynamic Characteristics of a Dual-Spin Projectile with Canards[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2019, 233(12): 4541-4553.
[9] 黄智康, 陈少松, 魏恺, 等. 固定鸭舵双旋火箭弹超声速侧向气动特性[J]. 弹道学报, 2021, 33(1): 55-64.
Huang Zhikang, Chen Shaosong, Wei Kai, et al. Lateral Aerodynamics of a Fixed-Canard Dual-Spin Rocket Projectile at Supersonic Speed[J]. Journal of Ballistics, 2021, 33(1): 55-64.(in Chinese)
[10] Zhang L P, Zhao Z L, Ma R, et al. Validation of Numerical Virtual Flight System with Wind-Tunnel Virtual Flight Testing[J]. AIAA Journal, 2020, 58(4): 1566-1579.
[11] Zholtovski S, Stephan A, Holzpfel F. Towards Virtual Flight in Realistic Environments: A Hybrid Coupled Simulation Method[J]. AIAA Journal, 2020, 58(3): 1266-1277.
[12] Sahu J. Virtual Fly-out Simulations of a Spinning Projectile from Subsonic to Supersonic Speeds[C]∥Proceedings of the 29th AIAA Applied Aerodynamics Conference, 2011.
[13] 王勝, 王强, 林博希, 等. 类X-51A飞行器纵向机动数值虚拟飞行仿真[J]. 北京航空航天大学学报, 2021, 47(1): 97-105.
Wang Sheng, Wang Qiang, Lin Boxi, et al. Longitudinal Maneuver Simulation of an X-51A-Like Aircraft Based on Numerical Virtual Flight[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(1): 97-105.(in Chinese)
[14] 王刚, 邢宇, 朱亚楠. 旋转弹气动力建模与飞行轨迹仿真[J]. 航空学报, 2017, 38(1): 120169.
Wang Gang, Xing Yu, Zhu Yanan. Aerodynamic Modeling and Flight Trajectory Simulation of Spinning Projectile[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(1): 120169.(in Chinese)
[15] Wang G, Ye Z Y. Mixed Element Type Unstructured Grid Generation and its Application to Viscous Flow Simulation[C]∥24th International Congress of the Aeronautical Sciences, 2004: 1-8.
[16] Wang G, Zeng Z, Suo Q. Trajectory Simulation of a Spinning Projectile Based on Variable Step Size CFD/RBD Method[C]∥Proceedings of the AIAA Atmospheric Flight Mechanics Conference, 2015.
[17] Venkatakrishnan V. Perspective on Unstructured Grid Flow Solvers[J]. AIAA Journal, 1996, 34(3): 533-547.
[18] Jameson A. Time Dependent Calculations Using Multigrid, with Applications to Unsteady Flows Past Airfoils and Wings[C]∥Proceedings of the 10th Computational Fluid Dynamics Conference, 1991.
[19] Wang G, Liu Y, Mian H H, et al. A NUFFT Technique for Flow Fluctuation Analysis Based on the Unsteady Flow Simulation with Variable Physical Time Stepping Scheme[C]∥Proceedings of the 32nd AIAA Applied Aerodynamics Conference, 2014.
[20] Light J S. Tip Vortex Geometry of a Hovering Helicopter Rotor in Ground Effect[J]. Journal of the American Helicopter Society, 1993, 38(2): 34-42.
Study on Influence of Canard Rotation Speed on Following
Stability of Dual-Spin Projectile
Wang Gang1, 3*, Zhang Runtong1, 3, Lin Haizhen1, 3, Xi Ke2
(1. School of Aeronautics, Northwestern Polytechnical University, Xian 710072, China;
2. Research Institute of Navigation and Control Technology, Beijing 100089, China;
3. National Key Laboratory of Aircraft Configuration Design, Xian 710072, China)
Abstract: A high-fidelity computational fluid dynamics and rigid-body dynamics coupling platform suitable for virtual flight simulation of dual-spin projectile is developed. Based on this platform, the influence of rotating canards on the trajectory following stability of the dual-spin projectile is studied. To accurately characterize the differential rotation effect of the dual-spin projectiles fore and aft bodies, a slidingmesh algorithm is introduced into the in-house unstructured mixed grid flow field numerical simulation program HUND3D. By conducting axisymmetric rotational unsteady simulations of the dual-spin projectile and investigating the flow characteristics and aerodynamic properties under different canard rotation speeds, the dynamics mechanism of the trajectory following process is analyzed. Through the coupled solution of unsteady Reynolds-averaged Navier-Stokes equations and seven-degree-of-freedom rigid-body dynamics equations, virtual flight simulations of the dual-spin projectile with different curvature trajectories are realized. The dynamic mechanism of the trajectory tracking process is analyzed, and strategies for improving trajectory following stability by controlling the canard rotation speed based on the analysis of aerodynamic characteristics are studied. The research results indicate that the aerodynamic disturbances generated by canard rotation can significantly affect the lateral force and yawing moment of the projectile. By controlling the rotation speed of the fore canards to produce a yawing moment favorable for trajectory tracking, the trajectory following stability can be improved to a certain extent.
Key words: dual-spin projectile; virtual flight simulation; computational fluid dynamics; sliding mesh; lateral force; yawing moment; following stability
