大件运输车组通过混凝土简支空心板梁桥检测方法

郭斌

摘要 文章采用常见的小载荷车组，在预应力混凝土简支空心板梁桥面上进行布载，对桥梁上部结构变形进行实时监测，采用理论分析方法对横向分布系数进行验证。建立MIDAS/Civil有限元仿真模型，对大件运输车组通过桥梁时的荷载状态进行模拟加载，分别对桥梁上部结构和下部结构抗弯承载力和抗剪承载力进行验算。结果表明，实测横向分布系数与理论计算结果变化趋势一致，实桥有限元模型能对桥梁承载力进行可靠度评估，明确大件运输车组是否能够安全通行。

关键词 大件运输车组；混凝土；空心板梁桥；检测方法

中图分类号 U223文献标识码 A文章编号 2096-8949（2024）06-0055-04

0 引言

根据交通运输部在2020年年底统计的数据，我国公路总里程已达到5 200 000 km，形成以高速公路为骨架，普通干线为脉络，农村公路为基础的全国公路网，桥梁总数达到91.28万座，中小跨径的桥梁占桥梁总数86%以上[1]。由于混凝土材料具有抗压力不承抗拉的特点，钢筋混凝土桥梁在外部荷载、腐蚀环境、材料老化等条件下，存在结构强度下降、表面出现裂缝、动力力学特性降低等安全隐患，中小跨径预应力混凝土桥梁的安全威胁更加显著[2-3]。Maas等[4-5]利用研发的一种冲击装置对大跨径桥梁进行了静载试验和冲击试验，发现桥梁结构的预测挠度与计算挠度基本吻合；亓兴军等[6]利用模态挠度代替静载挠度，用来评估简支空心板桥的实际承载力，得到了广泛的应用。

近年来，随着我国基建事业的快速发展，利用公路桥梁运输特大、特重型的工业设备日趋频繁，公路桥梁受到的荷载显著增加。由于原有公路桥梁承载能力下降，以及设计荷载等级的限制，无法满足大件运输车辆的安全通行[7]。为了确保公路桥梁承载力能够满足要求，在大件运输车组通行过程中需要对桥梁上部结构进行监测，并采用MIDAS/Civil有限元软件对其承载力进行数值模拟，研究大件运输车组通行中桥梁性能的变化。

1 工程背景与桥梁静载试验

1.1 工程背景

公司某桥式运输项目车组需要通过桥结构形式为预应力混凝土的简支梁桥，跨径组合为17.8 m×4+18.6 m+

17.8 m，主墩采用空心混凝土墩内填毛石及砂砾石，边跨采用重力式桥台和桩柱式桥墩，空心板梁梁高均为0.85 m，梁底宽均为1 m，边梁翼缘宽度为0.25 m。主要技术标准：桥梁全长112.45 m，桥面铺装为8 cm沥青混凝土面层，13 cm厚钢筋混凝土垫层。设计荷载：汽车-超20 t、掛车-120 t。桥面宽度：28 m=0.5 m（防撞护栏）+12.5 m（车行道）+2 m（中央分隔带）+12.5 m（车行道）+0.5 m（防撞护栏）。如图1所示，为预应力混凝土简支梁桥横断面形式布置图，梁号从左到右依次为1#、2#、3#……13#。为确保大件运输车组能够在桥梁上正常通行，分别对其进行上部结构变形监测、桥梁静荷载试验、有限元数值模拟，以此判断该桥梁是否处于安全状态，为桥梁安全正常运营提供技术保障。

1.2 桥梁状态监测

1.2.1 试验荷载

根据《公路桥梁荷载试验规程》（JTG/T J21-01—2015）[8]为依据，桥梁的静力试验按荷载效率ηb来确定试验的最大荷载，则静载效率ηb的计算公式如式（1）所示：

式中，Ss——静载试验下，某一加载试验项目对应的加载控制截面内力或位移的最大计算效应值；S——控制荷载产生的同一加载控制截面内力或位移的最不利效应计算值；μ——按规范取用的冲击数值。

1.2.2 运输车荷载横向分布系数测试

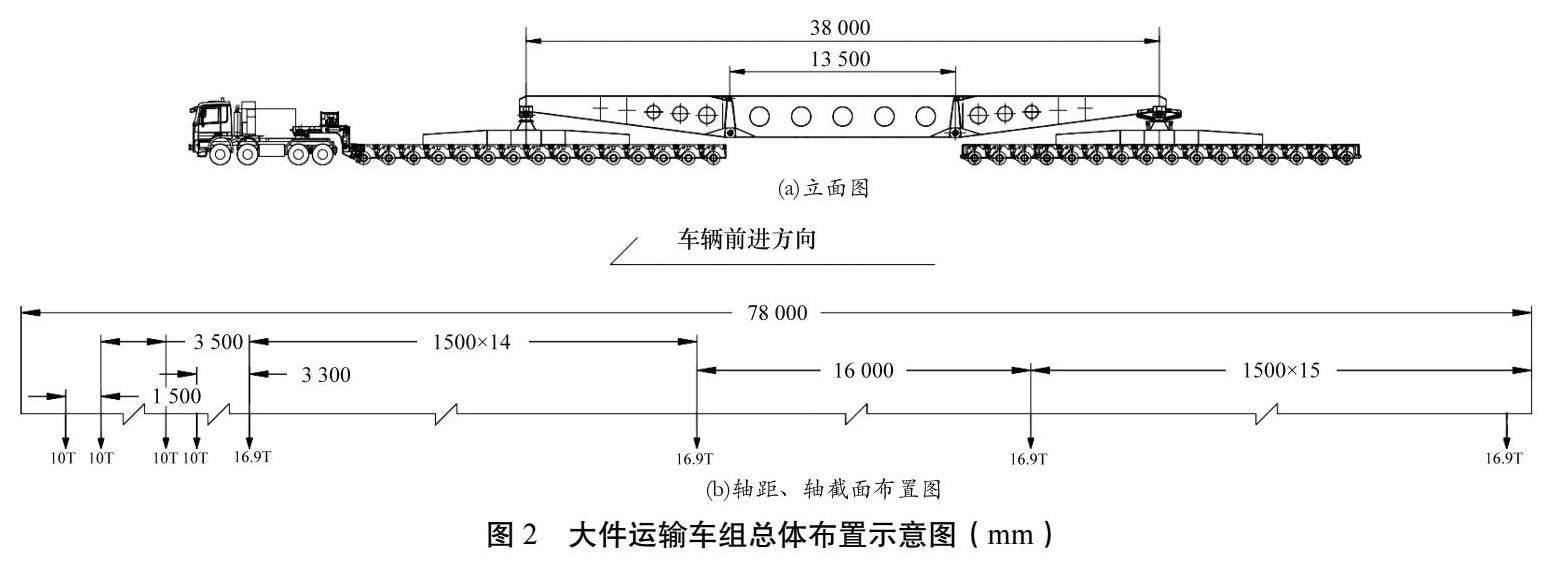
在大件运输车组通过桥梁前，需要对其进行检测，检测后整个桥梁在设计荷载下技术状态评定等级为2类。该文大件运输车组选用的主车自重15 t，挂车自重175 t，货物总重375 t，平均荷载16.9 t，大型设备在整个运行过程中不可拆卸。大件运输车组总体布置如图2所示。

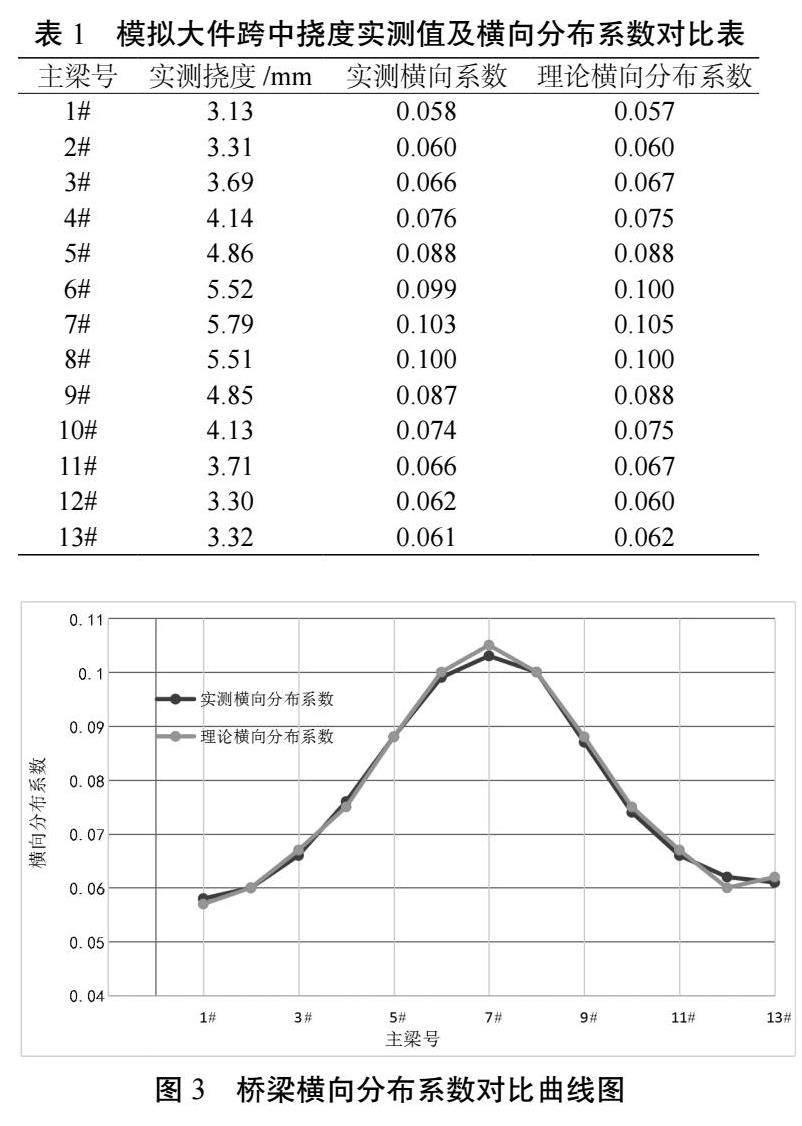
如表1所示，为大件车运输车组挠度实测值及横向分布系数。如图3所示，为桥梁横向分布系数对比。从表1和图3可以看出，大件运输车组测试的桥梁上部结构横向分布系数与理论横向分布系数基本相吻合，其中实测横向分布值7#梁最大，最大值为0.103，理论横向分布值7#梁最大，最大值为0.105，实测值较理论值略小。实测横向分布系数曲线与理论值变化趋势一致，且实测横向分布曲线较为平滑，无明显突变，表明空心板梁间横向连接良好。

1.2.3 静载试验

该试验加载方式采用5辆42 t载重车进行加载，加载分2级进行（1级加载1～3号车，2级加载4～5号车），车辆布置方式如图4所示。单梁试验荷载为494.54 kN，由式（1）计算得到荷载效率为1.00。应变实测值与校验系数如表2所示。从表2可知，5#梁校验系数的主要测点中最大的，实测应变值/理论应变值为0.50，小于规范限制值0.70。因此，在工况满载作用下，桥梁的校验系数满足规范要求，具有一定的安全储备。其中，8#梁二级加载挠度值最大，实测挠度值为?5.29 mm，实测挠度值与理论挠度值之比为0.49，远小于规范值0.7，故在工况满载作用下，桥梁的校验系数满足规范要求，也具有一定安全储备。

2 大件运输车组荷载验算

该文验算采用荷载效应对比法对该次大件运输车组过桥荷载进行验算，计算桥梁取汽车-超20级（计算荷载）及挂车-120（验算荷载），公式为：

S=1.2SG+1.4SQ1 （2）

S=1.2SG+1.1SQ2 （3）

式中，SG——永久荷载中结构重力产生的效应；SQ1——基本可变荷载中汽车荷载产生的效应；SQ2——基本可变荷载中平板挂车或履带车产生的效应。其余桥梁参照《城市桥梁设计荷载标准》（CJJ 77—98）中规定[9]，使用城-A级汽车荷载进行验算。

2.1 桥梁上部结构承载能力极限状态

对于空心板梁，跨中截面采用铰接梁法来计算其荷载横向分布系数，支点处采用杠杆原理计算在大件运输车组荷载作用下的横向分布系数。由于大件运输车组应行驶在桥梁的中间车道上，避免走两侧的车道而造成没有必要的结构受力增大，故采用MIDAS/Civil 2021建立桥梁上部结构的单梁模型，如图5所示，由该软件计算得出7#梁横向分布系数最大。该程序计算得到空心板梁在恒载及大件运输车组荷载作用下的跨中最大正弯矩为625.55 kN·m，支点最大剪力为142.98 kN。

2.1.1 抗弯承载力

采用单梁法将计算荷载与验算荷载加载至单梁结构上，通过横向分布系数计算最不利荷载分布在主梁上进行荷载效应对比验算。在特殊车辆荷载作用下产生的内力乘以横向分布系数，再加上恒载内力（自重及二期恒载），计算得到7#梁的组合内力值，7#梁抗弯验算结果如表3所示。从表3可知，汽车-超20级计算荷载为1 289.68 kN，挂车-120计算荷载为1 398.20 kN，正截面抗弯承载力为1 479.59 kN，三者均满足规范[8]要求。

2.1.2 抗剪承载力

根据该桥现状，利用MIDAS/Civil大型有限元结构分析软件，结合单梁法对主梁最不利布载下进行荷载效应对比验算，计算支点截面最大组合剪力为293.84 kN，其汽车-超20级支座处最大剪力为319.73 kN，挂车-120支座处最大剪力为340.71 kN，斜截面抗剪承载力支座处最大剪力为808.16 kN。其计算荷载和验算荷载均能满足规范[8]要求，结构安全。

2.2 桥梁下部结构承载能力极限状态

对桥梁进行有限元建模，将最不例外荷载作为外力施加在盖梁上，对其进行结构验算，模型及盖梁布置图如图6所示。当核算对象为盖梁抗弯（正弯矩）时，大件运输车组荷载为284.31 kN·m，正截面抗弯3 660.2 kN·m；当检测对象为盖梁抗剪时，大件运输车组荷载为628.64 kN·m，斜截面抗剪承载力为3 660.20 kN·m；当检测对象为墩柱抗压时，大件运输车组荷载为?1 859.04 kN·m，墩柱抗压承载能力为?13 006.19 kN·m。因此，在给定的大件运输车组荷载作用下，下部结构的承载力极限状态验算能满足规范要求，结构安全。

3 结论

（1）在大件运输车组通过简支桥梁过程中，监测得出该桥上部结构的横向分析系数与理论分析系数基本吻合，两种方法结果一致，均得出7#梁横向分布值最大，实测值略小于理论值。

（2）采用常见小吨位车辆在桥梁上布载，结合荷载效应对比法，对桥梁上部和下部结构的抗弯承载力、抗剪承载力进行了验算。结果表明：桥梁结构承载力能够满足大件运输车辆沿桥梁安全通行的需求。

（3）构建了MIDAS/Civil有限元仿真模型，对大件运输车辆通过桥梁实际状态进行了模拟加载，计算结果与实测数据相吻合，表明该模型能够模拟桥梁的实际工作状态，为大件运输车组能否通过桥梁提供判断依据。

参考文献

[1]2020年交通运输行业发展统计公报[J]. 交通财会， 2021（6）： 92-97.

[2]于贵， 张宇， 柯佳闻. 铁路简支T梁横向预应力加固方法[J]. 铁道建筑， 2019（6）： 20-24.

[3]亓兴军， 孙绪法， 周广利， 等. 损伤状态下预应力混凝土简支梁的模态挠度和模态刚度试验研究[J]. 2023（21）： 227-236+262.

[4]Maas S. ， Nguyen V. H. ， Kebig T. ， et al. Comparison of different excitation and data sampling-methods in structural health monitoring[J]. Civil Engineering Design， 2019（1）： 10-16.

[5]Xue M. S. ， Yi T. H. ， Qu， C. X. ， et al. Bridge flexibility identification through a reference-free substruring integration method driven by mode fitting[J]. Journal of Engineering Mechanics， 2022（3）： 04021164.

[6]亓興军， 赵越， 赵奇. 基于模态挠度的斜交桥静载试验数值方法[J]. 建筑科学与工程学报， 2020（3）： 55-62.

[7]刘尧. 公路桥梁在大件运输中的若干问题研究[D]. 杭州：浙江大学， 2006．

[8]公路桥梁荷载试验规程： JTG/T J21-01—2015[S]. 北京：人民交通出版社股份有限公司， 2016.

[9]城市桥梁设计荷载标准： CJJ 77—98[S]. 北京：中国建筑工业出版社， 1998.