塔式起重机顶升腰环尺寸优化设计*

邹 进 马思群 詹 健 陶 然 李 健

1 大连交通大学 大连 116028 2 大连盖斯特工程机械技术有限公司 大连 116022

0 引言

塔式起重机是一种臂架位于基本垂直的塔身顶部、由动力驱动的回转臂架型起重机，广泛应用于建筑与工业以及石油、冶金、各种发电站和桥梁等行业大型建设工程的施工和吊装，对降低工程造价和缩短工期有着重要的作用[1]。塔式起重机的工作机构中主要包括起升机构、变幅机构、回转机构、运行机构和顶升机构等。其中，顶升机构更多的是采用液压顶升方式，通过电动机驱动液压泵将电能转化为液压能，驱动液压缸下支座以上部分与塔身标准节脱开，从而实现塔身的升高与降低动作，具有构造简单、工作平稳、操纵方便和爬升速度快等优点[2]。

随着建筑科技水平机械制造水平的提高，塔式起重机的需求越来越趋于大型化，这种大型化在提高工人工作效率的同时安全问题也越来越凸显出来；而在众多塔式起重机发生的安全事故中，因顶升装置导致的事故往往会造成严重后果，甚至危及操作者生命[3]。当顶升到一定高度时，需要安装顶升腰环，以便保证塔身的稳定，腰环配置对抱杆的安全使用起着关键作用[4]。然而，近年来对顶升腰环进行强度分析和优化的研究较少。

鉴于此，本文以塔式起重机顶升腰环为研究对象，首先进行有限元静强度分析，其次通过灵敏度分析确定优化前后的最大应力和质量进行对比，在保证设计可靠性和安全性的同时实现轻量化，为塔式起重机顶升腰环尺寸优化设计提供参考。

1 起重机顶升腰环有限元分析

1.1 顶升腰环有限元模型的建立

塔式起重机顶升腰环的总质量为8 957 kg，主要由举升架、滑轮、横板等部分组成，各部分板厚均在100 mm以下，有限元模型采用Shell 181单元，单元尺寸设为15 mm，运用Hypermesh建立其有限元模型，离散后的总结点数为26 528，总单元数为27 158。建立的顶升腰环有限元模型如图1所示。

图1 顶升腰环有限元模型

顶升腰环结构选用低合金高强度结构钢Q390，其主要材料参数有：密度为7.85×10-9t/mm3，弹性模量为2.1×105MPa，泊松比为0.3，屈服强度为390 MPa。

1.2 建立加载工况

依据标准GB/T 3811—2008《起重机设计规范》，各工况下顶升腰环应力必须小于或等于所选材料的许用应力，其表达式为

式中：σ为顶升腰环各部分计算最大VonMises应力值；[σ]为许用应力值，[σ]＝177.3 MPa；σs为材料的屈服强度；n为安全系数（本文中静载和风载工况下安全系数均取2.2）。

在设计计算中，常用第四强度理论校核结构静强度，其含义为：在任一应力状态下，材料不发生强度破坏的条件，即

式中：σ1、σ2、σ3为第1、第2、第3主应力，[σ]为材料的许用应力值[5]。

为了便于加载计算，将液压缸固定板的轴套中心处采用CE单元连接，并约束其6个方向自由度。将自重和风压均加在横梁上，模拟工作状态下顶升腰环受到的总载荷.在背风面的2个横梁上施加载荷F1，在迎风面的2个横梁上施加载荷F2，选取工作状态下6级风，风向由y轴负向沿y轴正向，受风向影响F1大于F2的值。建立8个计算载荷工况，具体数据如表1所示。

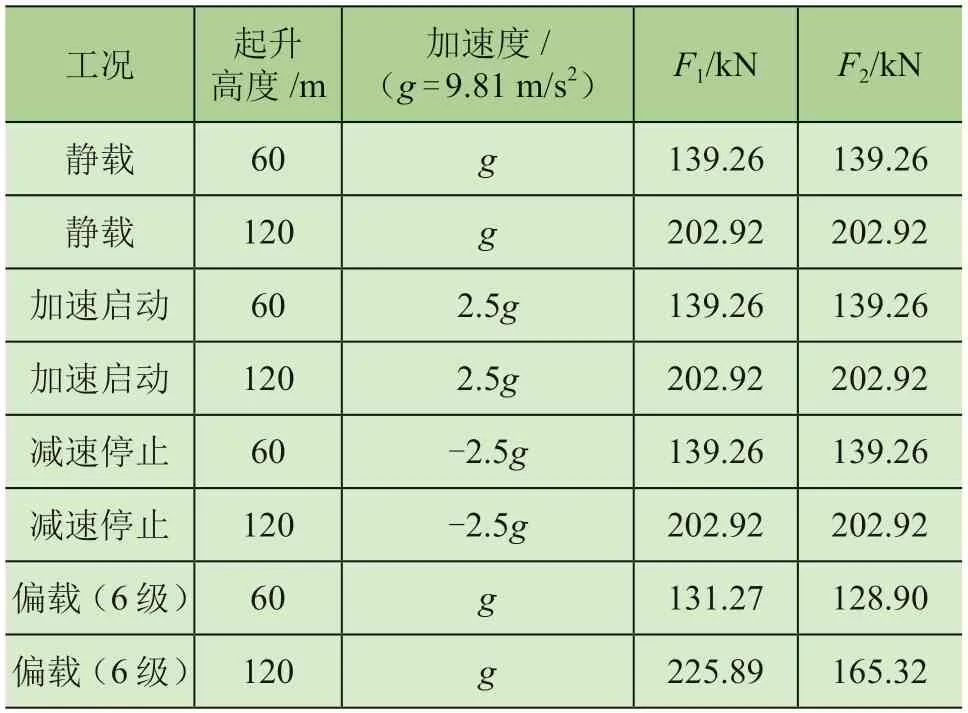
表1 顶升腰环计算载荷工况汇总

1.3 有限元分析结果

利用有限元分析软件Ansys对顶升腰环有限元模型进行静力学计算，由于第7、第8工况为风载工况，且第8工况为危险工况，在此仅给出风载第7、第8工况下的最大VonMises应力云图，如图2和图3所示。

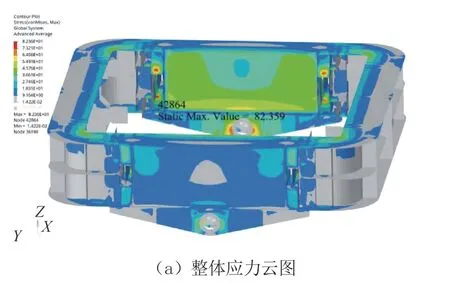
图2 顶升腰环优化前工况7的VonMises应力云图

图3 顶升腰环优化前工况8的VonMises应力云图

计算结果表明，在8种载荷工况下最大VonMises应力发生在第8工况，最大应力值为146.168 MPa，最大应力发生位置在液压缸固定板和轴套的交界位置，小于材料的许用应力值177.3 MPa。经初步计算，顶升腰环各工况均满足强度设计要求，且最大应力值均小于许用应力值，说明该设计合理。因此，针对顶升腰环的最大VonMises应力和质量还有优化空间，可进一步进行尺寸优化。

在尺寸优化前，首先应进行灵敏度分析，灵敏度分析可得出对顶升腰环强度影响明显的设计参数，通过相应参数的分析筛选，对顶升腰环进行合理的尺寸优化，在提升其力学性能基础上进行轻量化设计。

2 顶升腰环灵敏度分析

2.1 灵敏度分析原理

灵敏度分析方法反映了结构参数与设计变量对目标函数影响的变化情况，通过此方法可分析出各关注变量对目标函数的贡献程度和敏感性参数值。灵敏度分析方法通过寻求最优搜索路径构建准则方程，设立对应迭代公式[6]。目前，常采用改变不同板件厚度求出目标函数对厚度的导函数，并进行排序，从而得出导函数值下的最大设计变量，该变量即为重点关注的变量。

灵敏度S用以评估顶升腰环结构设计变量的改变对其结构响应的影响程度，进而获得符合要求的灵敏度系数和最佳设计参数[7]。即

式中：Tj为第j个结构的性能参数，xi为第i个部件厚度。

2.2 顶升腰环灵敏度分析

在灵敏度分析理论中，若灵敏度值为正时，则表明该板件对某阶模态频率灵敏度越高。提高板件厚度对增加对该板件强度有着更突出的作用，若灵敏度为负值时，则正好与之相反[8]。

将顶升腰环所有板厚（共10组）作为设计变量，利用Workbench软件中的响应面分析模块，采用拉丁超立方取样方法抽取40组数据进行计算，最后将结果导入Origin中得到灵敏度结果图，结果如表2和图4所示。表2给出设计变量名称和各板厚度，图4给出了各板厚应力灵敏度的计算结果。

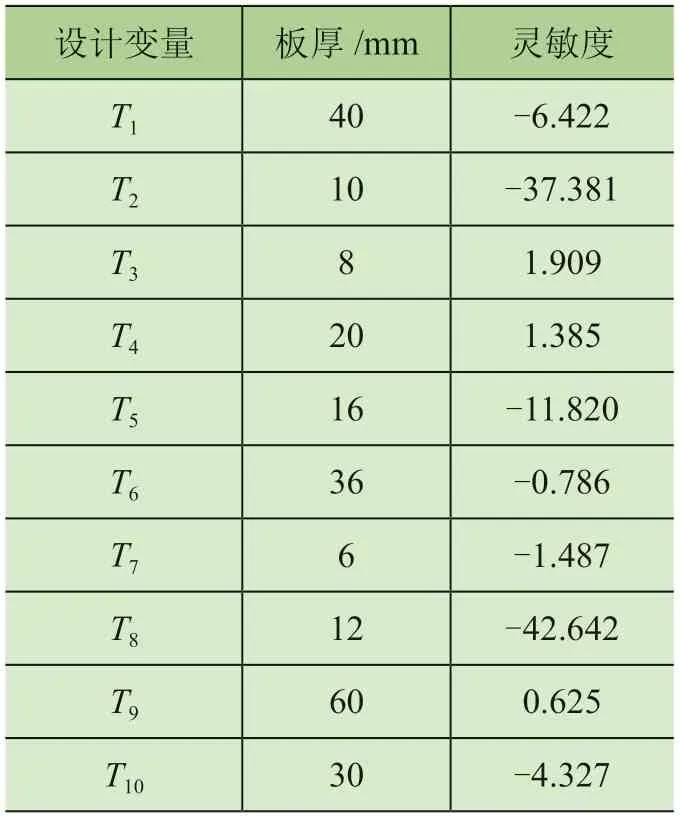
表2 设计变量所对应板厚

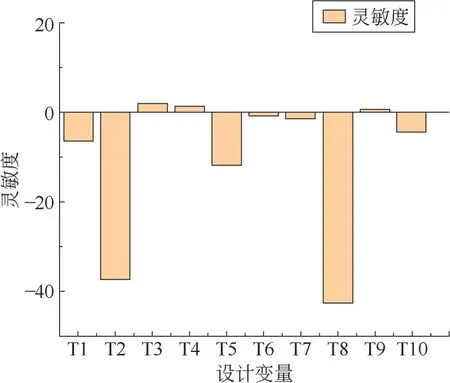
图4 各板厚灵敏度

计算结果表明，液压缸固定板中轴孔处板厚为36 mm和滚轮调整座处板厚为60 mm的灵敏度系数绝对值均小于1，这2板对顶升腰环的强度性能和轻量化程度的提高影响很小。因此，将除这2板外的其他各板的板厚作为设计变量，通过优化软件对其进行尺寸优化。

3 Optistruct软件的优化设计方法

Optistruct是一款功能强大的结构优化软件，支持非常全面的优化类型，包括概念设计阶段的拓扑优化、形貌优化和自由尺寸优化，以及详细设计阶段的尺寸优化、形状优化和自由形状优化。优化设计包含设计变量、目标函数和约束条件三要素[9]。其中，设计变量是发生改变从而提高性能的一组参数；目标函数要求最优的设计性能，是关于设计变量的函数；约束条件是对设计变量和其他性能的要求[10，11]。除此之外，优化的数学模型可表示为

式中：X＝（x1，x2，…，xn）为设计变量，f（X）为设计目标，gj（X）和hk（X）为需要进行约束的设计响应[12]。

本文中将对顶升腰环进行尺寸优化，尺寸优化是最常见的优化技术，又称为参数优化技术。对于不同的设计阶段，尺寸优化可分为2种类型：用于详细设计的尺寸优化技术和用于概念设计的自由尺寸优化。在详细设计阶段的实际工程应用中，经常会采用离散变量进行优化[13]。

4 顶升腰环尺寸优化设计

4.1 顶升腰环优化数学模型

顶升腰环有限元模型由壳单元构成，以灵敏度分析筛选后的顶升腰环各部分板厚为设计变量，最危险工况的最大VonMises应力为约束条件，顶升腰环的质量最小为优化目标，利用Optistrust软件对顶升腰环8个影响较大的各部位板厚进行尺寸优化。顶升腰环优化的数学模型为

式中：x为设计变量，M为顶升腰环总质量，σmax为最大VonMises应力。

当顶升腰环优化时，各设计变量初始值及其变化范围（原始值基础上下浮动20%）如表3所示。

表3 设计变量的初始值及其上下限 mm

4.2 顶升腰环尺寸优化结果分析

将顶升腰环尺寸优化模型提交Optistrust计算，优化目标经历3次迭代运算后结果收敛，查看优化后得到的Out结果文件，优化后顶升腰环各部分板厚如表4所示。

表4 设计变量优化后结果 mm

4.3 优化前后应力质量对比分析

将优化后导出的cdb文件和计算后得到的rst文件导入Hyperview中查看应力云图，优化后第7、第8工况的最大VonMises应力云图如图5和图6所示。

图5 顶升腰环优化后工况7的VonMises应力云图

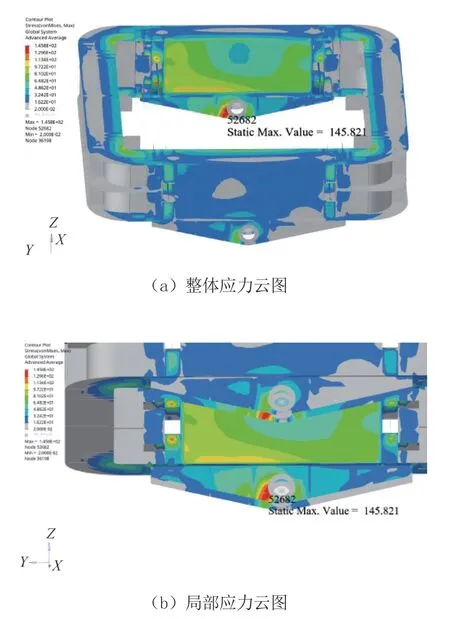
图6 顶升腰环优化后工况8的VonMises应力云图

优化前后各工况最大VonMises应力值及最大应力发生位置如表5所示。

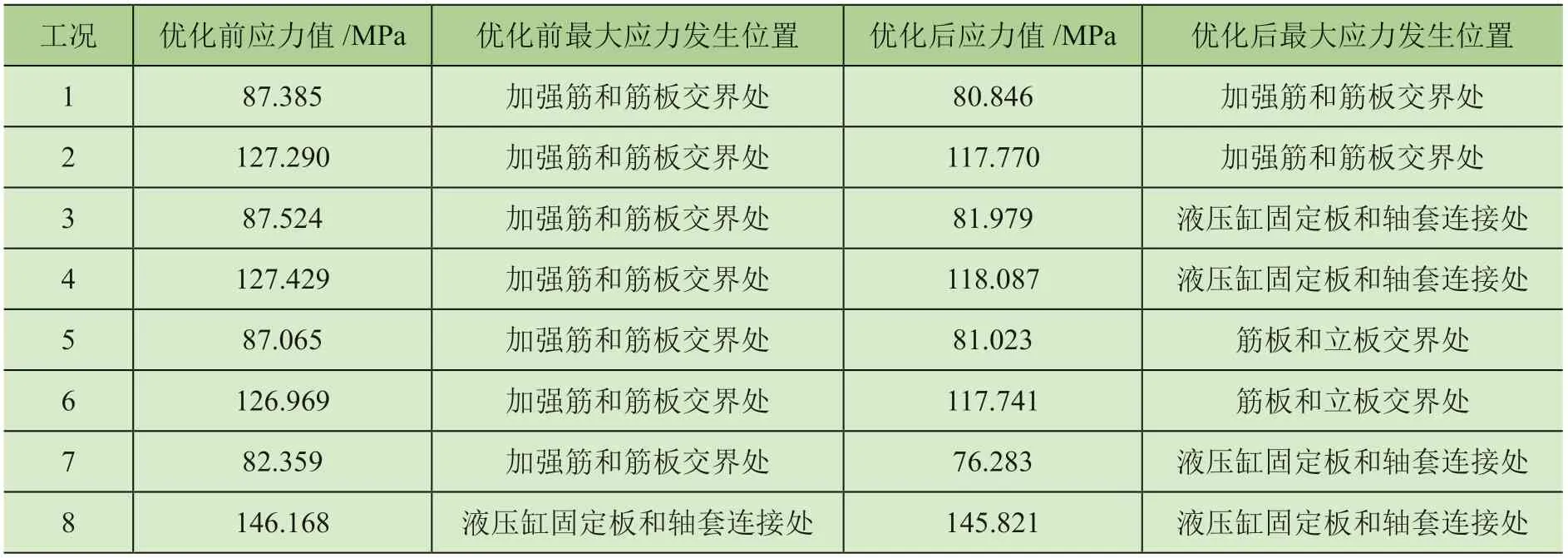
表5 优化前后最大应力值和最大应力发生位置

由表4、表5可知，优化后设计变量数值与优化前相比整体有所下降，8种工况的最大VonMises应力均有降低，且均远小于材料许用强度。顶升腰环各部位应力分布更加均匀，优化前顶升腰环总质量为8 957 kg，优化后的总质量达到8 042 kg，质量降低10.22%，达到了轻量化的目的。

5 结论

以塔式起重机顶升腰环为研究对象，通过有限元建模分析对其进行静强度计算，针对其结构性能和轻量化提出了尺寸优化设计方法，并通过灵敏度分析筛选出对应力影响较大的板，以此进行尺寸优化计算，为顶升腰环结构设计提供了可行性方案。

优化结果表明：在顶升腰环静强度分析的基础上，对其进行尺寸优化设计，优化后8个工况的最大VonMises应力均有所降低，结构总质量达到8 042 kg，比原有结构降低10.22%。由此可知，通过尺寸优化后顶升腰环结构应力分布更加合理，有效地实现了结构轻量化，说明尺寸优化设计是轻量化设计中的一种有效的优化设计方法，此研究内容可为其他相关产品轻量化及经济性设计提供合理参考。