基于案例引导的可靠性理论教学模式探析

吴兴征 王瑞凯 宋鹏彦

doi：10.11835/j.issn.1005-2909.2024.03.018

欢迎按以下格式引用：吴兴征，王瑞凯，宋鹏彦.基于案例引导的可靠性理论教学模式探析［J］.高等建筑教育，2024，33（3）：144-153.

修回日期：2022-04-15

基金项目：河北省省级研究生专业学位教学案例库项目“工程结构可靠度案例教学”（KCJSZ2022006）；河北省自然科学基金面上项目“考虑参数不确定性的基桩几何可靠性算法与试验研究”（E2019201296）

作者简介：吴兴征（1971—），男，河北大学建筑工程学院副教授，博士，主要从事岩土、防洪与海岸工程中不确定性模型研究，（E-mail） xingzhengwu@163.com；（通信作者）王瑞凯（1993—），男，衡水学院电子信息工程学院助教，硕士，主要从事可靠性理论研究，（E-mail）ruikaiw@163.com。

摘要：常规可靠性理论教学存在重视公式推导而轻视案例分析的现状，课程教学效果不佳。文章探索用案例教学法讲授该课程知识，着重强调案例教学理念与编程实践促学的重要性。结合4个典型工程案例，如悬臂梁、海堤、基桩、板桩墙等构筑物，说明可靠性理论教学实施的步骤与方法。每个案例各有侧重，由浅入深地引出重要知识点，通过编程实践引导学生进行实例求解。基于案例启发式的教学模式可激发学生探求可靠性理论的学习热情，从而实现与专业问题相互衔接。

关键词：案例；可靠性理论；教学模式；编程

中图分类号：TU 473      文献标志码：A      文章编号：1005-2909（2024）03-0144-10

《工程结构可靠性设计统一标准》（GB 50153-2008）［1］实施多年，可靠性理论日渐成为较多高校土木工程专业三、四年级本科生或研究生的选修课程之一［2-3］。通过讲授可靠性理论的基本概念和求解方法，帮助学生认识土木工程中客观存在的不确定性现象［4］，力求掌握不确定性分析的建模方法。为了全面培养学生终身学习能力和实际问题处理能力，全新教学方法亟待提出。

可靠性理论是一门既具有理论性，又兼有较强应用性的课程。不仅要求学生具备土木工程专业基础知识，还需要学生具有足够的数学知识积累，如高等数学、概率论与数理统计、随机过程等。多数选课学生不具备类似基础知识而对可靠性理论产生陌生感，从而表现出学习吃力、学习意愿不强等问题［5］。这也是影响学生学习可靠性理论的外因。

难以有效开展可靠性教学的内因主要有：（1）讲授可靠性求解算法时与实际工程案例结合不够紧密，难以激发学生的求知欲；（2）教学偏重理论讲解和算法推导，缺少与编程演练相结合，学生缺乏学习动力，也无法在解算过程中获得成就感。

在有限课时内让学生掌握可靠性原理与方法，并自编程序分析与解决实际问题，是可靠性理论教学必须着力思考的问题。根据多年的教学经验，从实际工程问题的求解出发，提出以案例引导的课程教学方法。结合具体工程应用实例对相关计算理论深入讲解，引导学生开展实证学习。由浅入深地引出知识点并辅以编程演练，有助于培养学生解决不确定性问题的能力。

一、课程特点及教学现状

（一） 课程特点

（1） 理论抽象且方法繁多。可靠性理论课程教学主要内容包括概率密度分布、极限状态方程构建、可靠指标的定义与求解算法。其共同特点是抽象且难以理解。求解算法是可靠性理论课程的核心内容，通常包括一次二阶矩法、均值一次二阶矩法、改进一次二阶矩法与一阶可靠性法（first order reliability method，亦简称为FORM）等。面对众多算法，初学者难以在有限的授课学时内把握它们所蕴含的数学基础与原理，教师尝试讲解清楚各种算法之间的异同需要花费大量时间。

（2） 算法难以实现手工验算。工程中常用的一阶可靠性法，计算过程繁琐，需通过多步迭代才能得到收敛的结果；手工计算易出错且不可移植。

（3） 计算成果缺少图形展示。求解算法得到的数值结果具有一定的抽象性，缺少直观的图形解释。

（二） 教学现状

（1） 理论讲解与计算实施脱节。可靠性理论源于工程实践的统计分析与经验总结，部分理论公式涉及迭代或优化求解，计算工作量大。目前教学中比较重视理论知识的讲授，局限于理论公式的推导与代入，但对计算程序实施并未给予足够重视。

（2） 算例缺乏实际工程背景。教材中给出的算例多是高度简化的，缺乏实际的工程背景，难以充分激发学生学习可靠性理论的兴趣，学生难以与当前的研究课题进行有效衔接。部分教材的课后习题过于理想化与公式化，缺乏实际案例分析。

（3） 学生求知兴趣不高。可靠性理论的学习需要以数理统计、数值计算方法、编程等基础课程为基础，要求学生具有较好的数学功底。部分学生甚至不清楚所学课程与从事专业的关联性，学习目标不明确，投入的时间与精力不足。

（4） 生源基础参差不齐。由于地域不同且各生源高校间先修课程的教学内容有差异，刚接触该课程的学生对基础知识掌握程度不一，给可靠性理論课程的教学计划与教学组织带来较大的困难。

（5） 新版教材匮乏。与可靠性理论教学相关的教材更新速度较慢，在一定程度上制约了教学的有效开展。

二、案例启发教学法的特点

案例教学法是一种富有创意和实效的教学策略，它以教师与学生互动为基本形式，通过实际工程案例引导将复杂理论场景化，借助编程工具进行可靠性分析实现理论学习的生动化。该方法强调学生的参与。

案例教学实施三个阶段：课前准备、课堂实施和课后评估。课前准备阶段做好教学设计，精心选择案例并进行初步编程。在教师的引导下，采用互动与讨论式的教学手段提高学生的参与意识。教师提出问题，与学生充分互动，并引导学生编写求解代码，对学生发言与编程求解进行点评，从而提供分析问题的思路或视角。课后评估阶段主要针对作业完成情况和案例分析成绩进行评价。基于案例引导的可靠性理论教学有如下特点。

（一） 教学内容的案例化

教学案例可分为讲解型与探究型。讲解型案例通常只有一个核心论题；但探究型案例涉及面较宽，且案例通常能说明一个理论或算法。所选案例要有突出的目的性与代表性，围绕案例的起因、求解过程、安全评价等方面进行。表1为与可靠性理论课程教学大纲中规定的重点内容相关的几个案例。

绪论教学环节，重点介绍客观存在的观测数据、数据离散性的描述方法，以及边缘分布拟合等内容。协助学生梳理具有显著离散性的实测数据集，尤其是针对同一结构物或构件进行多次重复性测试的情况，类似成果更具有真实性。可让学生充分意识到不确定性问题发生在实践中。在介绍荷载的统计分析时，可结合简单的悬臂梁案例进行讲解，着重介绍一阶可靠性法中的Ang和Tang算法［6］；结合海堤漫顶案例对Low和Tang算法［7］、随机变量相关性处理及联合概率密度函数构建进行介绍。在结构抗力的统计分析这一教学环节中，可结合基桩静载响应成果，采用全新的几何可靠性可视算法［8-9］进行讲解。在介绍结构可靠性分析这一重要章节中，可针对板桩墙探究型案例，采用随机模拟法求解，并着重分析多种失效模式的关联性。

（二） 实际应用的关联化

在教学过程中，教师应注重应用实例与复杂概念的衔接。结合表1中悬臂梁、海堤、基桩和板桩墙等实际案例，充分与多种可靠性算法融合讲解，着力激发学生探求可靠性理论的学习热情。介绍工程背景与力学机理时，适当运用多媒体教学工具，展示图文音像等信息，并深入分析案例中蕴含的数据离散性来源与处理方法。

（三） 教学过程的编程化

在课程教学过程中，要求学生在初步了解基本概念的同时，借助各种编程语言的内部函数及现有的可靠性算法求解器［10］自行编写代码，开展多种算法的求解。从而实现在编程实践环节掌握并强化可靠性理论的知识点。

三、案例教学实质及授课思路

（一） 案例教学实质

案例教学的实质是讲授者本着理论联系实际的宗旨，针对相关教学内容，遵照教学目的，以案例为基本素材，将学生引入特定的真实工程情境中，鼓励学生积极参与，通过师生的双向交流，让学生充分理解复杂理论。

（二） 案例分析与讲授

每个案例讲授可控制在两个学时之内。基于可靠性理论，结构物需要完成预定功能，由功能函数或极限状态方程来描述。若为构筑物的抗力或允许承载，为作用效应或实际荷载。以构筑物的正常使用（承载能力）极限状态作为分析对象，二者构建的极限状态方程（功能函数）为：

（1）

结合特定案例分析，抗力以及作用效应可取决于多种影响因素，根据实际情况将某些因素视作随机变量。选择已建或新建工程项目作为案例进行深入剖析，由浅显知识点入手，逐步深入。工程案例应包括：a.工程背景与机理分析、荷载与输入参数（土层、地质、水位、气象）的收集与给定；b.绘制计算简图，确定结构物失效模式，构建极限状态方程；c.可靠指标的求解算法展示；d.输出结果判断与案例评价。

（1） 案例1：悬臂梁抗弯性。

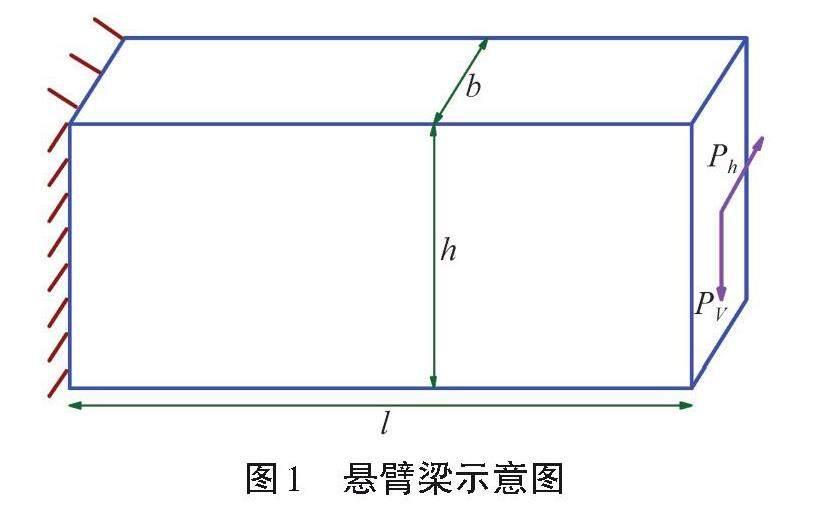
问题：矩形截面钢筋混凝土受弯悬臂梁，其截面宽度、高度以及跨度已知，如图1所示，试计算该构件用于住宅或办公楼时发生挠曲变形或强度屈服的可靠指标［11］。将悬臂梁构件所受到的垂直荷载Pv与水平荷载Ph作为随机变量，分别由给定的边缘概率密度函数来描述。

功能函数：若受弯构件发生挠度失稳，以构件挠度的实测值接近其限值为达到正常使用极限状态的标志，可建立极限状态方程。此外，悬臂梁构件若发生强度屈服，相应的极限状态方程可写为悬臂梁的最大屈服强度应力与实际应力之间的关系，亦可构建极限状态方程。

算法：一阶可靠性法基于随机变量服从正态分布的假设而构建。当用于非正态随机变量的情况时，采用Ang和Tang建议的一阶可靠性法时需考虑概率转换（当量正态化）等内容［6］。

关联知识与延伸：作为第一个案例，不宜给学生灌输过多的理论或概念。引导学生实现对荷载的统计特性以及非正态变量的处理，提供与演示Ang和Tang［6］算法的求解代码让学生自行尝试。教学过程中引导学生思考几个问题：a.非正态变量的当量正态化进行方式；b.若这些变量均服从正态分布时，求解的简化处理方式；c.其他可视作随机变量的参数；d.列举悬臂梁在土木工程中实际的应用场景。

教学中引导学生积极思考并发表观点，教师进行总结与评论。例如强调荷载比、配筋率、构件几何尺寸、混凝土保护层厚度等对可靠指标产生影响；随着构件装配化建造精度的提高，几何尺寸可被视作常量。通过该算例，向学生阐明可靠指标求解时涉及的迭代算法增加了计算实践的繁杂性，强调编程实施的必要性。

（2） 案例2：海堤漫顶。

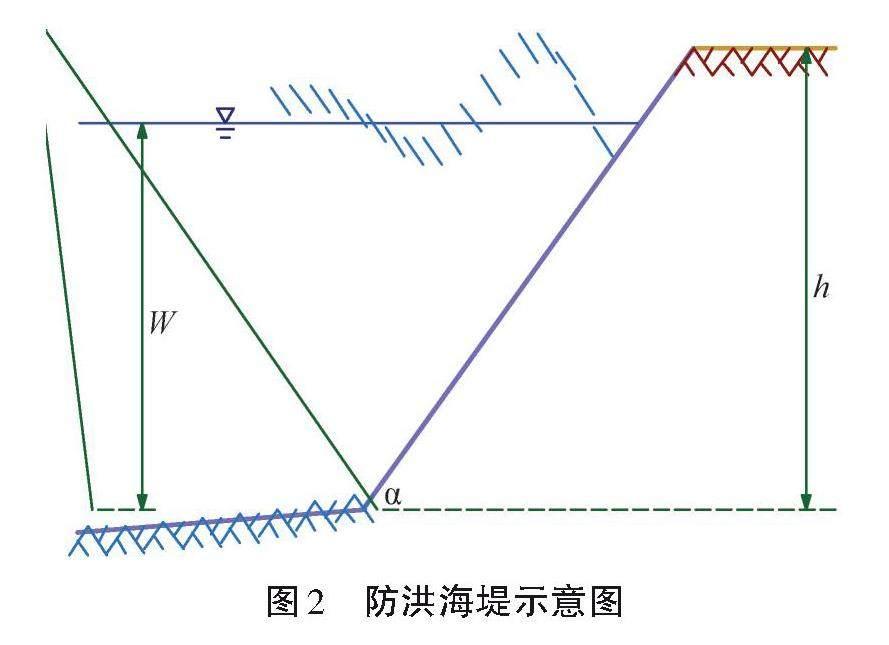
问题：海堤是防洪工程体系的重要组成部分，用于抵御风暴潮引起的海水漫顶，有效保护内陆的生命财产安全。海堤的防护通常与水位Hw、近岸有效波高Wh和平均波浪周期Tm在内的海洋風暴条件有关。图2为防洪海堤的示意图。由于近海波多通过卫星或雷达测量，实现了海洋学中观测数据的长期记录跟踪，开展海堤安全评价对海岸防灾减灾具有重要意义。

功能函数：海堤的极限状态方程可通过临界溢流量qc与海堤在一定时间段内的每延米的溢流量qw之差表示［8］。有限的越浪量不会造成大面积的洪灾，但漫顶会引起堤顶侵蚀以及下游坡的冲刷从而最终造成海堤破坏。溢流量取决于波浪爬高、风壅高度、堤顶高程、水位等因素，其中，波浪爬高又与波浪高度以及周期密切相关。溢流过程由风暴潮位和波浪共同作用引致，在时间和体积上是较随机的现象，故将水位Hw、波高Wh和周期Tm视作随机变量。

数据：海堤断面位于英国Norfolk地区，共整理了十年内该海浪要素的7 030组观测数据［8］。图3为三个随机变量间的相依关系以及各个变量的核概率密度分布。

算法：结合该算例，重点讲授其他一阶可靠性算法。该算法的几类演变方法，如修正一次二阶矩法或JC法［12］、Low和Tang的［7］求解模式等，需要重点讲授。

关联知识与延伸：重点剖析可靠性算法的几个要点，尤其是非正态分布的处理以及双变量联合概率密度函数的构建与算法原理。在多元随机变量联合分布中，各变量间存在一定的相关性，且各变量的边缘分布类型也不尽相同。对于随机变量的联合概率分布，可由联结函数Copula构造［13］。授课中，对学生强调此研究是可靠性研究的热点，引导学生深入探究。

结合该典型工程案例，教师从问题提出、计算分析和成果评价等方面引导学生全面了解基于可靠性理论的求解过程。在课堂上与学生一起讨论离散性对海堤稳定性的影响，尤其是联合分布的尾部特征，充分调动学生分析和思考问题的积极性。考虑该海堤其他潜在失效模式，如边坡滑动失稳、管涌、冲刷等，也值得学生探讨。

（3） 案例3：基桩承载性能。

问题：桩基础通过桩侧摩阻力和桩端阻力将上部荷载传递到深部岩土层中，有效提高多层建筑地基的承载能力，减小地基沉降并确保上部结构安全。受到同一场地内地层空间变异、桩体施工与测量误差等一系列因素的影響，多根基桩承载后的沉降数据是离散的。

以山东省济南市一栋28层公寓楼场区内预制方形桩的荷载-位移数据进行分析［14］。该场地共计完成12根工程桩的检测，最大加载为4 880 kN。桩的边长为0.4 m，桩长22～28 m。图4为竖向静载试验得到的荷载-位移曲线。采用幂函数进行每条测试曲线的拟合［9］，列式为：

（2）

荷载-位移关系是各层土体与桩之间摩阻特性的综合反映，构建幂函数回归方程后，由最初需要考虑桩周各层土体侧摩阻与持力层端摩阻特性的多元随机性，转化为直接讨论幂函数回归参数间的不确定性，使得多元论题被简化为二元变量间的问题。

由于同一场地下测试得到的12条曲线形态各异，描述这些曲线特性的回归参数集必然具有离散性。图5为幂函数回归和集合的散点分布，且分别将二者视作一个随机变量。若假定p1和p2均服从正态边缘分布，且存在线性相关系数，则其特定置信水平下联合分布（二元高斯分布或称作二元正态分布）的概率密度等值线（probability density contour，简称PDC）为椭圆形状［15］。

功能函数：基桩相应的正常使用极限状态方程可表述为承载能力与上部结构传至桩顶荷载之间的关系。式（2）中基桩抗力R可由p1sa p2定义，sa为基桩沉降量的容许位移值。基桩实际荷载（作用效应）S可假定为常数或定值，可取为最大加载量值的1/2。

数据：基于国内外30余个场地下基桩荷载-位移曲线的回归参数集［16］，让学生尝试特定场地下其他基桩承载能力的可靠性评估。

算法：从几何上看，一阶可靠性法中定义的可靠指标是在多元标准化空间中由坐标原点到临界破坏面的最短距离，该指标亦称为Hasofer-Lind指标［17］。常规的可靠性理论因构建于标准化空间内，公式推演较为深奥。本研究团队开发的几何可靠性算法［8-9］构建于随机变量的原始物理空间内，更易于理解。根据几何可靠性算法，对于二元正态联合分布，该建筑场地下基桩（构筑物）承载能力的可靠指标将由单倍标准差椭圆和发散椭圆之间的比例关系给定，如图5所示。极限状态曲线由功能函数推求得到，将随机变量所在区域分为安全域与失稳域。

关联知识与延伸：尽管该案例的功能函数看似简单，但具体求解时会遇到较多知识点；a.其他随机变量如何考虑，若考虑基桩所受荷载的随机性，如分别将恒载与活载也视作随机变量，它们与回归参数集构成四元随机问题，采用几何可靠性算法进行求解的方式；b.非正态分布如何考虑。该算法因采用离散点近似表征各种构型，具有适用于各种非正态联合分布的灵活性；c.剖析基桩的承载能力极限状态与正常使用极限状态［9］，其定义式异同点与关联性值得师生互动研讨；d.传统定值安全系数由变量的期望均值（图5）给定，无法考虑随机变量的统计特性或规律。结合案例阐释概率极限状态设计有别于传统确定性设计。概率极限状态设计强调变量的观测与统计，而确定性设计更多地依赖于经验。极限状态设计在构建极限状态方程时为继承确定性安全系数的定义式。总之，结合具体工程应用，对可靠性理论实施图形化解译，给予学生切实的掌控体验，可克服常规可靠指标求解时采用各种方程的抽象感。

（4） 案例4：板桩抗倾覆性能。

问题：板桩结构多用于码头与基坑等支护体系中［10］，图6为拉锚式板桩墙示意图。板桩墙的抗弯强度和踢脚稳定均与土体的抗剪特性密切相关。土性参数（粘聚力、内摩擦角、容重）的不确定性、墙后堆载、地下水位变化、板桩材料、拉杆抗拉强度等均会影响板桩结构可靠性。为了保证毗邻建筑物的正常使用，板桩在其设计使用年限内应具有足够的可靠性。

数据：若考虑土体剪切强度参数（粘聚力与内摩擦角）对板桩结构的影响，结合20余个场地下土体的抗剪强度参数集［16，18］，可进行相关问题的不确定性分析。

功能函数：考虑抵抗力矩与实际承受力矩之间的关系可构建踢脚（抗倾覆）稳定的极限状态方程。

算法：随机抽样法为估算失效概率的常用方法。失效概率是随机模拟中功能函数小于零的次数与总模拟次数之比。考虑随机变量间的互相关性时，可采用基于联结函数的抽样法（Copula-based sampling method，简称CBSM）［13］求解失效概率。但该类方法存在计算结果不唯一且在失效概率较低情况下计算工作量大的缺点。授课教师应说明随机抽样法计算得到的是失效概率值，两次计算可能会出现失效概率在数量级上的差异结果。而其他非抽样类算法计算得到的是可靠指标，最常用的量值介于0～8之间。该指标与失效概率相比更易于被工程师接受。鼓励学生采用非抽样类方法完成该案例的求解，以便比较各种算法的计算成果。

关联知识与延伸：该案例比较综合，要引导学生区分哪些变量与抗力有关，哪些变量与作用效应有关。应该指出，板桩墙后的主动土压力为作用效应，而板桩墙前的被动土压力则为抗力。这些土压力均因土体参数的不确定性而具有随机性。授课过程中先对学生提出问题，然后让学生选边站队并充分辩论，以明晰最终结论。

教师需向学生解释该案例的相关应用场景，鼓励学生通过文献查阅更多实际案例。同一个板桩墙问题，可以是建筑基坑问题，也可以是码头支护问题。码头堆载因运输发生变化，板桩水平向荷载还涉及波浪力。此外，板桩墙抗弯、拉杆抗拉、坑底抗隆起、整体滑动稳定等也可作为失效模式进行分析，多种失效模式的关联性需详细剖析。

（三） 编程实施

提及的算法可采用Matlab、R、Python或Mathmatica语言进行编程实施，教学中尽可能地增加编程环节。教师运用编程平台结合求解算法进行计算展示，统筹实施课程教学，保证课堂教学的有效组织。编程语言具有丰富的绘图功能与科学计算函数，比如，算法中涉及的散点图、曲线图等均可由相应函数实施。采用高级编程语言，多数工程实例仅需20余行代码即可完成所有计算与绘图。编程实践有助于培养与提高学生的自主创新与问题求解技能，在課堂实践环节与课后作业巩固方面均需有所侧重。

讲授时要给学生强调编程实施的优势在于方便修改任意参数，快速而准确地求解并进行参数敏感性分析。鼓励没有任何编程基础的学生尝试电子表格法编制Excel表实施，更能适应现代信息化社会需求。引导学生进行可靠性算法函数的编写，以便更多成熟算法共享给工程师使用，让学生在研学实践中获得成就感，激发他们对更复杂专业问题的探索兴趣。

此外，教学实施中还可结合Visual Basic开发面向对象的基桩几何可靠性分析软件［19］。学生通过菜单化操作该认知工具，深化对可靠性理论的理解。

四、常见问题的讨论与分析

（一） 案例教学实施对教师的要求

案例教学对授课教师的综合素质要求较高，需要将案例提升到理论层次，且要熟练掌握编程技能。在课前要准备充分，预习教学素材、熟悉案例、归纳重点与难点，以及认真编写教案。

（二） 源代码准备

每个案例的编程及验证一般较为耗时，但课堂时间非常有限，这要求教师提前准备与精心构思预备部分程序（源代码）并提供给学生。强调采用丰富库函数的高级编程语言的重要性，以便让学生从繁琐的基础程序代码中解放，更多地专注于可靠性算法的编程实践。

（三） 教材选用

教师难以在同一本教材或者文献中找到多学科关联的素材，建议使用自行整理的讲义进行授课。教师列出一系列参考资料，供学生课后深入阅读参考。

（四） 案例教学法的缺点

案例教学较难通过案例说明整体原理，难以将获得的概念与原理汇总于一个整体框架中。因此，要求学生通过深入学习，厘清各个知识点间的关联性。课后教师需要强调延伸阅读的重要性，使学生找到分析此案例的理论支持和必要知识点。

（五） 其他问题

教学中可引导学生采用多种算法求解同一问题，结合自己的专业背景进行选题，更容易让学生实现由可靠性基本原理学习向探究自己专业课题的过渡。阐明不同问题对于随机变量值域的要求不同。如漫顶问题与波浪条件的极大值密切相关，而土工强度问题则取决于强度参数的极小值。任何结构物的可靠性设计均基于观测数据，若没有更多重复性的实际观测成果，再好的可靠性计算模型也将被束之高阁。

五、结语

结合可靠性理论课程实践性和应用性强的特点，通过生动的工程案例提高学生的学习兴趣。案例教学模式能促进学生有针对性地运用专业理论，提高其分析与解决实际不确定性问题的能力。从教学内容、编程环节、案例与理论的关联度、教学方法等方面，对课程教学进行了全面的总结与思考。

课堂教学中结合多个不确定性评估的应用场景，针对可靠性方法的演示与编程实践，让学生熟悉编程环境并有助于消除学生的畏难疑虑。与常规教学方法相比，采用实际案例进行启发式教学，实施简洁且更易于实现深层次的概念延伸。尽管案例教学法使教学内容更加丰富而生动，避免了教师纯粹理论性的说教，但是在实践应用中也存在一些问题，需要在实践中探索解决方案。

参考文献：

［1］ 中华人民共和国住房和城乡建设部.工程结构可靠性设计统一标准：GB 50153—2008［S］.北京：中国计划出版社，2009.

［2］ 李会军，李宗利.工程结构可靠度分析课堂教学的改革与实践［J］.黑龙江教育（高教研究与评估），2019（3）：1-3.

［3］ 张振浩，杨伟军.“荷载与结构设计方法”课程教学方法研究［J］.中国电力教育，2012（11）：78-79，84.

［4］ 吴兴征，方有亮，余莉，等.土工试验教学中如何培养学生的不确定性思维［J］.高等建筑教育，2019，28（3）：122-130.

［5］ 贾传果，李英民，夏洪流，等.荷载与结构设计课程教学问题及解决对策——以JCSS组合规则为例［J］.高等建筑教育，2014，23（4）： 92-95.

［6］ Ang H S， Tang W H. Probability Concepts in Engineering Planning and Design， Vol. II. Decision， Risk， and Reliability［M］. New York： John Wiley and Sons， 1984.

［7］ Low B K， Tang W H.Efficient spreadsheet algorithm for first-order reliability method［J］.Journal of Engineering Mechanics， 2007，133（12）：1378-1387.

［8］ Wu X Z. Geometric reliability analysis applied to wave overtopping of sea defences［J］.Ocean Engineering，2015，109： 287-297.

［9］ 吴兴征，王瑞凯，辛军霞.特定场地下土工构筑物的几何可靠性分析［J］.岩土力学，2020，41（6）：2070-2080.

［10］ Wu X Z.Implementing statistical fitting and reliability analysis for geotechnical engineering problems in R［J］. Georisk： Assessment and Management of Risk for Engineered Systems and Geohazards，2017，11（2）：173-188.

［11］ Wu YT， Wang W. Efficient probabilistic design by converting reliability constraints to equivalent approximate deterministic constraints［J］. Journal of Integrated Design and Process Sciences， 1998， 2（4）：13–21.

［12］ Rackwitz R，Flessler B.Structural reliability under combined random load sequences［J］.Computers & Structures，1978，9（5）：489-494.

［13］ Wu X Z. Probabilistic slope stability analysis by a copula-based sampling method［J］.Computational Geosciences，2013，17（5）：739-755.

［14］ Zhou J L.Behavior of displacement concrete pile under compressive loads［J］.International Journal of GEOMATE， 2019，16（54）：200-208.

［15］ Wang B， Shi W Z， Miao Z L. Confidence analysis of standard deviational ellipse and its extension into higher dimensional euclidean space［J］.PLoS One，2015，10（3）：e0118537.

［16］ Wu X Z.GeoRiskR： data and functions for geotechnical risk assessment［EB/OL］.［2021-11-10］. https：//r-forge.r-project.org/R/？group_id=1777 or http：//xingzhengwu.com/downl/GeoRiskR2.1.pdf.

［17］ Hasofer A M， Lind N C. Exact and invariant second-moment code format［J］.Journal of the Engineering Mechanics Division， 1974， 100（1）： 111-121.

［18］ Wu X Z.Modelling dependence structures of soil shear strength data with bivariate copulas and applications to geotechnical reliability analysis［J］.Soils and Foundations，2015，55（5）：1243-1258.

［19］ 吴兴征.基桩静载数据处理与可靠性分析软件开发及应用［J］.工程質量，2021，39（3）： 10-16.

A teaching model for the reliability theory by illustrative case studies

WU Xingzheng1， WANG Ruikai2， SONG Pengyan1

（1.College of Civil Engineering and Architecture， Hebei University， Baoding 071002， P.R.China；

2.College Electronics & Information， Hengshui University， Hengshui 053010， P.R.China）

Abstract： Formula derivation is emphasized and case study is neglected in the traditional teaching for the reliability theory， resulting in low teaching efficacy. The teaching technique through illustrative case studies is proposed， and the importance of both case teaching concept and learning promoted by programming is stressed. Four typical case studies， such as the cantilever beam， sea dike， pile foundation， and sheet pile wall， are implemented to explore the procedures and methods for the teaching of reliability theory. Each case study has its own emphasis on the teaching content， leading to key knowledge components from the easy to the difficult， which allows students to immerse themselves in the solution of examples through programming practice. The teaching model based on case heuristics is easy to stimulate students enthusiasm for exploring the reliability theory， and it is easy to realize the connection with professional problems.

Key words： case; reliability theory; teaching model; programming

（责任编辑  邓  云）