温度场下功能梯度圆锥壳-环板振动特性分析

左朋, 石先杰

(1.中国工程物理研究院 总体工程研究所,四川 绵阳 621999; 2.中国科学技术大学 近代力学系,安徽 合肥 230026)

功能梯度材料(functionally graded material, FGM)通常由陶瓷和金属组成的混合物制成,以获得在一个或多个空间方向上具有渐变特性的功能性能。圆锥壳、环板以及圆锥壳-环板组合结构在火箭、飞行器、潜艇等装备中被广泛应用,例如飞行器头部、潜艇艉部等。因此,FGM圆锥壳-环板组合结构振动特性逐渐成为学者们的研究热点,并在过去几十年里取得了较为显著的成果,并提出了一系列数值解法,如改进傅里叶级数法[1-5]、拟格林函数法[6]、微分求积法[7-10]以及无网格法[11]等。

此外,功能梯度材料克服了传统材料的缺陷,具有耐高温性能。因此,温度场作用下的FGM结构振动特性研究也一直是研究热点。Malekzadeh等[12]采用微分求积法求解了热力控制方程,获得了温度场影响下的FGM圆锥壳三维自由振动特性。在二维弹性理论以及Hamilton变分原理框架内,滕兆春等[13-14]推导了温度场作用下FGM薄环板面内自由振动控制方程,并采用微分求积法有效地求解了环板结构的振动频率特性。吕朋等[15]在平面弹性理论框架内推导了温度场影响下FGM薄环板的面内振动能量方程,并应用改进傅立叶级数法求解获得了面内自由振动特性。考虑沿厚度方向的非线性温度分布,Mirtalaie[16]在经典板壳理论基础上,推导并建立了FGM薄环扇形板自由振动控制微分方程,并用微分求积法求解获得了自由振动特性。在一阶剪切变形理论框架下,Chen等[17]分别采用切比雪夫多项式和傅立叶级数表示壳段和环板的位移函数,研究了温度场影响下FGM阶梯圆柱壳-环板组合结构的振动特性。

综上可知,现有大多数研究是针对单一的圆锥壳或者环板结构振动问题,关于圆锥壳-环板组合结构的振动特性研究却少有涉及。随着产品结构朝着轻量化方向发展,FGM结构的轻量化和力学性能可设计等显著特征使得FGM圆锥壳-环板组合结构在火箭、飞行器等回转类装备结构设计中得到广泛应用。

本文考虑材料参数与温度相关,在一阶剪切变形理论框架内推导获得了FGM圆锥壳以及环板结构的能量方程表达式。利用人工边界弹簧模拟圆锥壳、环板的边界约束条件及组合连接关系。采用谱几何法建立了温度场影响下FGM圆锥壳-环板组合结构振动特性分析模型。在数值算例中,通过将本文求解结果与文献解和有限元法结果进行对比,验证了所构建模型的正确性,并进一步分析了相关重要参数对FGM圆锥壳-环板组合结构自由振动特性的影响规律。

1 FGM圆锥壳-环板组合结构振动分析模型

1.1 FGM圆锥壳以及环板结构能量方程

图1(a)和(b)分别是FGM圆锥壳以及环板结构模型示意图,其中环板是圆锥壳半顶角θ=90°时的特殊情形。其中O为坐标原点,符号ζ=c,a为表示圆锥壳以及环板结构,(αζ,βζ,zζ)为建立在对应结构的中性面zζ=0处的正交坐标系。h为结构沿zζ方向的厚度,Lc为圆锥壳结构沿αc方向的长度。R0c和R0a分别为圆锥壳的小端圆半径以及环板的内径,而R1c和R1a则分别为圆锥壳的大端圆半径以及环板的外径。Uζ=(Uζ,Vζ,Wζ)T上任一点沿(αζ,βζ,zζ)方向的位移。基于一阶剪切变形理论,位移变量为:

(1)

图1 圆锥壳以及环板结构模型

式中:uζ=[uζ,vζ,wζ,φαζ,φβζ]T为结构中性面处的位移向量,其中[uζ,vζ,wζ]T表示的是沿[αζ,βζ,zζ]方向的平移位移,而[φαζ,φβζ]T则对应的是绕β和α轴的旋转位移。

基于小变形理论和线性应变-位移关系,结构上任意点的应变分量(εαζ,εβζ,γαβζ,γαzζ,γβzζ)为:

(2)

根据FGM板壳结构的力和力矩方程,可以得到矩阵形式表达式:

(3)

式中,Nζ=[Nαζ,Nβζ,Nαβζ]T是结构的面内合力向量,Mζ=[Mαζ,Mβζ,Mαβζ]T对应的是结构的力矩向量,而Qsζ=[Qαζ,Qβζ]T表示的是横向剪切力向量。κ=5/6为剪切修正参数。A、B和D为拉伸、拉伸-弯曲组合和弯曲刚度参数Ajk、Bjk和Djk组成的矩阵,具体表达式参见文献[18]。Ajk、Bjk和Djk为:

(4)

式中:Qij是材料刚度系数,为厚度z和温度T的函数,并与材料弹性模量E、泊松比μ等参数有关,其表达式参见文献[19]。此外,本文研究还涉及到热膨胀系数αT以及质量密度ρ等材料参数,上述材料参数C与温度T的关系为:

C(T)=C0(C-1T-1+1+C1T+C2T2+C3T3)

(5)

式中:C0、C-1、C1、C2和C3为温度相关系数,材料不同,其取值也各不相同。另外,功能梯度材料通常由2种材料混制而成,其材料参数C与厚度方向z关系为:

(6)

式中:p为材料的幂律指数;Cz0和Cz1分别为圆锥壳内表面(或者环板下表面)以及圆锥壳外表面(或者环板上表面)的材料参数。

基于线弹性理论,FGM圆锥壳以及环板的结构势能Upζ为:

(7)

由于本文考虑了温度环境对结构动力学特性的影响,因此需要考虑引入温度场时所产生的附加热势能UTζ,为:

(8)

式中ΔT=T-T0表示的是结构温度值T与参考温度值T0之间的温度变化值。

相应地,FGM圆锥壳以及环板的结构动能TKζ为:

(9)

1.2 组合结构能量方程及求解

在获得FGM圆锥壳以及环板结构能量方程的基础上,进一步建立温度场下FGM圆锥壳-环板组合结构的振动特性分析模型,如图2所示,其中符号pc表示的是环板在圆锥壳上的连接位置,故有R1a=R0c+pcsinθ。

图2 圆锥壳-环板组合结构模型

本文采用人工边界弹簧模拟圆锥壳、环板的边界约束条件以及组合连接条件[18]。用下标0、1和a0分别对应圆锥壳小端边界、圆锥壳大端边界和环板内边界,组合结构的边界势能VB为:

(10)

其中,k=diag(ku,kv,kw,kα,kβ)分别为约束位移分量uζ=[uζ,vζ,wζ,φαζ,φβζ]T的弹簧刚度值。

下标c为耦合位置处的弹簧刚度,则组合结构的耦合势能Vc为:

kcv(va|α=R1a+vc|α=Roc/sin θ+pc)2+

kcw(wa|α=R1a-(uc-wc)α=Roc/sin θ+pccosθ)2+

kcα(φαa|α=R1a-φαc|α=Roc/sin θ+pc)2+

kcβ(φβa|α=R1a-φβc|α=Roc/sin θ+pc)2]dβ

(11)

式中:kcu、kcv、kcw为约束平移位移的线性耦合弹簧刚度值;kcα、kcβ为约束旋转位移的扭转耦合弹簧刚度值。

综上,温度场下FGM圆锥壳-环板组合结构的拉格朗日能量方程为:

(12)

由于圆锥壳以及环板结构位移向量在周向方向上对称,可将其沿β方向的位移分量采用正余弦级数展开,同时将其沿α方向的位移分量采用谱几何法[20]展开,位移向量展开式进而可表示为:

(13)

将式(13)代入式(12),并采用Rayleigh-Ritz法[20-21]对未知级数展开系数求偏导,即可获得温度场下FGM圆锥壳-环板组合结构振动分析模型:

(K-ω2M)H=0

(14)

式中:K和M分别表示组合结构的刚度矩阵和质量矩阵;H为未知级数展开系数向量矩阵。

2 数值算例与分析

本文利用振动分析模型进行温度场作用下FGM圆锥壳-环板组合结构自由振动特性分析。由于参考文献[18]中对弹簧刚度值的收敛性进行了充分分析,因此本文将组合结构单位长度的弹簧刚度值设为:kcu=kcv=kcw=kcα=kcβ=1014N/m。本文可以通过设置不同弹簧刚度实现与之对应的边界条件,其中自由F、第1种简支S1、第2种简支S2以及固支C边界条件的弹簧刚度值设置如表1所示。用横线连接字符的形式来表示组合结构所受到的边界条件,如C-S1-F表示组合结构的左边界为固支,右边界为第1种简支,环板内边界为自由。此外,除非特殊说明,本文FGM圆锥壳-环板组合结构几何参数设置为:h=0.05 m,θ=30°,R0c=0.5 m,Lc=4 m,R0a=0.2 m,pc=Lc/2;温度场参数设置为:参考温度值T0=300 K, 结构温度值T=300 K。

表1 不同边界条件对应的每组边界弹簧的刚度值

2.1 模型验证

图3所示为C-C-C边界下圆锥壳-环板组合结构在不同级数截断数M下第1、2、4、6阶的频率参数收敛曲线。圆锥壳内表面以及环板下表面的材料为金属304不锈钢,圆锥壳外表面以及环板上表面的材料为陶瓷氮化硅,幂律指数p=1,材料温度相关系数见文献[19]。图中截断误差的定义为取M=30下的频率结果为参考值,其他级数截断数下的频率结果与参考值之间误差的绝对值。通过图3可知,各阶频率参数的截断误差在M=24后便基本保持不变,此时计算结果已经趋于收敛。因此,在后续算例中,截断数统一选取为M=26。

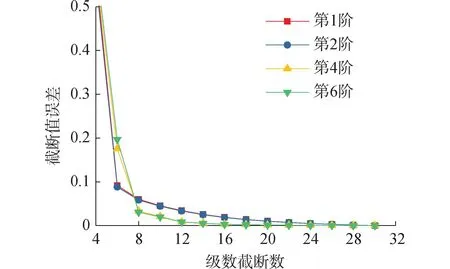
图3 不同级数截断数M对FGM圆锥壳-环板组合结构自由振动频率的影响规律

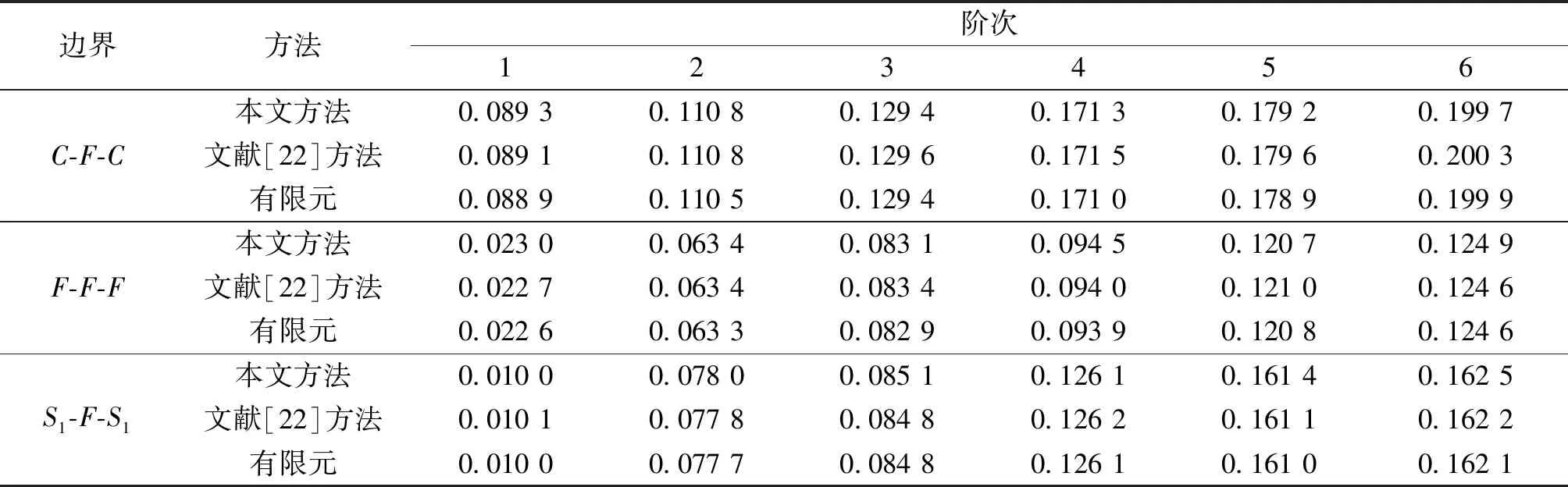
表2 圆柱壳-环板组合结构的前6阶无量纲固有频率对比

表3所示为考虑温度场影响的FGM圆锥壳-环板组合结构在C-C-C、C-F-C以及S2-S2-C边界下前7阶固有频率参数。材料参数及温度相关系数与图3算例保持一致,幂律指数p=1,2。由于此类FGM组合结构振动特性研究的公开文献较少,因此仅与有限元法结果进行比较分析,通过对比可以发现,本文方法的计算结果与有限元法结果吻合较好。为了更好地展现本文方法有效性和适用性,图4给出了C-F-C边界下组合结构模态振型对比情况。从图4可以看出,本文方法不仅可以准确预测固有频率参数,还可以获得结构模态振型。综上所述,本文构建的FGM圆锥壳-环板组合结构振动分析模型能够有效预测温度场作用下FGM圆锥壳-环板组合结构的自由振动特性。

图4 温度场影响下FGM圆锥壳-环板组合结构前5阶模态振型对比

2.2 参数研究

在验证本文构建分析模型有效性基础上,开展了FGM圆锥壳-环板组合结构自由振动特性参数化研究。

图5所示为结构厚度h以及材料幂律指数p对FGM圆锥壳-环板组合结构基频的影响规律。h的变化区间为[0.02 m, 0.1 m],p从0递增至10,边界条件定义为:C-C-C、C-C-S2以及C-C-S1,其余结构参数以及温度场的设置均与默认参数保持一致。从图5可知,结构基频随厚度h的增加可以明显提高,而随着幂律指数p的递增会呈现下降的趋势。

图5 结构厚度h和材料幂律指数p的变化对FGM圆锥壳-环板组合结构基频的影响规律

图6所示为环板内径R0a以及结构温度值T的变化对C-C-C、C-C-S2以及C-C-S1边界下FGM圆锥壳-环板组合结构基频的影响规律。R0a从0.05 m递增至0.5 m,T从300 K变化至400 K,其余参数与图4算例参数保持一致。从图6可以看出,保持参考温度值T0不变,结构基频随着温度值T的增加而逐渐降低,随着环板内径R0a的递增会呈现先显著增大后缓慢变化的趋势。

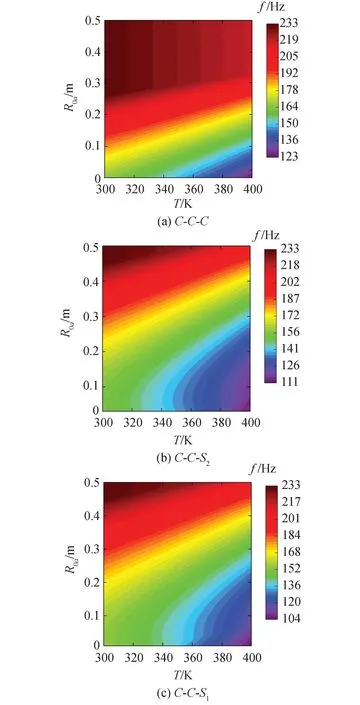
图6 环板内径R0a和结构温度值T的变化对FGM圆锥壳-环板组合结构基频的影响规律

图7所示为圆锥壳半顶角θ以及环板组合连接位置pc的变化对C-C-C、C-C-S2以及C-C-S1边界下FGM圆锥壳-环板组合结构基频的影响规律。半顶角θ的变化区间为[30°, 60°],pc从1 m向右移动至3 m,其余参数与图4算例保持一致。从图7可以看出,圆锥壳半顶角θ的增加会降低组合结构基频。而随着环板组合连接位置pc向右移动,组合结构基频会呈现先上升后下降的趋势,在C-C-C边界条件下,基频在pc=1.9 m时达到最大,而对于C-C-S2和C-C-S1边界条件而,基频最大值出现在pc=1.7 m时。

图7 半顶角θ和组合位置pc的变化对FGM圆锥壳-环板组合结构基频的影响规律

3 结论

1) 谱几何法具有良好收敛性和计算精度,且通用性好,当结构材料或者几何参数发生变化时,只需要修改相关初始参数即可,无需繁琐推导公式,简洁高效。

2) FGM圆锥壳-环板组合结构基频随厚度增加会呈现上升趋势,随着幂律指数、半顶角和温度场参数增加会呈现下降变化趋势。

3) FGM圆锥壳-环板组合结构基频随环板内径R0a的递增会呈现先显著增大后缓慢变化的趋势,随环板组合连接位置pc会呈现先上升后下降的趋势。