刚性薄平板绕流特性的数值模拟

蔚杰, 武建军

(兰州大学 土木工程与力学学院,甘肃 兰州 730000)

平板绕流是一类钝体绕流现象,广泛存在于自然界,如风对植物叶片的绕流[1-2]。平板也是一种常见的工程构件,大量应用于船舶工程、能源动力工程、仿生设计等领域,如水面推进器的旋转叶片[3-4]、海洋平台垂荡板[5]、核反应堆中的板状燃料组件[6]、仿生飞行器的扑动翼板[7-8]。平板构件周围流体的流动特性直接影响着平板的稳定性以及使役性能,甚至决定着装置中其他结构的设计。平板绕流系统还涉及复杂的转捩过程与流动分离现象,尚未被完全揭示的流动机理,使得对该问题的研究具有广泛的学术价值和工程实践意义。与圆(椭圆)柱绕流的可变分离点不同,垂直平板绕流的分离点固定,位于平板边缘。此外,由于剪切层不能重新附着于平板尾部,垂直平板近壁尾流的初始涡卷以及涡分离过程与其他钝体绕流存在明显差异,而且层流到湍流的转捩过程发生在尾流区而非分离剪切层[9-10]。平板周围的非定常流动包含2个主频,除了与Krmn涡街对应的频率外,还具有低频不稳定的流动特征。平板扁平的几何特征使得其具有较大的阻力系数[11],低频周期内,平板在高平均阻力状态和低平均阻力状态之间反复切换[12]。剪切来流绕流各类钝体时,来流与固壁边界层相互作用,形成了多种尾涡脱落模式,影响了流场由层流发展到湍流的转捩过程,而尾涡脱落频率、涡流强度也依赖于来流剪切梯度[13-14]。此外,结构承受多频特征的流体载荷,甚至诱发复杂的自激振动现象[15-18]。剪切来流绕流钝体的问题中包含了更为丰富的物理现象,其中所涉及的动力学问题值得深入的研究。另一方面,相比其他钝体结构,平板绕流受到的关注较少,特别是平板弦厚比L/t极大的情况。

本文采用浸没边界-格子Boltzmann方法(IB-LBM)对垂直薄平板的绕流问题进行了数值模拟。研究了雷诺数、来流剪切梯度对平板尾流涡街演化规律以及平板阻力特性的影响。

1 力学模型与数值方法

1.1 力学模型

如图1所示,长度为L的刚性薄平板被固定在二维粘性不可压流场中;假设薄平板厚度t远远小于长度。坐标原点位于平板中点,x轴与平板法向重合,z轴与平板切向重合。计算域42L×22L,平板距入口边界11L。

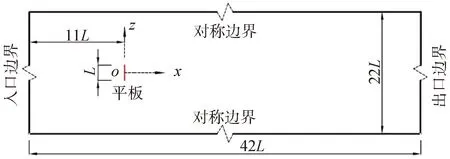
图1 计算域与边界条件

1.2 控制方程

对于长度L远远大于厚度t的刚性平板,由于绕流结构最小尺寸的限制,若采用全因素建模并结合贴体网格的计算方式,则需要在平板周围划分了大量的计算网格。浸没边界-格子Boltzmann方法(IB-LBM)通过引入体力项fv描述固体边界与流体间的相互作用,将边界产生的拉格朗日力插值并分配给周围的 Euler节点,并采用LBM对流场域进行求解。如图2所示,受文献[19]的启发,以一维固壁边界等效薄平板并将其离散为一组拉格朗日点集。薄平板绕流问题即可转化为对含外力项LBE方程的求解。此外,可以用几何形状规则的Cartesian网格对计算域进行离散。该方法有效地简化了此类平板绕流问题的求解过程。

图2 平板绕流问题浸没边界原理局部示意

含外力项的LBE方程[20]:

fα(r+eαδt,t+δt)-fα(r,t)=

(1)

(2)

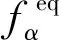
本文采用D2G9模型[21]作为离散速度模型,该模型以压力作为独立变量,速度配置为:

(3)

平衡态分布函数为:

(4)

(5)

解得粒子分布函数后,速度和压力可得:

(6)

(7)

式中密度ρ0为常数。

常用的浸没边界法[22-24]存在无法精确满足无滑移边界条件的固有缺陷。Wu 等[25]提出了基于隐式速度修正的浸没边界格子Boltzmann方法 (implicit velocity correction-based immersed boundary-lattice boltzmann method)。将式 (6)中的速度u分解为:

u=u*+δu

(8)

式中:u*为未经修正的速度;δu为修正速度。该方法将体力fv作为未知量,并通过隐式求解速度u的方式使得拉格朗日边界点满足无滑移边界条件:

(9)

ρ0δu=(fvδt)/2

(10)

对于图2中,拉格朗日边界Γ上的离散点XB(sk)(k=0,1,…,N),引入修正量δuB并将其设为未知量,Euler节点的修正速度δu可由δuB插值得到:

(11)

(12)

式中:D为Delta函数;核函数δ(r)取为:

(13)

将式(12)代入式 (11)得:

(14)

拉格朗日边界点速度UB由Delta函数插值得到,且需满足无滑移边界条件:

(15)

将式 (8)、(14)代入式 (15)可得:

(16)

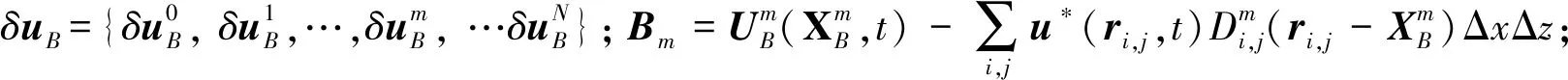
作用于固壁边界的流体力fb为:

fb=-2ρ0δuB/δt

(17)

由此可得结构的阻力、升力为:

(18)

进一步,阻力系数与升力系数分别被定义为[26]:

(19)

1.3 计算域离散

标准格子Boltzmann方法只允许在均匀网格系统中完成迁移-碰撞步,存在网格生成量大、计算精度不可调的缺点。为了提高计算效率,本文以非均匀网格对计算域进行离散,并根据泰勒展开和最小二乘格子Boltzmann方法(Taylor series expansion-and least square-based lattice Boltzmann method, TLLBM)对粒子分布函数进行求解,TLLBM的原理与实现方法可参照文献[27]。

如图3所示,直线x/L=±1,z/L=±1将计算域分为9个子区域,以映射网格技术生成网格。图中分以数字(1)～(9)对子区域1～9进行标识。子区域5采用均匀网格,Δx0=Δz0=L/80;浸没边界位于(5)中。其余各子区域的最小网格尺寸Δxmin=Δzmin=Δx0;子区域1、子区域2、子区域4、子区域7、子区域8最大网格尺寸Δxmax=Δzmax=2.2Δx0,子区域3、子区域6、子区域9最大网格尺寸Δxmax=Δzmax=3.0Δx0。计算域网格数:1 860×1 160。

图3 计算域分区策略与局部网格示意

1.4 数值验证

本文采用C++结合OpenMP并行技术编写计算程序,为了验证数值方法与程序的可靠性,对二维圆柱绕流进行模拟。圆柱绕流是钝体绕流中的经典问题,可在大量文献中获得实验及数值结果。图4给出了基于上述算法得到的定常、非定常状态下的局部流线图,圆圈为圆柱边界。定常状态下2个反向旋转的Fopple涡对称的附着于圆柱尾部;随着Re增大,Fopple涡交替脱落并向下游运动,流动呈现非定常特征。

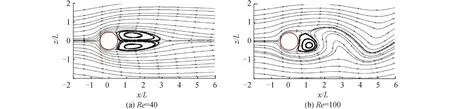
图4 圆柱绕流局部流线图

由表1所示,本文得到的结果与文献结果吻合较好,当前数值方法和程序是有效、可靠的,且离散方案能够保证计算精度。通过修改Lagrange点集的分布函数即可实现对薄平板的绕流问题的求解。

表1 圆柱绕流Re=20, 40, 100阻力系数、斯特罗哈数计算结果

2 雷诺数对平板绕流的影响

图1所示的平板绕流问题,雷诺数被定义为Re=U∞L/ν。本文的模拟中,100≤Re≤1 200。随着Re的进一步增加,考察绕流结构的平均积分参数,如:阻力系数、斯特罗哈数,参数对Re的变化并不敏感[9]。本文在近壁尾流区(x/L<20)对尾流的2次失稳跃迁机理开展了分析与研究。

模型的边界条件为:

入口(x=-11L):均匀来流,u=U∞;w=0。

出口(x=31L):自由出流,∂(u,w,p)/∂x=0。

上、下边界(z=11L,z=-11L):对称边界,∂(u,p)/∂z=0;w=0。

2.1 雷诺数对平板尾流的影响

本文通过模拟得出,对于均匀来流条件下的平板绕流系统,由定常转变为非定常状态的临界雷诺数11015,漩涡由P模式向具有更大的空间尺度的P+S模式转变。二次涡街尚未充分发展的流向范围内(如Re=400, 1420),可以明显观察到以2S漩涡模式为主的尾流结构;该区域内频繁的出现失配单涡,这些失配单涡具有不规则的运动轨迹与空间分布特征。此外,尾流区出现一次跃迁、二次跃迁的流向位置具有时变特征;随着Re的增大,出现跃迁的流向位置向上游移动。

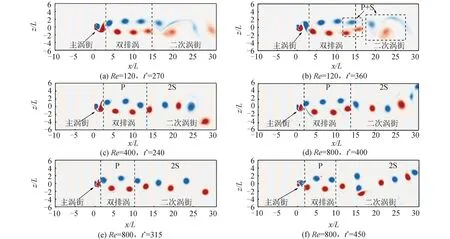
图5 瞬时涡量云图

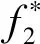
图6 监测点u(t*)功率谱密度函数

2.2 雷诺数对平板阻力的影响

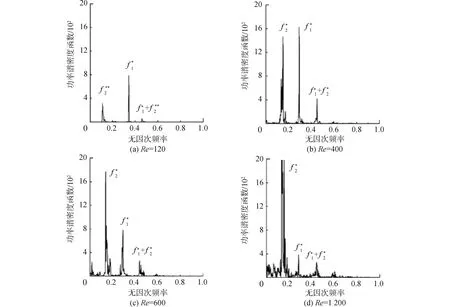
图7 平板阻力系数功率谱密度

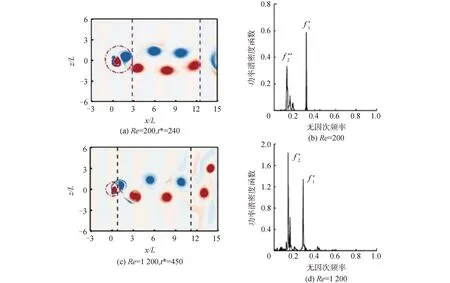
图8 瞬时局部涡量场与监测点p0(2L,0)功率谱密度

3 来流剪切参数对平板绕流的影响

剪切来流条件下,平板绕流问题的边界条件:

入口(x=-11L):速度剪切来流,线性剪切段u(z)=Uc+Gz,G为剪切梯度。

边界x=31L,z=11L,z=-11L处的边界条件同上。

定义剪切参数β=GL/Uc,本节中,0<β<0.166 7;此外,Re=UcL/ν。

3.1 来流剪切参数对平板尾流的影响

图9给出了平板尾流涡脱频率St随剪切参数β的变化规律。Re=100时,均匀来流条件下的平板绕流系统处于定常状态,而在剪切来流的作用下,尾流出现流动分离现象,系统进入非定常状态。值得注意的是,剪切来流对尾涡脱落频率具有一定的抑制作用,特别是在0.06<β<0.12范围内。

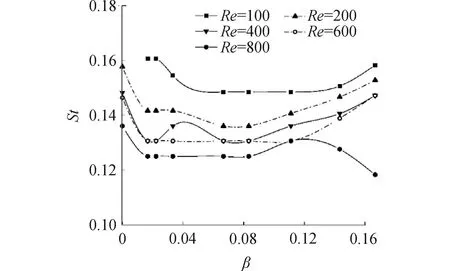
图9 平板绕流系统St随β变化规律

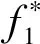
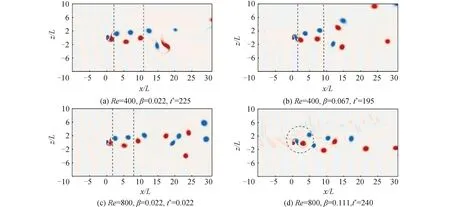
图10 平板绕流瞬时涡量云图

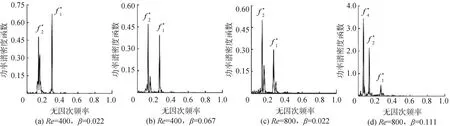
图11 p0(2L,0)点流速功率谱

3.2 来流剪切参数对平板阻力的影响

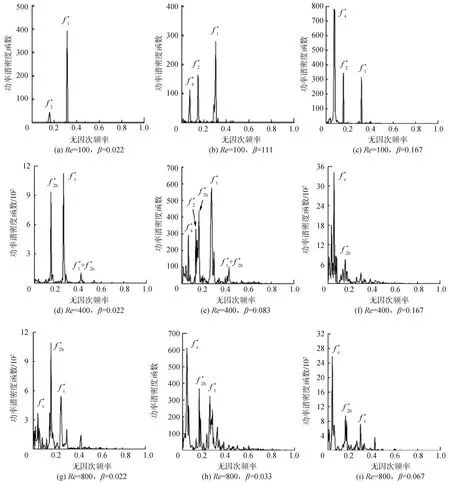
图12 平板阻力系数功率谱密度

本文采用C-C法对Cd(t*)时间序列进行相空间重构并由小数据量法计算最大Lyapunov指数[33-34],用以对平板Cd(t*)的混沌特性进行识别,并据此对Cd(t*)的混沌程度进行定量描述。如图13,本文预测Re=200,阻力系数Cd(t*)转变为混沌特征时间序列的临界剪切参数βc≈0.16。Re=400, 600, 800对应的临界剪切参数分别为βc=0.14, 0.10, 0.03。Re越大,对应的的临界剪切参数越小。在工程实践中,减小雷诺数或来流剪切梯度均可起到抑制平板流向载荷向混沌特征转变的作用。

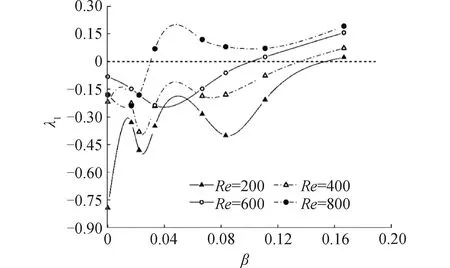
图13 平板阻力系数的最大Lyapunov指数λ1随来流剪切参数β的变化

4 结论

1)雷诺数Re与来流剪切梯度β对垂直平板尾流涡街的影响体现为:对尾流区两次失稳跃迁的流向位置以及对主涡街、双排涡、二次涡街演化过程的影响。

2)在主涡街与双排涡内,漩涡运动轨迹是确定的,流动是周期性的。二次跃迁伴随着漩涡失配-重组现象以及漩涡模式由P模式向大尺度的P+S或2S模式的转变。二次涡街充分发展的区域,大尺度涡结构以及失配单涡的运动轨迹均是不规则的,引发流场的低频、非周期性振荡。

3)Re或β的增大均可导致尾流区一次跃迁与二次跃迁的流向位置向上游移动。

5)剪切来流与平板尾涡结构相互作用,诱发了多频特征的流向载荷。随着来流剪切参数的增大,双排涡结构逐渐失稳甚至消失,平板近尾流受大尺度低频结构主导,阻力系数Cd(t*)具有低频、混沌的特征。在工程实践中,减小雷诺数或来流剪切梯度均可起到抑制平板流向载荷向混沌特征转变的作用。

上述研究结果可为流体机械叶片设计、平板结构减阻、平板结构尾迹控制等问题的理论分析与工程应用提供理论支撑。