叶片破损对压气机性能的影响

2024-05-28王忠义赵佳张晶王萌

哈尔滨工程大学学报 2024年4期

王忠义, 赵佳, 张晶, 王萌

(1.哈尔滨工程大学动力与能源工程学院,黑龙江哈尔滨 150001; 2.中船黄埔文冲船舶有限公司,广东广州 510715)

压气机是影响航空发动机性能的关键部件之一,其气动力特性会受到叶片的几何形状影响[1]。若叶片存在加工误差、发生腐蚀磨损或者受到外物冲击损伤均会产生几何缺陷,从而影响压气机的性能。压气机叶片加工误差不可避免,在一定程度上影响了压气机的气动性能[2-4]。耿少娟等[5]以1.5级压气机为对象,通过测量叶片叶型数据得到加工误差分布特征,采用三维数值模拟方法在设计流量点研究了轮廓度误差对压气机转子和级性能的影响。研究发现叶片加工误差对压气机堵塞流量、全流量范围内的压比和效率均有影响。郭正涛等[6]采用人工神经网络预测了加工误差对叶栅气动性能和角区气动稳定性的影响并发现了加工误差的影响与所处的工况有关,与设计工况相比,近失速工况下气动稳定性对于加工误差更加敏感,并且前缘和吸力面型线的加工误差对损失影响较大。叶片在高压、高速和潮湿空气的冲刷下会发生腐蚀磨损,导致叶片表面粗糙度、叶型发生改变,进而使得流量、压比效率等发生变化[7-9]。卢明亮[10]使用改变叶型尺寸的方法通过数值模拟方法发现叶片腐蚀后的压气机性能出现了一定程度的衰退。李冬[11]得出腐蚀后叶顶间隙变化对效率的影响更为明显,且压气机性能衰退中效率衰退最为严重、流量次之、压比最小。对于航空发动机叶片来说,硬物冲击造成的几何损伤不可恢复。压气机叶片前缘不仅最易冲击受损,同时也是影响气动性能的较为敏感因素,会对内部冲击结构、边界层发展和叶型损失产生显著影响[12-14]。赖安卿[15]通过数值仿真方法发现前缘损伤会导致叶尖区域激波后移,叶中区域分离涡损失增大,从而效率降低,同时减小压力面静压,导致压气机的压比下降。Li[16]以前缘尖端弯曲的叶片为研究对象,进一步了解了轴流压气机旋转失速时的流动特性以及叶片损伤对喘振裕度的影响。吴娜[17]通过数值仿真计算了硬物损伤出现在叶片前缘和顶端时对气动性能的影响,发现损伤缺口(形状为r=5d,深度小于4 mm)在前缘叶尖时进出口总压比几乎没有变化,进出口总压比会随缺口深度增加而明显减小。

本文以跨音速压气机转子对研究对象,采用数值仿真方法探究叶片破损对压气机性能的影响,并针对叶片破损前后压气机的内部流场改变进行对比分析。

1 物理模型及仿真方法

1.1 模型结构与方法验证

NASA rotor 37作为典型跨音速压气机转子被广泛应用到叶轮机械领域 CFD 代码的测试中,本文以此为原模型进行仿真计算,其叶片数目为36,设计转速17 188 r/min,设计压比2.106,设计流量20.19 kg/s[18],更多参数与实验结果可参考文献[19]。

本文选择Numeca软件中的Autogrid5模块进行网格划分,如图1所示,对近壁面网格进行局部加密,保证第1层网格y+<5以适用于所选湍流模型。数值仿真采用 Numeca软件中的FineTurbo模块进行单通道定常计算,假定工质为理想可压缩气体,湍流模型设置为Spalart-Allmaras模型,进口边界条件给定总温 288 K,总压101.325 kPa,进气方向为轴向;出口边界给定平均出口静压,通过逐步增大平均出口静压的方式来计算得到压气机特性曲线;叶片表面和固壁均采用无滑移边界条件和绝热壁面条件。

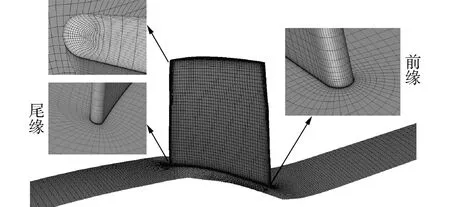
图1 rotor 37网格示意

为了综合考虑计算效率和精度,对网格数量进行了无关性验证。网格数分别为:网格1(25万)、网格2(65万)、网格3(105万)、网格4(140万)。由图2中的不同网格数下压气机特性曲线对比可知,100%设计转速下,105万网格可以达到计算要求,并再将峰值效率工况点和近失速工况点的模拟值与实验值进行对比,发现误差均不超过3.5%,见表1,因此本网格的计算结果具有一定的可信度。

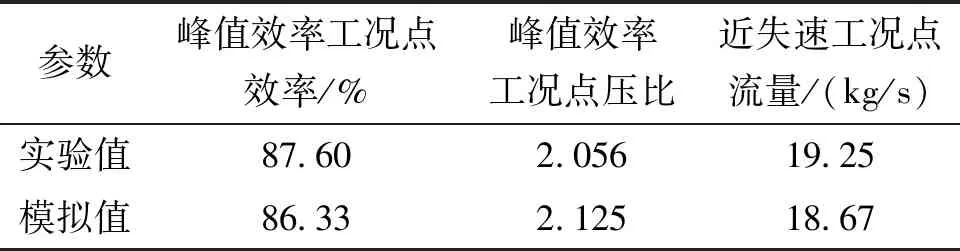
表1 rotor 37实验值与本文数值模拟值

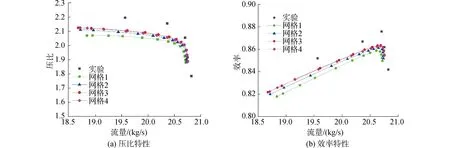
图2 压气机特性曲线对比

为进一步验证数值仿真结果,图3给出了峰值效率工况点出口总压比和总温比随展向高度变化的规律曲线,发现两者变化趋势吻合,虽然仿真值相比实验值存在一定偏差,但误差在合理范围内。图4给出了仿真与实验结果的95%叶高处马赫数对比图,可以看出无论是在峰值效率工况还是近失速工况,压气机内部流场变化一致且数值结果接近,激波发生位置与泄漏流的流向吻合度较高。

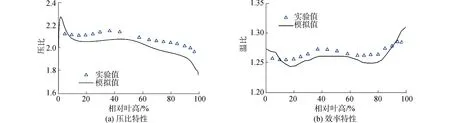
图3 数值模拟与实验的压比和效率特性

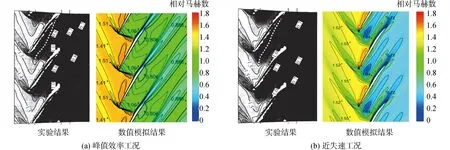
图4 95%叶高相对马赫数云图

综上所述,可以在此原模型的基础上,进行后续研究工作。

1.2 破损叶片模型处理

经对外物损伤的特征分析发现,叶片进、排气边上部多出现小尺度的缺口损伤,进气边叶尖区域常出现大尺度缺口损伤[20]。本文类比某型航空发动机转子叶片实际破损情况[21],简化破损模型为图5所示,是将rotor 37原型在叶顶前缘位置进行宽度和高度均为7.5 mm的三角形缺口破损,通过数值仿真方法来考察叶片破损对压气机性能和内部流场的影响。

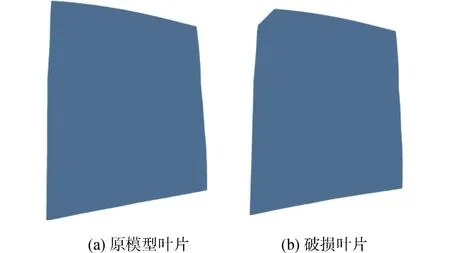
图5 叶片原型与破损模型几何结构

2 破损叶片仿真结果及分析

2.1 总体性能分析

基于流量可将压气机的稳定裕度SM为:

SM=(mDEmNS/mDE)×100%

(1)

式中:mNS、mDE分别为压气机近失速工况点和设计工况点的质量流量。

压气机设计工况点流量为20.19 kg/s,根据计算结果可知叶片破损前后的近失速流量分别为18.67 kg/s和19.05 kg/s,代入式(1)可知叶片破损后压气机稳定裕度由7.53%降至5.65%,下降了25.0%。图6为压气机叶片破损前后的工作特性曲线对比,叶片发生破损使得工作特性曲线下移,工流量范围缩短,压气机各工况点的总压比和绝热效率都呈现降低趋势。由计算结果可知,叶片破损后峰值效率工况点压比由2.005 6降低为1.992 3,下降了0.663 1%;效率由86.33%下降为85.65%,下降了0.787 7%。近失速点流量由18.67 kg/s上升为19.30 kg/s,提高了3.333 5%;堵塞点流量由20.76 kg/s降低为20.64 kg/s,下降了0.58%。结合以上数据和图6可知,叶片破损导致了压气机气动性能衰退,其中对稳定裕度的影响更对显著。

图6 破损后压气机特性曲线

2.2 内部流场分析

图7给出了100%设计转速、2个典型工况下,叶片原型和破损模型的出口总压比沿叶高分布曲线。可以看出峰值效率工况和近失速工况下,叶片破损后在全叶高范围内的出口压比均呈降低趋势,最大衰退值可达0.097,且这种降低的趋势由叶顶向叶根延伸且程度减弱,这表明破损模型对压气机性能造成衰退的影响主要集中在叶顶部分。根据破损位置及形状,可首先推断出叶顶压比降低的原因之一是由于叶顶弦长减小导致对气流的做功能力减弱,而其他更深层次的原因需后续对叶顶流场进行详细分析。

图7 转子出口总压比沿叶高分布曲线

图8给出了破损模型在峰值效率工况点和近失速工况的子午面密流分布,其中密流Density-V定义为轴向速度与密度的乘积,反映了压气机的通流能力,其数值降低幅度较大处即为失速最易发生的位置。结合图8(a)和(b)可知,从峰值效率工况到近失速工况,叶顶位置的密流下降最多,可以判定失速会首先在叶顶发生;同理,叶片破损对稳定裕度的影响也主要是由于对叶顶流场结构产生了更为明显的改变。

图8 子午面密流分布

图9给出了100%设计转速时,2典型工况下的98%叶高马赫数分布。叶片在2个工况点下于破损位置处都产生了高马赫数区,且叶片的附面层厚度都有所增加,通道内产生的堵塞区域和后部尾迹区域范围均变大,致使流动损失的增加,从而造成了压气机效率的降低。对比破损前后的近失速工况图,可知破损模型的吸力面侧激波位置较原型发生了前移且激波强度增大,导致附面层提前分离,压力面的低马赫数流动区域也明显增大。由于进口处的激波位置越靠前,激波强度越大,压气机的流动稳定性越差,所以叶片破损使得压气机的稳定裕度减小。

图9 98%叶高相对马赫数云图

图10给出了转子叶片在98%叶高处叶片表面静压系数分布曲线,吸力面与压力面的静压差可以反映叶型的负荷情况。对峰值效率工况分析可知,前30%弦长范围内,破损使得叶片的静压系数有所下降,且吸力面下降更为严重,表明破损位置附近的叶片静压差增大,负荷增大,泄漏流增强;后30%弦长范围内,叶片的负荷受到破损的影响较小。对近失速工况分析可知,压力面的静压系数基本未受破损影响,而吸力面在前25%弦长范围内的静压系数明显下降。再综合分析2个工况下吸力面的压力阶跃位置可知,破损叶片导致了吸力面的压力阶跃提前,即激波位置向前缘移动。由此可见,叶片破损对吸力面侧流场产生的影响比压力面侧更深。

图10 静压系数沿弦长分布

针对吸力面侧流场展开分析,图11给出了叶片破损前后的吸力面极限流线图。在峰值效率工况下,破损模型的顶部区域流线不再平行于上端壁面且流动不均,出现了径向流动(图中A区),同时叶顶尾部的流线也受到了一定影响;附面层分离线的起始位置上移(图中标号a处),分离线后的流线弯曲曲率变大,分离涡强度有所增加,可以分析出破损模型的气流流动损失较大,这也是其最高效率数值低于原模型的原因之一。在近失速工况下,叶尖破损产生的涡分布进一步加大,对叶顶尾部流动的影响加深;可明显看出叶片上部的分离线产生扭曲,叶顶和60%～80%叶高的分离点位置(图中C区)都有一定程度上的向后移动,其中顶部的分离点位置后移最严重。虽然叶顶激波位置向尾缘移动降低了激波附面层分离损失,但线后附面层内低能流体的回流堆积在了叶顶(图中B区),其与主流汇聚后被带走,加大了流动阻塞和流动损失。

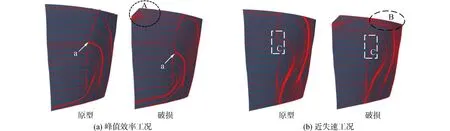
图11 吸力面极限流线分布

在跨声速压气机中,其损失和工作稳定性主要受叶顶泄漏流以及泄漏涡与激波的相互作用所影响。图12给出了转子叶片原型和破损模型的叶顶泄漏流流线分布。可见,破损处由于叶顶间隙加大导致叶顶泄漏涡范围增加,且泄漏流向下游流动过程中,速度逐渐降低,打到相邻叶片压力面后发生二次泄漏也加剧。在峰值效率工况,原模型和破损模型的叶尖前缘泄漏流与主流作用生成的泄漏涡强度都比较低,对压气机的稳定性没有显著性影响;而在近失速工况,分析2个模型的叶顶流线可知,通道激波的阻滞作用将泄漏涡破碎,叶尖前半部分的压力面附近形成了大面积低速区域;叶尖吸力面后半部分因激波导致的强逆压梯度使附面层进行分离,之间的相互作用将流道堵塞,造成压气机失速。相对于原模型,破损模型由于叶尖前缘发生损伤而产生了十分强烈的激波,激波会导致前缘存在低速回流区,但由于破损后叶顶前半部分间隙有所增加,泄漏流会变得更强,可将吸力面侧的低能流体团吹走,但泄漏流在叶顶位置处引入了泄漏涡,使附近位置流动变得复杂化。

图12 叶顶泄漏流流线分布

图13给出了近失速工况下叶片破损前后的子午面相对总压分布,可发现叶顶位置都存在着由泄漏涡(见图12(b))造成的大范围低相对总压区,该区域从叶片前缘处起,逐渐沿如前所述的泄漏涡轨迹向通道下游发展。由于叶片破损导致叶顶泄漏涡强度加大,所以其顶部破损位置处产生了很大的低压区,进一步说明了叶顶破损导致流场恶化且总压损失十分严重。

图13 子午面相对总压分布

对最高效率点进行分析,图14给出了叶片破损前后不同流向截面叶顶位置处的熵值分布云图,发现原模型和破损模型在叶顶区域的熵值均较大。经对比发现,破损模型在95%叶高以上的破损位置更是出现了局部高熵区,靠近尾缘区域也存在较大面积的高熵区,其位置主要对应着附面层的分离区和叶片的尾迹区,由此可知叶片破损后存在着分离损失、尾迹损失和掺混损失较多;同时,压气机内部的熵增也会造成温比的上升,进而降低了压气机整体的效率。