钛合金室温受压蠕变损伤本构模型

2024-05-28郭育豪刘刚宋育泽

哈尔滨工程大学学报 2024年4期

郭育豪, 刘刚,2, 宋育泽

(1.大连理工大学船舶工程学院,辽宁大连 116024; 2.大连理工大学工业装备结构分析优化与CAE软件全国重点实验室,辽宁大连 116024)

钛合金具有密度低、比强度高、耐腐蚀、低磁性以及高透声系数等特性[1],被广泛用作深潜器耐压壳的主要材料。目前国内外作业型载人深潜器的工作作业时间主要集中在4～12 h,下潜深度为4 500～7 000 m[2]。随着深海科学研究和深海资源开发等领域的发展,对耐压壳的作业时间和下潜深度的要求不断提高。早在20世纪70年代,Odegard等[3-4]发现TC4材料在室温下的存在明显的蠕变现象。钛合金耐压壳在深海高压环境下发生不可逆的蠕变变形,尤其是开口、过渡等结构局部几何不连续区域。因此,研究钛合金室温高压环境下的蠕变行为很有必要。

连续损伤力学(continuous damage mechanics,CDM)是一种基于连续介质假设来研究材料在外部载荷作用下逐渐劣化直至失效的方法,通过在本构方程中引入损伤变量来度量材料的劣化程度,基于实验或者微观力学建立损伤演化方程演示累积[5]。自从Kachanov[7-8]引入“连续度”的概念描述蠕变损伤对材料的劣化影响[6],CDM已经成为研究蠕变破坏的主流方法之一。

深潜器在服役期间受到超高静水压力作用,绝大多数区域的应力处于受压状态,目前已有的高温情况下蠕变损伤评估方法主要针对拉伸载荷,并且所采用的模型根据单轴拉伸蠕变实验得到。而实际上大部分材料拉伸和压缩所表现出来的蠕变行为不一致[9]。因此,对于耐压壳这类绝大部分区域处于压缩应力状态的结构,拉伸蠕变本构模型的计算结果过于保守。另外,目前已有的蠕变损伤本构模型主要针对高温情况,还没有基于连续损伤力学理论提出相应的室温蠕变损伤本构模型。为了准确地计算深海结构的蠕变损伤响应,有必要建立适用于受压情况下的室温蠕变损伤本构模型。

本文首先根据钛合金材料室温蠕变的特点,基于微分自洽法提出了钛合金材料室温蠕变损伤本构模型,并基于现有实验数据对压缩载荷作用下的参数进行拟合。通过V型缺口板数值模拟,并对环肋耐压壳进行了分析,验证本文所提出模型的工程适用性。

1 蠕变损伤本构模型

常温下蠕变应变主要是由于位错累积运动和微孔洞造成,微孔洞通常在晶界上产生[10]。本文基于以下假设推导与损伤耦合的蠕变本构方程[11]:

1)加载方式为比例加载,在整个蠕变过程中主应力方向不变;

2) 微孔洞只会出现在法线与第1主应力方向相同的平面;

3) 与整体应力水平相比,孔洞面上的法向应力为一小量,即忽略微裂纹表面的拉应力;

4) 忽略微裂纹之间的相互影响;

5) 材料的蠕变行为服从Norton律。

(1)

在没有微裂纹的情况下,总应力势能函数为[11]:

(2)

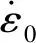
在无限大的材料内存在一外法线x2,与远场的第1主应力σ1方向相同,且d为币状微裂纹直径,如图1所示。

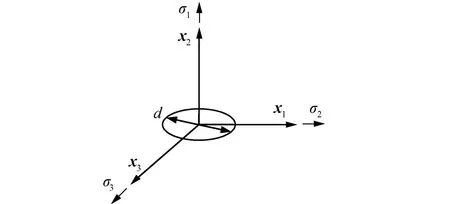
图1 币状裂纹模型

单个微裂纹对整体应力势能函数的贡献为[11]:

(3)

忽略微裂纹直接的相互影响作用,N个间距较大的币状微裂纹材料的总体势函数为:

Φ=Φ0+NΦ1

(4)

外力作用下,蠕变首先出现在最容易发生滑移的晶粒处,之后载荷会重分配到附近稳定性较差的晶粒。晶粒的滑移有限,因此蠕变应变率逐渐降低。TC4钛合金α+β双相钛合金,在不同相的边界上存在诸如内部屏障、内势垒等的蠕变阻力,在室温环境下没有足够的能量突破阻力[12-14],在宏观上表现为蠕变应变率不断减小甚至接近0,这种现象在压缩载荷下更加明显。考虑到这种位错堆积的现象与时间有关,在室温下势函数为:

Φ=Φ0+f(t)NΦ1

(5)

式中f(t)=αt为与时间相关的函数。同时蠕变第1阶段的位错堆积程度小,因此可以认为其对室温蠕变的影响主要在第2阶段。若假设稳态阶段蠕变应变与时间成线性关系,考虑位错堆积对蠕变应变的影响也主要体现在稳态蠕变阶段:

f(t)=αt

(6)

式中α为引入的材料参数,与应力有关,势函数Φ为:

(7)

式中ρ为微裂纹密度,可以表示为:

(8)

将式(7)代入式(1),蠕变应变率张量为:

(9)

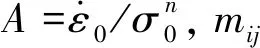
单轴应力状态下式(9)退化为[15]:

(10)

对微裂纹密度ρ微分可得:

(11)

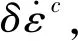
(12)

(13)

将其推广到三维形式:

(14)

考虑蠕变第1阶段[7],采用时间硬化模型,则式(14)变为:

(15)

包含币状微裂纹的圆柱形晶胞模型如图2所示,晶胞直径和高度为D。

图2 含币状微裂纹晶胞模型示意

使用微裂纹面积与晶胞截面积的比值表示损伤:

(16)

单位体积内微裂纹的数量为:

(17)

则微裂纹密度可以用损伤表示为:

(18)

将式(18)代入式(15)中,最终得到与损伤耦合的蠕变本构方程:

(19)

从式(19)可以看出,当α<0时,蠕变应变率随着时间推移逐渐衰减至0。

当损伤为零时,式(19)退化为:

(20)

退化结果与经典的时间硬化模型一致。

损伤演化方程是蠕变损伤模型中另一个重要的组成部分,其中常用于数值计算的是基于应变的损伤演化方程。

该模型是基于延性耗竭理论提出的,该理论将产生蠕变损伤处的微元等效为一系列单轴试样,当局部微元累积的蠕变应变达到阈值后完全损伤[16]。损伤累积模型为:

(21)

使用多轴蠕变延性因子EMCDF建立单轴蠕变断裂应变和多轴蠕变断裂应变之间的关系。目前已经提出了多种多轴蠕变延性因子模型,但具体哪一种最优尚无定论。目前主流的模型为[7,17-20]:

(22)

(23)

(24)

EMCDF=2(1-3σm/σeq)

(25)

(26)

综合比较几个典型的多轴延性因子,式(26)模型更适合有限元计算,并且具有明确的物理意义,因此本文选择该模型作为多轴蠕变延性因子。

2 蠕变损伤本构模型参数拟合

王雷等[21]对室温环境下TC4ELI材料进行了压缩蠕变试验,使用其试验数据拟合本文所提出本构模型的参数。在材料蠕变的初始阶段,损伤很小,式(19)可简化为式(20)时间硬化率模型。因此,A、m、n可以通过蠕变初始阶段的单轴试验数据拟合得到。为便于拟合,对式(20)进行积分,同时考虑初始蠕变应变为0,将其化为蠕变应变的方程为:

(27)

基于4种应力水平(0.8RPC0.2,0.85RPC0.2,0.9RPC0.2,1.1RPC0.2)下的蠕变曲线初始段,全局拟合得到参数A、m、n的值,如图3所示。拟合得到A为1.287 7×10-13MPa-nh-m,m为-0.632 3,n为3.162 5。

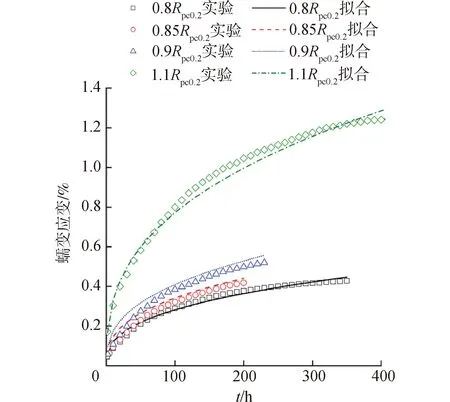
图3 TC4ELI钛合金蠕变第1阶段拟合曲线

通过基于有限元的逆向反法推初步确定对应应力下的α,结果如表1所示。

表1 α的初步确定

绘制如图4所示的α-应力散点图,经观察发现,α与应力之间近似呈线性关系,可以表示为:

(28)

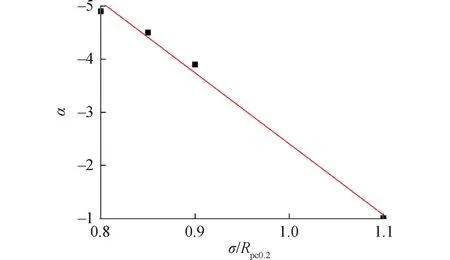
图4 α与应力之间的关系

式中Rpc0.2为规定非比例压缩强度,对于TC4ELI材料而言为992.5 MPa。线性拟合得到α1为13.37 h-1,α2为-15.78 h-1。

根据上述确定的参数,拟合得到图5所示室温环境下TC4ELI的压缩蠕变曲线。相对误差情况如图6所示,可以发现,除去初始阶段因为蠕变应变较小而造成相对误差过大外,拟合结果与试验结果之间的相对误差S范围为-10%≤S≤10%,说明本文所提出的蠕变损伤本构模型可以很好地描述室温环境下钛合金的压缩蠕变行为。

图6 TC4ELI蠕变应变误差分析

3 蠕变损伤数值模拟与讨论

本文基于蠕变损伤本构关系和蠕变损伤演化方程,建立了结构损伤演化速率和蠕变应变场之间对应关系,并通过有限元软件ABAQUS计算受压结构的损伤演化累积过程。由于材料损伤劣化引起单元刚度阵衰减等问题,具有较强的非线性。通过选择合适的结构刚度阵迭代方法和适度的步长,保证蠕变过程在非线性有限元计算过程中的收敛性。使用USDFLD和CREEP子程序,将以上损伤本构关系与损伤演化方程编入计算模块,实现在蠕变载荷下结构各单元损伤累积过程,同时实现随着损伤演化,材料性能不断劣化的过程。

室温受压蠕变损伤本构模型如式(19)、(21)、(26)所示,相关参数如表2所示。

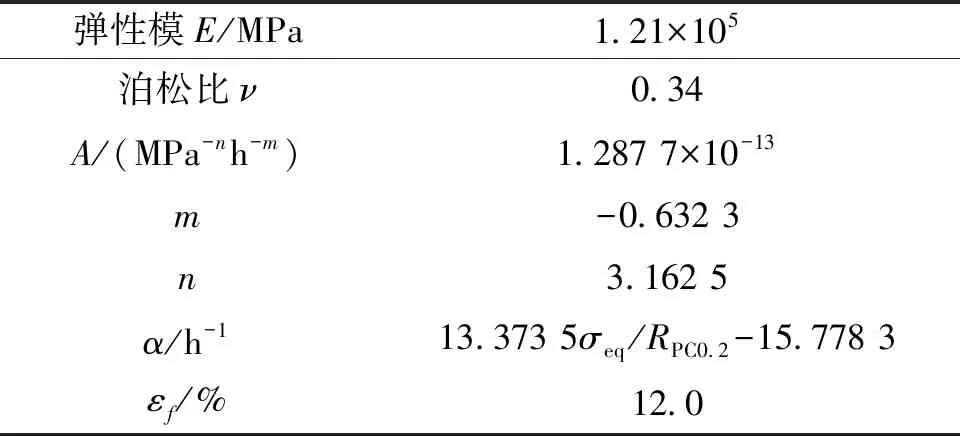
表2 受压模型材料参数

进行对比时所选取的室温受拉蠕变应变本构模型为[23]:

(29)

其中:

(30)

损伤演化模型仍然基于延性耗竭理论,多轴延性因子采用不需要额外参数的Manjoine模型[20],如式(25)所示。

3.1 含V型缺口平板受压蠕变模拟

以85 mm×50 mm的含V型缺口平板为例[24],说明采用拉伸模型与本文所提出的压缩模型的不同,如图7所示。右侧受到150 MPa的压力,左侧刚固,加载300 h。缺口附近存在应力集中,改处为蠕变应变和蠕变损伤累积的主要区域,重点分析虚线框内的区域。该区域网格尺寸为0.2 mm,采用四节点平面应力单元。

图7 含V型缺口平板受压模型

采用拉伸蠕变损伤本构模型和压缩蠕变损伤本构模型计算得到的等效应力云图、等效蠕变应变云图以及损伤云图分别如图8～10所示。应力集中处的数值如表3所示,使用根据拉伸蠕变实验得到的相关蠕变损伤本构模型来模拟受压结构会导致计算结果过于保守,其中等效蠕变应变的相对误差高达168.20%。

表3 拉伸、压缩模型数值结果对比

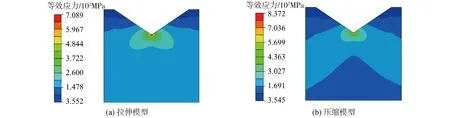
图8 加载300 h等效应力云图

图9 加载300 h等效蠕变应变云图

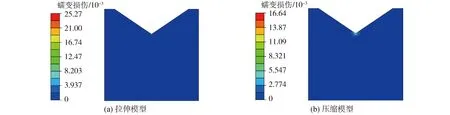
图10 加载300 h损伤云图

图11为应力集中处等效应力、等效蠕变应变以及损伤随时间的变化曲线,从图11可以看出,在初始时刻蠕变应变速率很大,一方面是因为模型中蠕变第1阶段初始时刻的蠕变应变速率最大;另一方面是因为初始时刻应力水平很高。随着时间增加,蠕变应变速率不断减少并趋于平稳,并未发生破坏,这是因为室温蠕变不存在第3阶段,不会出现失稳现象。根据延性耗竭理论,蠕变损伤的演化也呈现相同的趋势,损伤达到一定值后就基本不增加或增加速率很小。同时,因为蠕变应变以及损伤的联合作用,应力发生重分配,缺口处应力迅速降低,并且因为损伤最终趋于稳定,裂尖处的单元仍具有较大的承载能力,应力最后并不会衰减至0,而是趋于稳定。

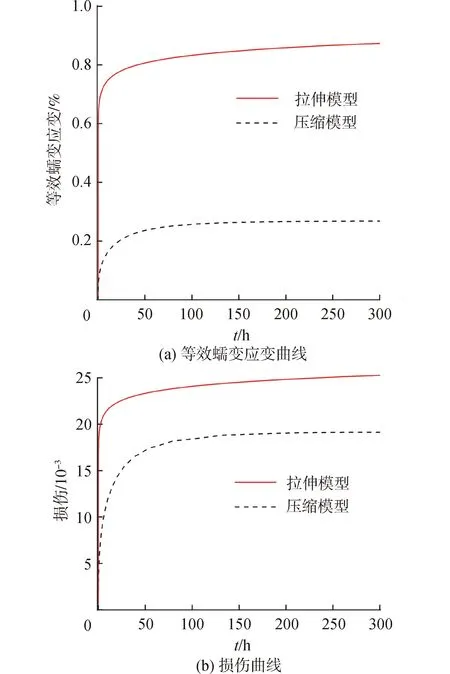
图11 算例1应力集中处物理量变化情况

除此之外,通过对比不同模型的计算结果也可以发现,根据拉伸蠕变实验得到的相关蠕变损伤本构模型会过分地高估等效蠕变应变、蠕变损伤以及等效应力的演化情况。

3.2 环肋耐压壳受压蠕变模拟

以环肋耐压壳结构为例,说明本文所提出模型的工程适用性。几何模型如图12所示,该结构长L为2 148 mm,半径R为550 mm,板厚k为14 mm,环肋T型材尺寸为81 mm×40 mm×8 mm×14 mm。作业深度为4 km,外部压强P为40 MPa。考虑其对称性,建立1/8有限元模型,相应对称面上节点施加对称边界条件。局部有限元网格如图13所示,网格尺寸为4 mm,总单元数为341 220。

图12 耐压壳结构

图13 1/8模型网格示意

首先进行静力分析,得到的等效应力云图应力如图14所示,内壳环肋处应力水平最高,该处在外部静水压力作用下处于受压的应力状态。首部球形壳处应力水平较低,根据式(19)可知,应力水平较低的区域蠕变应变率以及损伤演化速率都较慢,因此,对计算模型进行简化以提升计算效率,将首部球形壳等效为均布压力:

(31)

图14 1/8模型等效应力云图

计算得到的等效应力云图如图15所示,应力集中处结果如表4所示。从表中可以看出,以1/8模型的计算结果作为参考值,2种模型应力集中处的计算结果误差仅为1.98%,而单元数减少了将近1/2,因此后续采用简化模型进行蠕变损伤的相关分析。

表4 2种模型结果对比

图15 简化模型等效应力云图

保持外部压强为40 MPa,300 h后的等效应力云图、等效蠕变应变云图以及损伤云图分别如图16所示。从图中可以看出,因为内壳环肋处等效应力最大,因此该处蠕变应变率也最大,在300 h时,等效蠕变应变达到1.056%。根据延性耗竭理论,该处损伤也最大,在300 h时,损伤达到0.021。

图16 加载300 h后各物理量分布情况

初始应力水平最高处的各物理量演化情况如图17所示。从图中可以看出,因为损伤会导致材料劣化,丧失承载能力,该处的等效应力会逐渐衰减,TC4钛合金α+β双相钛合金,在不同相的边界上存在诸如内部屏障、内势垒等的蠕变阻力,在室温环境下没有足够的能量突破阻力[12-14],蠕变应变率和损伤演化速率会随着时间推移速率逐渐减少。