基于KPCA-GA-BP模型的页岩气集输管道的内腐蚀速率预测

周逸轩,彭星煜,耿月华,王思汗

(1.西南石油大学新能源与材料学院, 南充 637000;2.西南石油大学石油与天然气工程学院, 成都 610500;3.西南石油大学信息学院, 南充 637000;4.中国石油西南油气田分公司安全环保与技术监督研究院,成都 610041)

碳达峰、碳中和是国家重大战略,发挥天然气清洁低碳、高效稳定的独特优势,对于我国碳达峰、碳中和目标的顺利实现具有重要意义[1]。作为一种非常规天然气,页岩气在我国能源结构中占据了重要地位。但目前页岩气集输管道的安全面临较大挑战,特别是腐蚀穿孔引起的泄漏问题[2]。页岩气集输管道由于管径较小、弯头较多,在线检测不具备良好的实现条件[3]。因此,建立一套页岩气集输管道内腐蚀预测模型具有重要的意义。最经典的腐蚀预测模型是DeWaard 和Milliams建立的模型,针对单一的CO2腐蚀预测,该模型具有一定的准确性[4-5]。但页岩气集输管道的腐蚀机理比较复杂,目前一些研究显示,其腐蚀是由SRB与CO2协同产生的,建立简单的显式模型很容易出现欠拟合的现象[6]。因此,隐式模型是更好的选择,其中运用最广泛的是神经网络[7]。反向传播(BP)神经网络具有良好的自学习、自适应和泛化能力[8],并且可以引入一些算法对神经网络进行优化,以实现更准确的预测。例如,遗传算法(GA)和核主成分分析法(KPCA)可以提高预测精度[9-12]。优化后的神经网络预测结果优于单独使用BP神经网络。笔者通过管道漏磁检测器检测和PIPESIM 拟合软件模拟结果获得训练数据,通过这些数据建立BP 神经网络模型,并通过GA 和KPCA 对模型进行优化,采用该模型预测另一条相邻页岩气集输管道的腐蚀速率,并进行现场开挖,以验证模型的准确性,以期为页岩气集输管道的腐蚀速率预测提供一种新的思路。

1 BP神经网络模型的建立

神经网络是一种机器学习技术,是深度学习的基础,也是当前研究的热点。人工神经网络或连接系统是受到生物神经网络模糊启发的计算系统[13]。BP神经网络的建立大致可以分为两个过程。首先,通过前向传播得到预测值:

式中:S j为节点j的加权计算结果;w ij为加权值;x i为节点i的输出值;b j为节点j的阈值。

主动函数选择sigmoid:

式中:x j为节点j的输出值。

通过预测值与实际值的相对误差平方和的最快下降方向调整网络的权值和阈值:

式中:E为损失函数;d j为最终预测值;y j为实际值;η为学习率。

精度检验是衡量模型优劣的重要方法,采用均方误差(MSE)作为预测结果的评价指标,见式(6):

式中:Y i为真实值;^Y i为预测值。

BP神经网络有多种训练方法,不同训练方法对权值的修正过程不同,这会对最终模型产生较大影响[14]。TraingD 和TraingDM 是常用的训练函数,Traingda、 Traing DX、 Traingd、 TrainRP、TrainCGF、TrainCGB、Trainscg、Trainbgf 等是快速训练函数。训练节点形式尤为重要[15],笔者选取隐含层节点为(8,8,1)、(5,5,1)、(8,1)、(5,1)。

针对某页岩气集输管道,绘制了管道纵断面图。该管道起点位于某平台,终点位于某集气站。在平台和集气站获取了该管道运行期间的进出口温度、进出口压力、气质组分等参数,通过积分求得其在管道运行期间的平均值,见式(7):

式中:X为管道运行参数;t0为管道开始运行的时间;t1为调研的时间。

通过上述公式得到的管道出口参数,通过PIPESIM 软件模拟仿真得出管道沿程运行参数,总共获取了165个节点的数据。选取155个点作为训练点,10个点作为验证点。运用高清漏磁检测器检测腐蚀速率,通过测量管道沿线金属实际壁厚,计算出壁厚损失,再根据管道的实际运行时间,求出腐蚀速率,计算的公式见式 (8):

式中:v为腐蚀速率,mm/a;Φ1和Φ0分别为管道实测和管道设计壁厚,mm;Δt为管道运行时间,h。

文献[16]指出,页岩气集输管道的腐蚀由硫酸盐还原菌(SRB)与CO2协同作用,其主要影响因素还有温度、压力、持液率、CO2分压、气体流速、液体流速和管道倾角等,根据PIPESIM 软件模拟结果,各项参数取值范围见表1。

表1 训练参数的取值范围Tab.1 The range of training parameters

将表1中各项参数作为输入层,腐蚀速率作为输出层。学习率为0.001,比较了不同节点类型下不同训练方法的均方误差,如表2所示。

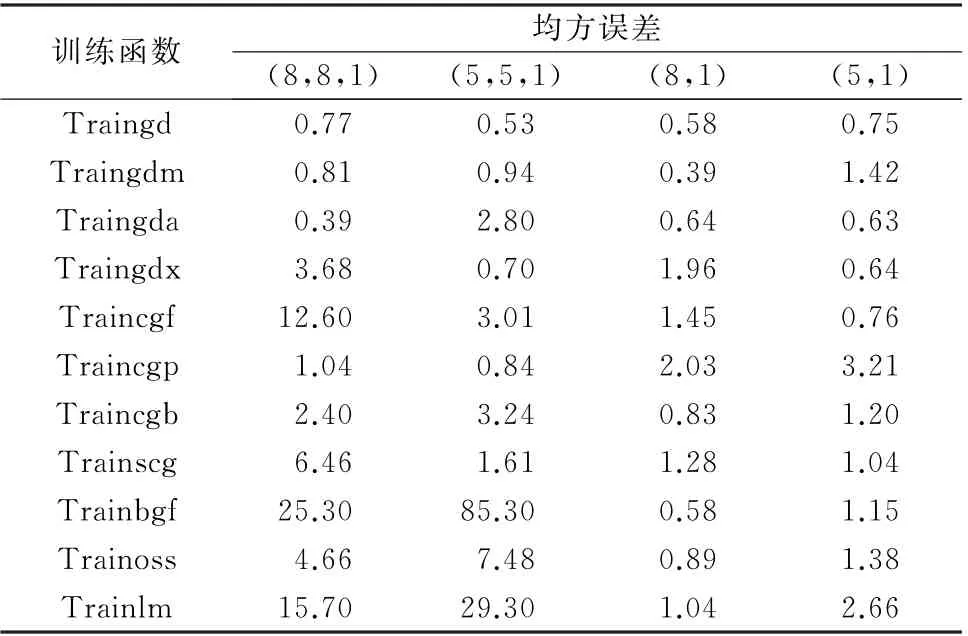
表2 不同训练方法和节点类型条件下的均方误差Tab.2 MSE of different training methods and node types

由表2可以看出,当训练方法采用(8,1)隐含层形式的Traingdm 函数时,均方误差为最小值。后续研究采用该节点和训练方法。利用Traingdm 修正权值的过程如下:

式中:α为动量因子,选择默认值为0.9。

2 基于KPCA与GA对模型的优化

2.1 遗传算法的运用

霍兰德在1960年提出了基于达尔文进化论概念的遗传算法,之后,戈德堡于1988年进一步优化了遗传算法[17]。神经网络权值和阈值初始值的选择会对最终预测结果产生很大影响,因此选择合理的初始值非常重要。研究显示,使用GA 优化BP神经网络的初始权值和阈值是可行的[18-19]。遗传算法将神经网络的权值和阈值作为一个种群,通过适应度函数计算种群中个体的适应度,再通过选择、交叉和变异操作找到具有最佳适应度值的相应个体,最终得到神经网络的最佳初始权值和阈值。

遗传算法中有很多关键参数,其对最终神经网络的表现有很大影响。笔者通过改变进化次数、种群大小、交叉概率和变异概率,研究了其对预测精度的影响。其中,进化数为10、50、200、500和1 000,种群规模为10、25、50、75和100,交叉概率为0.3、0.6和0.9,计算变异概率为0.05、0.10、0.15和0.20。图1～4对比了不同关键参数下腐蚀速率的预测结果与实际结果。

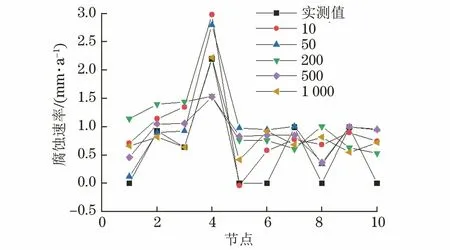
图1 不同种群规模下的腐蚀速率Fig.1 Corrosion rate under different population size conditions

图2 不同进化次数下的腐蚀速率Fig.2 Corrosion rate under different evolution frequency time conditions

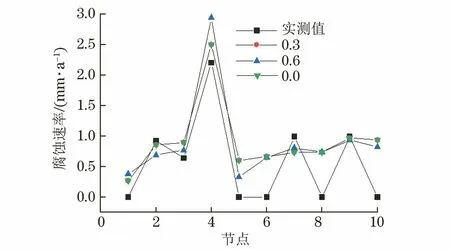
图3 不同交叉概率下的腐蚀速率Fig.3 Corrosion rate under different crossover probability conditions

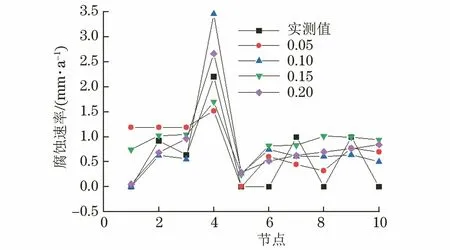
图4 不同变异概率下的腐蚀速率Fig.4 Corrosion rate under different mutation probability conditions

表3显示了选择不同关键参数时的均方误差。在随后的研究中,选择进化的数量为50,种群规模为100,交叉概率为0.3,突变概率为0.2。图5显示了该参数下遗传算法的适应度曲线。此时MSE 最小,为0.21。

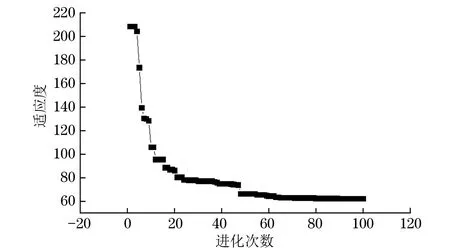
图5 适应度曲线Fig.5 Fitness curve

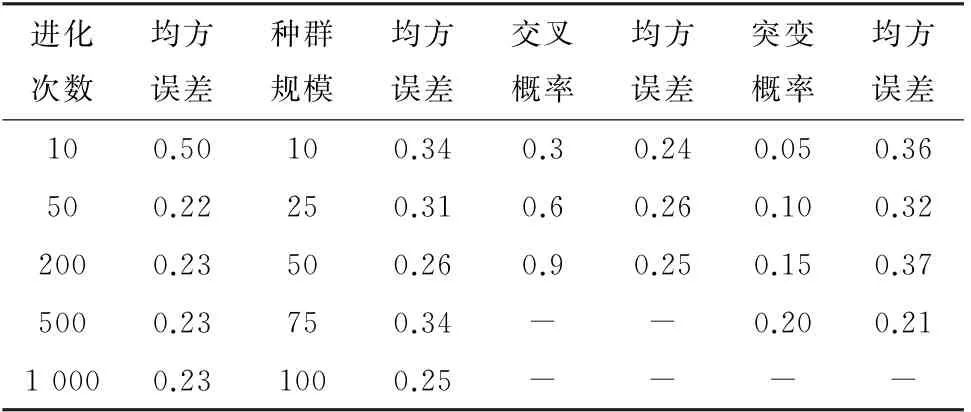
表3 遗传算法不同关键参数选取下的腐蚀速率预测误差Tab.3 MSE of different key parameters of genetic algorithm

2.2 核主成分分析法的运用

前期研究将温度、压力、持液率、CO2分压、液体流速、气体流速、管道倾角等7个维度作为腐蚀影响因素进行分析。相关研究表明,降低维度可以减少噪声数据,提高神经网络的预测精度。因此,提出KPCA 对数据进行降维处理[20]。在多元统计领域,核主成分分析是主成分分析的扩展。使用一个核,KPCA 的初始线性操作在可再现的核希尔伯特空间中进行。

基于MATLAB编程,采用KPCA 对数据进行降维,选取径向基核函数作为核函数。

降维后的结果如表4所示,此时,原有具有物理意义的7个参数转化为不具有物理意义的7 个参数,用X1～X7来表示,且前4个主成分的累计贡献率已达到98%,即X1～X4已经能够包含之前7个具有物理意义的参数的98%的信息,故选取此4个主成分作为管道内腐蚀的影响因素,得到重构后的数据序列。同样,从重建数据中选取155个点代入GA-BP进行训练,选取10个点进行验证。神经网络的损失曲线如图6所示。可以看出,在第96节点时,验证损失达到最小值0.12,之后逐渐增大。因此,选择此时的权值和阈值参数作为最终的建模参数,整个模型的建立流程如图7所示。

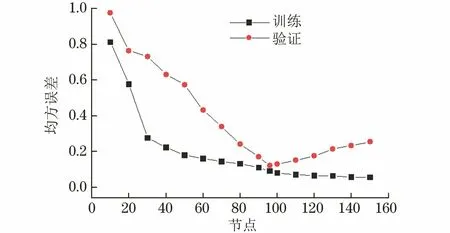
图6 神经网络的损失曲线Fig.6 Loss curve of neural network

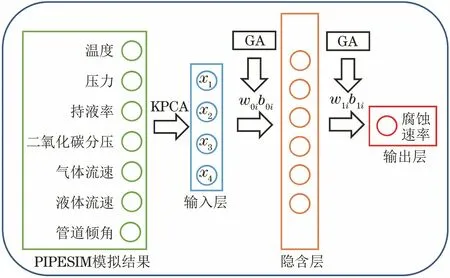
图7 模型的建立过程Fig.7 Establishing process of the model

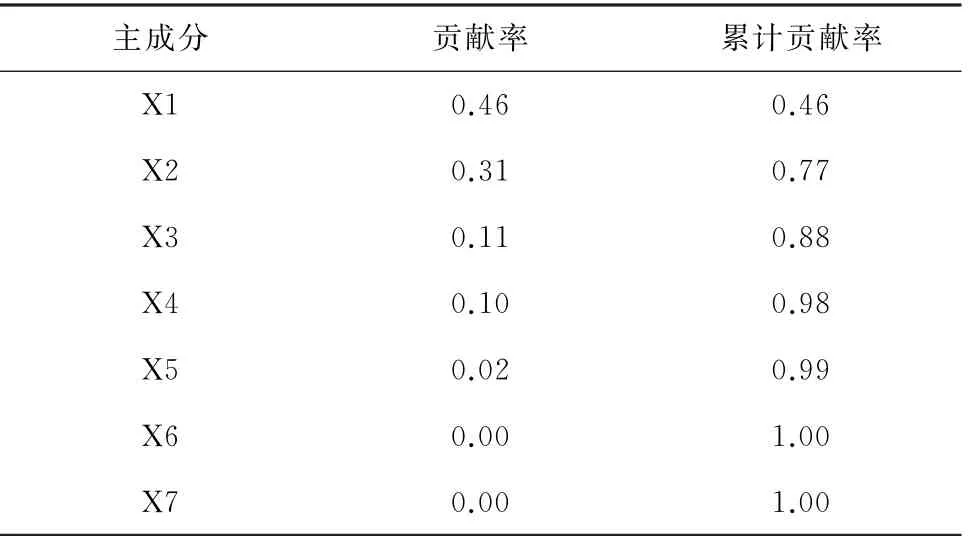
表4 核主成分分析结果Tab.4 Results of KPCA

由图8和9可见:采用KPCA-GA-BP 模型所得腐蚀速率的均方误差显著小于采用GA-BP和BP模型所得结果。因此,采用KPCA-GA-BP 模型预测页岩气集输管道内腐蚀速率可显著降低预测误差,此模型可用于工程实践。

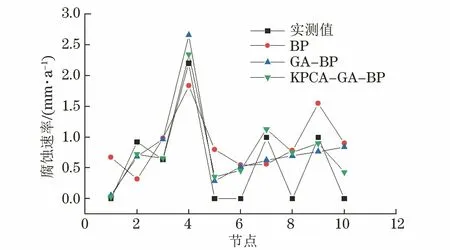
图8 神经网络优化前后的预测值Fig.8 The predicted values before and after neural network optimization

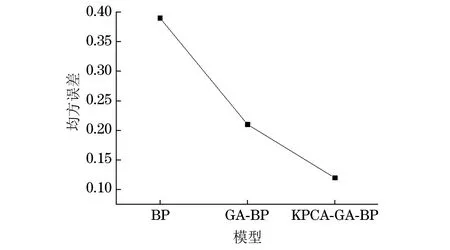
图9 三种模型的预测误差Fig.9 MSE of three models

3 实例验证

运用上述模型,对另一条相邻管道的腐蚀速率进行的预测和验证。与之前用于训练的管道一样,在管道的入口和出口采集到温度、压力、组分等参数,并通过式(7)计算得到平均运行参数,通过PIPESIM 软件进行仿真,求得管道的运行参数,用KPCA-GA-BP模型对管道的腐蚀速率进行了预测。同时在现场选取了10个点进行开挖,测量管道金属实际壁厚,再根据管道的实际运行时间,通过式(8)求出管道的实际腐蚀速率。预测结果与开挖结果对比见图10。

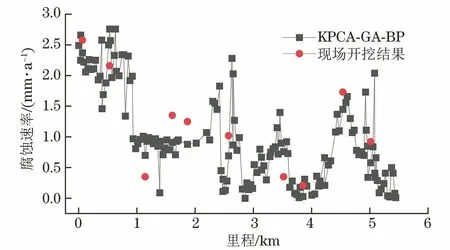
图10 KPCA-GA-BP模型预测结果与现场开挖结果对比Fig.10 Comparison between KPCA-GA-BP model prediction results and field detection results

现场开挖验证结果表明,KPCA-GA-BP模型预测结果比GA-BP和BP模型更接近实际情况,MSE为0.14,即GA 和KPCA 能够能有效提高BP 神经网络在页岩气集输管道腐蚀速率预测中的准确性。可采用KPCA-GA-BP模型预测另一条相邻管道的腐蚀速率,该模型具有一定的参考性和应用价值。

4 结 论

(1) 神经网络可以有效用于页岩气集输管道的内腐蚀速率预测。选择合适的训练方法,构造合适的隐含层具有重要意义。针对此管道,选择Traingdm 作为训练方法,当隐含层节点为(8,1)时,MSE最小。

(2) 遗传算法可以用于优化人工神经网络,选择合适的参数可有效提高预测精度。当进化数为50,种群规模为100,交叉概率为0.3,变异概率为0.2时,MSE 最小为0.21,与优化前的MSE(0.39)相比进一步降低。对于腐蚀机理尚不明确的页岩气集输管道,可采用核主成分分析降维以提高预测精度,输入数据由7个维度降低为4 个维度,模型的MSE进一步降低到0.12。

(3) 利用建立的KPCA-GA-BP 模型对某邻近管道的腐蚀速率进行预测,并取10个点进行开挖验证。验证结果表明,模型具有一定的准确性。在现场实践中,当需要对多条管线进行腐蚀评价时,可以先只对其中一条管线进行检测,将检测结果用于KPCA-GA-BP建模,然后运用该模型实现对其他相邻管线的初步预测。