强化关键能力 突出思维品质

蒋爱萍 胡凯林

作者简介：蒋愛萍，1991年生，湖南永州人，研究生，硕士，一级教师，主要研究方向为中学数学教育教学；胡凯林，1983年生，江西上饶人，研究生，硕士，高级教师，主要研究方向为中学数学教育教学。

摘 要：函数作为高中数学的核心内容，是每年高考考查的必考内容及重点内容。针对近三次教育部组织的高考综合改革适应性测试（2021年八省联考、2023年四省联考、2024年九省联考）及近三年全国六套新高考试题中的函数与导数专题试题，课题组从考查内容和命题特点等方面进行综合分析，提出夯实两个“基本”、深化三类问题、讲透思想方法、加强关键能力、创新试题结构等教学建议。

关键词：高考综合改革；适应性测试；函数与导数；命题特点；教学建议

中图分类号：G63 文献标识码：A 文章编号：0450-9889（2024）08-0067-06

《普通高中数学课程标准（2017年版2020年修订）》（以下简称《课程标准》）指出：“函数是现代数学最基本的概念，是描述客观世界中变量关系和规律的最为基本的数学语言和工具，在解决实际问题中发挥重要作用。”［1］人教A版教材也进一步明确：“客观世界中有各种各样的运动变化现象都表现为变量间的对应关系，这些关系常常可用函数模型来描述。函数思想渗透到数学的各个领域，是进一步学习数学的重要基础。”［2］“导数是微积分的核心内容，蕴含着微积分的基本思想，导数定量地刻画了函数的局部变化，是研究函数增减、最值等性质的基本工具，在实际问题中有着广泛的应用。”［3］因此，函数与导数专题作为高中数学的核心内容，一直是高考数学重点考查的内容。纵观近三年高考的六套新高考卷和近三次教育部组织的高考综合改革适应性测试卷，对函数与导数专题的考查，在考查内容和命题形式等方面有着怎样的规律和创新点？这些规律和创新点对我们今后的教学有着怎样的启示和导向？针对这些问题，本研究做出如下探索分析。

一、考查内容分析

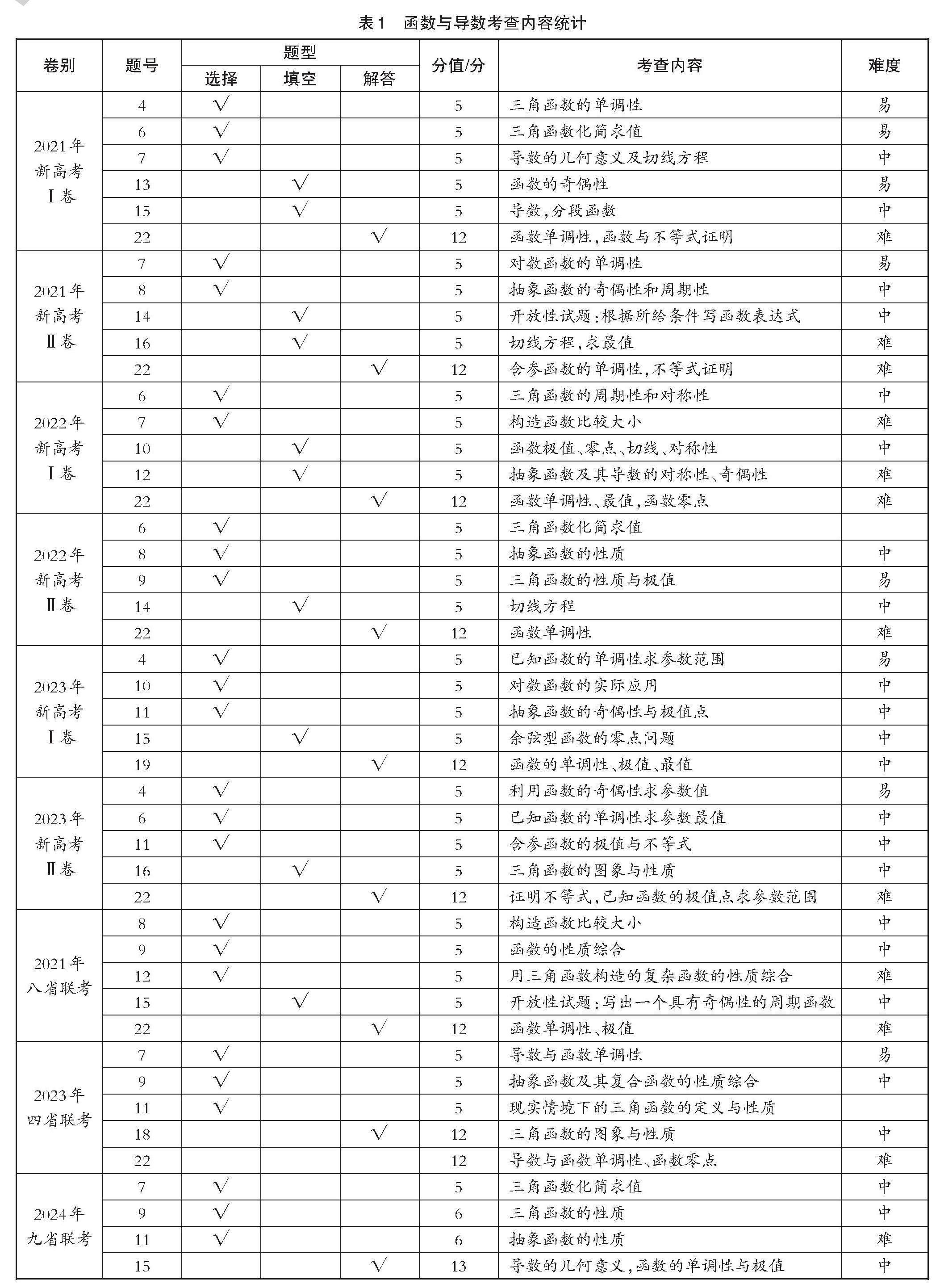
函数与导数考查内容统计表（如下页表1所示）给出了近三年六套新高考卷和近三次教育部组织的高考综合改革适应性测试中的函数与导数专题考查情况统计，根据统计分析得知，函数与导数试题呈现以下特点：

（一）全面覆盖题型，赋分比例较大

2021—2023年全国新高考卷和2021年八省联考中，函数与导数试题一直稳定在5个试题（4小1大），题型覆盖单选题、多选题、填空题、解答题，分值为32分；2023年四省联考函数与导数试题也是5个题（3小2大），分值为39分；2024年九省联考虽然试题总数量减少到19题，但函数试题依然占4个（3小1大），分值为30分。由此我们可以发现，函数与导数专题的考查有着题目数量多、题型覆盖全、赋分比例大等特点，充分体现了函数与导数在高中数学知识中的核心地位。

（二）深化必备知识，贯穿思想方法

综合表1我们可以看出，近三次高考综合改革适应性测试和近三年新高考数学函数与导数试题紧扣《课程标准》和《中国高考评价体系》的要求，试题涉及的主要考查内容可归类为以下八个方面：①函数的图象与函数的性质之间的关系；②函数模型的应用；③导数的几何意义，求曲线的切线方程；④利用导数研究函数的单调性、极值和最值；⑤利用函数的单调性比较实数大小；⑥抽象函数的性质探究；⑦函数的零点讨论；⑧函数与不等式综合。

在全面考查函数主干知识的同时，还加强了对数学思想的考查，试题涉及的数学思想主要有以下五种。①函数与方程思想：例如在解决函数零点以及函数图象交点等问题时，需关注到函数与方程之间的互化，以寻求解决问题的突破口。②数形结合思想：函数图象是函数性质的直观反映，数形结合就是借助函数图象研究函数性质进而解决有关函数的问题。③分类讨论思想：在研究含函数的参数对函数性质的影响时，往往需要对参数进行分类讨论。④转化与化归思想：如函数与方程、函数与不等式之间的等价转化，是研究函数综合问题的重要思路。⑤特殊与一般思想：在抽象函数试题中，如果我们可以找到一个符合条件的具体函数，问题则变得直观且容易作答；又如开放性试题中，根据一类函数满足的共性条件举例写出一个具体函数，也用到了特殊与一般思想。事实上，在具体解决问题时以上数学思想常常交错使用。

（三）强化关键能力，突出思维品质

表1中的函数与导数试题涉及的关键能力主要有逻辑推理能力、数学运算能力、直观想象能力和数学建模能力。近三年新高考试题在函数与导数专题的命题难度合理、层次分明。通过设置多种创新情境，考查学生在情境中提取有用信息、明确问题、分析问题、构建函数、灵活运用多种工具解决问题的能力，进而考查学生的几何直观、数学抽象、逻辑推理和数学运算等数学核心素养。如2023年全国新高考Ⅱ卷第11题，2023年四省联考第11题、第22题，这些试题均通过创设创新试题情境和学科综合情境，体现了较强的综合性和应用性，实现了考查学生的逻辑推理和数学运算等关键能力的目标，突出了考查学生思维的严谨性、科学性和创新性的趋势。

二、命题特点分析

《中国高考评价体系》中的“四翼”考查要求是高考中对素质教育进行评价的基本维度。纵观六套全国新高考数学试卷与近三次教育部组织的高考综合改革适应性测试卷，函数与导数的试题命制旨在落实基础性、综合性、应用性、创新性的考查要求，在试题的结构编排和问题的设计上体现鲜明的数学学科特点，很好地彰显了数学的通用性、严谨性和应用性。此外，函数与导数试题的命制还特别加强了解题思路的多样性和解题方法的灵活性，很好地反映和考查了考生的思维过程。下面通过一些典型试题进行分析说明。

（一）突出基础性要求

基础性体现学科内容的基本性和通用性。函数与导数专题的基础性要求就是突出对函数与导数的基本概念、性质、原理、方法的考查，高考试题的命题特点表现为要求考生深刻理解函数与导数的基本概念、基本原理，整体把握函数与导数的研究内容、研究方法，对教材的知识能举一反三、融会贯通。因此，在适应性测试中我们可以看到，函数与导数试题引导学生重视基础，将所学的基础知识和基本方法内化为关键能力和核心素养，为今后继续学习微积分等高等数学知识内容提供能力铺垫和基础支撑。

例1 （2024年九省聯考第9题）已知函数f（x）=[sin（2x+34π）]+[cos（2x+34π）]，则（ ）

A.函数[fx-π4]为偶函数

B.曲线y=f（x）的对称轴为x=[kπ]，k[∈]Z

C. f（x）在区间[π3，π2]单调递增

D. f（x）的最小值为-2

评析：本题通过正弦型函数与余弦型函数做加法运算构成所要研究的函数，学生需通过辅助角公式对函数进行等价转换，化归为单一的正弦型函数（余弦型函数），进而借助函数y=Asin（[ωx+φ]）的图象与性质进行运算求解。本题以三角函数为载体，考查了函数的奇偶性、对称性、单调性和最值。考查学生运用函数图象研究函数性质的能力，解题入口对考生来说自然、熟悉，试题注重基础知识和通性通法的考查，考生比较容易完成解答。

例2 （2021年八省联考第9题）已知函数f（x）=[xln1+x]，则（ ）

A. f（x）在（0，+[∞]）单调递增

B. f（x）有两个零点

C.曲线y=f（x）在点[12，f12]处切线斜率为-1-ln2

D. f（x）是偶函数

评析：本题通过一次函数与对数型函数做乘法运算构成所要研究的函数，学生首先要利用导数工具求解其单调性、切线斜率以及零点问题，其次需判断该函数的奇偶性。主要考查导数与函数的单调性、导数的几何意义、函数的零点问题、奇偶性的定义及判断方法等基础知识和基本方法，对教学起到了良好的导向作用。

例3 （2024年九省联考第15题）已知函数f（x）=lnx+x2+ax+2在点［2，f（x）］处的切线与直线2x+3y=0垂直。

（1）求a；

（2）求f（x）的单调区间和极值。

评析：此题紧扣《课程标准》，通过基本初等函数的四则运算构建所要研究的函数，第（1）问要求学生求解参数的值，重点考查学生对导数几何意义的理解以及对两直线垂直的充要条件的掌握。第（2）问利用导数求函数的单调区间与极值，较为常规。该题考查导数及其应用，体现了导数解决函数单调性问题、极值问题的一般思路和基本方法，难度适中，有利于考生得分，很好地保持了试卷的整体平稳性。

（二）彰显综合性要求

综合性是高考函数与导数专题的重要考查要求，要求考生在面对错综复杂的问题场景时，能够梳理函数与导数相关的各种知识和原理，综合运用“四基”、实现“四能”。综合性要求体现在对考生综合素质的考查，是高考从知识立意、能力立意到素养立意的转变［4］。函数与导数试题的综合性考查一方面是考查函数与导数内容跟其他各个主题内容（如方程、不等式、数列、解析几何等）的知识交汇和相互综合，另一方面是试题情境涉及数学学科与其他学科情境的综合。除2024年九省联考外，在其余八套试卷中，函数与导数均作为压轴题出现。因此在高考命题中，函数与导数综合问题常常是全面考查学生关键能力和数学思维品质的有效载体，能较好地检验学生的数学学科核心素养，实现新高考试题的区分和选拔功能。

例4 （2023年新高考Ⅱ卷第11题）若函数f（x）=alnx+[bx+cx2]（a[≠]0）既有极大值也有极小值，则（ ）

A.bc＞0 B.ab＞0 C.b2+8ac＞0  D.ac＜0

评析：本题要求考生能准确理解极大值与极小值的概念及其存在的条件，进而将函数的极值问题等价转换为导函数在定义域内有两个变号零点，即方程ax2-bx-2c=0有两个不相等的正实根。本题渗透了转化与化归思想、函数与方程思想，内容丰富、层次分明，具有较高的区分度。此外，本题较好地引导中学数学教学，要求学生从理解概念入手，不断提升学生的分析能力、转化能力、逻辑推理能力和运算求解能力。

例5 （2023年新高考Ⅱ卷第22题）（1）证明：当0＜x＜1时，x-x2＜sinx＜x；

（2）已知函数f（x）=cosax-ln（1-x2），若x是f（x）的极大值点，求a的取值范围。

评析：本题考查构造函数证明不等式问题、复合函数的求导法则，以及导数与函数的单调性和极值之间的关系等。第（1）问利用函数与导数证明不等式，因不含参数，试题难度不大，学生较容易完成，同时为第（2）问的放缩提供了方向和铺垫；第（2）问要求学生能根据题设条件发现偶函数的性质，通过极值的性质对问题进行转化，此问的设计能够让不同学生的理性思维深度、知识掌握程度、运算求解熟练程度都能得到充分展示，对学生的分析能力、转化能力以及思维的灵活性提出了较高要求，体现了高考试题的选拔功能［5］。

（三）体现创新性要求

创新是素质教育的关键特征之一。创新性考查的核心在于对数学创新思维能力的考查，命题创新是完成创新性考查要求的必然途径和具体体现，高考试题在函数与导数的试题设计上通过复杂情境、综合情境和创新试题结构等手段引导考生勇于面对新问题和复杂问题，通过对知识、思想方法的迁移和组合等灵活运用，从而有效解决问题。高考试题从创设新颖的试题情境、新颖的题目条件、新颖的设问方式等三个方面来设计数学创新试题，借此考查考生思维的灵活性与创造性。

1.创新试题情境

例6 （2023年新高考Ⅰ卷第10题）题略。

评析：本题以现实生活中的噪声污染问题为创新情境，考查对数函数的运算性质。

2.创新设问方式

例7 （2021年八省联考第15题）写出一个最小正周期为2的奇函数f（x）=     。

例8 （2021年新高考Ⅱ卷第14题）写出一个同时具有下列性质①②③的函数f（x）：      。

①f（x1·x2）=f（x1）f（x2）；②当x∈（0，+∞）时，f ′（x）＞0；③f ′（x）是奇函数。

评析：此类问题是开放性问题，正确答案不唯一，学生只要熟悉基本初等函数模型，根据题设条件分析函数性质即可作答，考查考生思维的灵活性与创造性。近年来开放性试题难度不大，但是对新高考命题的趋势有积极的导向意义，也为数学学科核心素养的考查提供了新方式。笔者推断有可能是教育部考试中心根据实际调研结果做出的一种新探索，填空题中设置开放性试题很大可能是借鉴解答题中结构不良试题的一种做法。

3.创新题目条件

例9 （2024年九省联考第11题）已知函数f（x）的定义域为R，且[f12][≠]0，若f（x+y）+f（xy）=4xy，则（ ）

A. [f-12=0]    B.[f12=-2]

C.函数[fx-12]是偶函数

D.函数[fx+12]是减函数

评析：在创新题目条件中，抽象函数是近些年高考的热点，抽象函数的题目往往叙述简洁精悍，设计新颖灵活，选项设置符合题目内在逻辑，能多角度考查学生对函数基本概念、基本性质、基本思想方法的理解。学生既可以通过函数相关的必备知识进行逻辑推理和运算求解来完成，也可以通过寻找一个具体函数，将一般转换为特殊，将抽象的函数具体化等灵活多样的方式来求解。因此本题能够较全面地考查学生思维的灵活性以及多样性。

笔者发现，在近三年的新高考卷及2023年、2024年适应性测试卷中均对抽象函数的性质进行了考查，并且均把抽象函数试题放在单选题靠后位置或多选题中，试题中等偏难，侧重考查学生的创新性思维和能力，试题对选拔创新人才起到重要作用。

三、复习备考建议

在“双减”背景下，减轻学生的学业负担，提高数学教学的效益和质量，真正落实“四基”“四能”，培养学生的数学学科核心素养，是一线教师亟需解决的问题。以下将从五个方面给出教学建议。

（一）夯实两个“基本”

函数的基本类型与基本性质是体现函数与导数专题“四翼”考查要求的最重要内容。

1.基本类型：幂函数（尤其是一次函数、二次函数、三次函数、反比例函数）、指数函数、对数函数、三角函数是高中数学教材中重点研究的四大基本初等函数类型。人教A版必修一P92《探究与发现》中说道：“不同的函数通过加、减、乘、除等运算可以构成新的函数，那么，将这两个函数相加构成的函数有哪些性质？这些性质与这两个函数的性质有联系吗？”通过对高考数学试题和适应性测试题分析不难发现，试题中虽然涉及多种类型的初等函数，但都可以归结为以初等函数经过四则运算和复合运算等适當组合后的推陈出新。为此，笔者认为教师在教学过程中要指导学生熟练掌握基本初等函数类型。

2.基本性质：单调性、奇偶性、对称性、周期性、凸凹性、渐近性、极值、最值、零点、拐点等性质是高考命题的主要内容。笔者认为，在这些基本性质教学中，教师一定要让学生认识到四个问题：是什么？为什么？怎么判？有何用？［6］

（二）深化三类问题

函数与导数的综合问题常常围绕“函数的极值最值问题、函数的零点（方程的根）问题、函数与不等式问题”这三类展开。因此笔者认为，首先教师在教学中要以解决问题为抓手，把握问题的实质和数学的本质。其次教师在复习教学中要帮助学生始终厘清以下几个问题：这个问题的本质是什么？这个题目是怎样命制出来的？题目的“根”生长在教材的什么地方？能否进一步推广、变式？

（三）讲透思想方法

数学思想方法是从更高层次的维度对数学知识进行抽象、概括和凝练的结果，它蕴含在知识发生发展和应用的过程中，既是基础知识和基本技能的理论浓缩，又是学生思维品质的良好体现。因此在函数与导数的教学中，教师要把“函数与方程思想、数形结合思想、分类讨论思想、转化与化归思想、特殊与一般思想”贯穿教学的始终，引导和帮助学生将其内化于思维品质，外化于解题习惯。

（四）加强关键能力

在函数与导数高考试题中，主要考查学生的阅读理解、信息整理、抽象概括、直观想象、逻辑推理、运算求解、符号表达等能力。因此，在复习教学中，教师要引导学生在掌握必备知识的基础上，对知识进行迁移和发展，比如借助试题变式、结论推广、条件结论互换等方式培养学生能够在新的情境中解决问题的能力。又如，在遇到一个新的函数时，教师可以引导学生充分体会、想象这个函数的模样，从形和数两个维度启发引导学生思考，让宏观表现和微观验证双管齐下，培养学生的直观想象能力、逻辑推理能力和数学表达能力，进而形成综合应用能力。此外，教师应在信息的阅读与理解、问题的转化与化归、数学思想方法的落实等三个方面下足功夫，引导学生深刻领悟怎样审题，如何寻找解决问题的路径，怎样选择合理的运算路径，指引学生实现从“解题”到“解决问题”的转变。

（五）创新试题结构

在新高考改革背景下，教师要密切关注高考命题的趋势和导向，从被动的解题者转变为主动的命题者。在2024年九省联考测试题中我们不难发现，试题总数变少，多选题和解答题赋分发生调整，函数与导数作为解答题位置前移。无独有偶，在2023年新高考Ⅰ卷中，函数与导数解答题也出现位置前移。同时随着近几年新情境题、开放性试题、结构不良题等创新题在高考试题中层出不穷，我们可以大胆预测：新高考命题的趋势和导向就是要“反题海、反套路、破定势、破形式”，今后高考数学解答题的呈现顺序将不再固定，即不存在所谓的套路或题型固化。因此，盲目刷题、缺少总结反思的复习方式不可取；死记硬背题型、生搬硬套方法的方式行不通；固化思维定式、固守陈旧理念走不远。在日常教学和备考中，教师应有意识地避免思维固化，在扎实构建函数与导数知识体系和数学逻辑的基础上，有计划地逐步加入一些具有综合情境、复杂情境、创新情境、开放情境的问题。另外，教师在教学中应创新思路，通过将已有的问题和结论经过推广、变式、改编等方式形成新的问题链和问题群，让学生收获“一题多链”“一题多解”，在问题链和问题群的解决中进一步提升学生理解问题、分析问题和解决问题的能力，优化学生的思维品质，进而提升学生的数学学科核心素养，助力拔尖创新人才培养。

参考文献

［1］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［M］.北京：人民教育出版社，2020.

［2］人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心.普通高中教科书数学必修第一册［M］.北京：人民教育出版社，2019.

［3］人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心.普通高中教科书数学选择性必修第二册［M］.北京：人民教育出版社，2019.

［4］教育部教育考试院.深入考查基础知识和能力 助力人才选拔和“双减”落地：2023年高考数学全国卷试题评析［J］.中国考试，2023（7）：15-21.

［5］杨林军.注重知识本质理解 强化关键能力考查：2022年高考“函数与导数”专题命题分析［J］.中国数学教育，2022（9）：29-30.

［6］黄厚忠，陈桂明.2021年高考“函数与导数”专题命题分析［J］.中国数学教育，2021（Z4）：24-25.

注：本文系2021年度南宁市教育科学“强基计划拔尖人才培养”专项课题“基于合作学习理念的文科拔尖创新人才培养路径研究”（2021QJ009）的阶段性研究成果。

（责编 林 剑）