基于改进切尾均值的矿井图像去噪算法

熊增举 姚成贵 张德华

文章編号：1671?251X（2024）04?0063?06  DOI：10.13272/j.issn.1671-251x.2024010063

摘要：现有矿井图像去噪算法对于复杂噪声的去除效果有限，且处理速度不能满足实时监控需求。针对该问题，提出一种基于改进切尾均值的矿井图像去噪算法。首先，采用切尾均值滤波器对图像噪声进行初步滤除，同时引入二次检验机制处理残留的噪声点，通过引入离散系数提升算法对不同像素的区分能力，增强去噪性能；其次，采用基于极值数量的分类处理及再次检验机制，有效减少残留噪声问题；然后，在小波函数中引入新的控制变量优化软阈值函数和硬阈值函数，构建双阈值函数，结合 Radon 变换增强对线性特征的处理，增强对矿井图像的检测能力；最后，采用均方误差（MSE）与峰值信噪比（PSNR）进行图像质量评价。实验结果表明：相较于切尾均值算法、硬阈值算法、软阈值算法，基于改进切尾均值的矿井图像去噪算法处理的图像的 MSE增长相对缓慢， MSE 最小，图像去噪效果最好；引入离散系数后，去噪图像的 MSE相较于引入前低300 dB 左右，PSNR 相较于引入前高20 dB 左右，引入离散系数能有效减少噪声点对算法的影响；相较于卡尔曼遗传优化算法、变换域图像去噪算法、交叉分支卷积去噪网络，基于改进切尾均值的矿井图像去噪算法处理的图像 MSE分别降低了27，21，13 dB，PSNR 分别提升了8，6，3 dB，去噪耗时分别缩短了0.20，0.16，0.14 s。

关键词：矿井图像去噪；切尾均值；二次检验机制；小波变换；离散系数；双阈值函数；Radon 变换

中图分类号：TD67  文献标志码：A

A mine image denoising algorithm based on improved trimmed mean

XIONG Zengju1， YAO Chenggui2， ZHANG Dehua3

（1. Department of Electronic Engineering， Jiangxi Vocational and Technical College of Information Application，Nanchang 330043， China；2. College of Data Science， Jiaxing University， Jiaxing 314000， China；3. College of Electrical Engineering， Zhejiang University， Hangzhou 310027， China）

Abstract： The existing mine image denoising algorithms have limited effectiveness in removing complex noise， and their processing speed cannot meet the requirements of real-time monitoring. In order to solve the above problems， a mine image denoising algorithm based on improved trimmed mean is proposed. Firstly， a trimmed mean filter is used to preliminarily filter out image noise， and a secondary inspection mechanism is introduced to handle residual noise points. By introducing discrete coefficients， the algorithm's capability to distinguish different pixels is improved， enhancing the denoising performance. Secondly， a classification processing andretesting mechanism based on the number of extreme values is adopted to effectively reduce the problem of residual noise. Thirdly， new control variables are introduced into the wavelet function to optimize the soft threshold function and hard threshold function， and a dual threshold function is constructed. The method combines with Radon transform to enhance the processing of linear features and enhance the detection capability of mine images. Finally， mean square error （MSE） and peak signal-to-noise ratio （PSNR） are used for imagequality evaluation. The experimental results show that compared to the trimmed mean algorithm， hard threshold algorithm， and soft threshold algorithm， the MSE growth of the mine image denoising algorithm based on the improved trimmed mean is relatively slow， with the smallest MSE and the best image denoising effect. After introducing the discrete coefficient， the MSE of the model is about 300 dB lower than before， and the PSNR is about 20 dB higher than before. Introducing the discrete coefficient can effectively reduce the impact of noise points on the algorithm. Compared with Kalman genetic optimization algorithm， transform domain image denoising algorithm， and cross branch convolutional denoising network， the MSE of the proposed algorithm is reduced by 27， 21， and 13 dB respectively. The PSNR is improved by 8， 6， and 3 dB respectively. The time consumption is shortened by 0.20， 0.16， and 0.14 seconds， respectively.

Key words： mine image denoising; trimmed mean; secondary inspection mechanism; wavelet transform; discrete coefficient; double threshold function; Radon transform

0引言

在矿井监控领域，高质量图像数据对于事故预防和应急响应具有不可替代的作用。然而，矿井低照明、高粉尘等因素会导致监控图像出现大量噪声，使图像质量受到严重影响[1-3]。因此，研发一种适用于矿井环境的高效去噪算法，成为该领域的迫切需求。

矿井环境常见的椒盐噪声、高斯噪声等可能同时出现，且程度不一，传统去噪算法难以同时有效处理多种噪声。当前大多去噪算法没有考虑极端的矿井条件，去噪性能不佳[4]。一些高效去噪技术在处理噪声的同时，会破坏图像的细节和纹理，尤其是在需要保持边缘信息的场景中，如裂缝检测、地形特征分析等[5]。实时监控系统要求算法不仅要保证去噪效果，还要有较快的处理速度，现有算法无法满足实时处理需求[6]。为了解决上述问题，众多学者对图像去噪算法进行了深入研究。霍一等[7]提出一种图像去噪卡尔曼遗传优化算法，该算法对井下椒盐噪声有较好的抑制效果。闫洪波等[8]介绍了一种变换域图像去噪方法，旨在解决煤矿监控图像质量受到椒盐噪声污染的问题，该方法能够保留原始图像的边缘结构信息。程德强等[9]使用交叉分支卷积去噪网络进行图像预处理，提高了井下图像质量。

上述研究主要對矿井图像质量进行提升，但对于复杂噪声的去除效果有限，且处理速度不能满足实时监控需求。鉴于此，本文提出了一种基于改进切尾均值的矿井图像去噪算法。对传统切尾均值算法进行改进，引入二次检验机制，以更有效地识别和处理复杂噪声；结合软硬阈值优化小波变换，在去除噪声的同时，更好地保留图像的细节和边缘信息；通过引入控制系数，调整小波变换的处理强度，在去噪效果和图像质量之间达到最佳平衡。

1矿井图像去噪算法

去噪算法步骤：①采用二次检验切尾均值滤波器对图像噪声进行初步滤除，需确定切尾均值滤波器的窗口模板、步长及移动路径。②引入噪声分类处理思想与二次检验机制，计算统计值离散系数并将其作为判断准则，对可能存在的噪声点进行更精确的处理。③以噪声大小与极值数量为依据，对剩余噪声点采取对应的滤除措施，以改善去噪效果。④在初步去噪的基础上，引入小波变换，利用其高频细节保持能力，通过软硬阈值组合与优化进一步提高去噪性能。⑤使用改进小波阈值函数，引入图像细节和亮度控制，以保持图像细节和纹理质量，同时利用 Radon变换增强对线性特征的处理。⑥通过均方误差和峰值信噪比对去噪图像进行客观质量评价。

1.1切尾均值滤波器

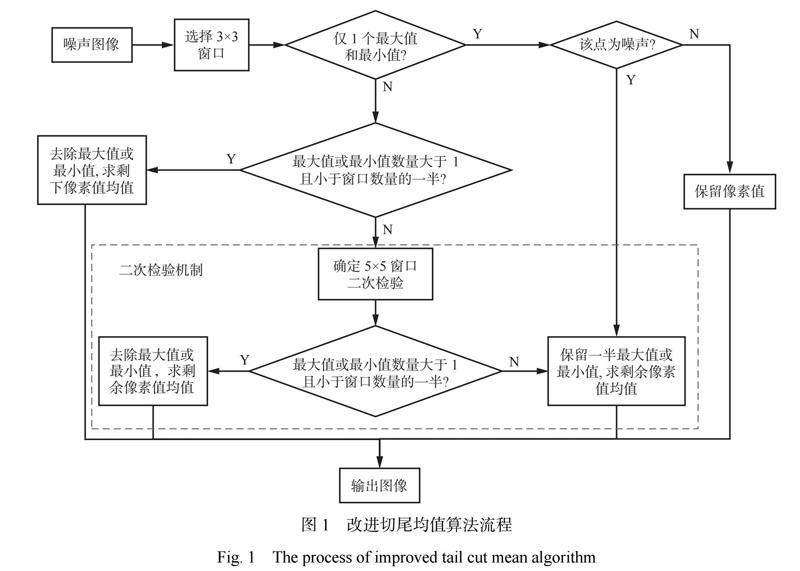
切尾均值滤波器通过切除像素中的极端值，减少或消除图像中的噪声，同时尽量保留图像的细节和结构[10-12]。设置一个移动窗口，将窗口内所有像素值按大小排序，移除窗口中最大和最小的几个像素值，该操作即为切尾操作。切尾操作后，对剩余像素值求平均，用平均值替换中心像素的值。切尾均值滤波虽然能去除离群点造成的噪声，但同时也可能会删减图像的重要细节，如高亮区域或暗部的细节信息。切尾均值滤波窗口的大小是预设的，不会根据像素邻域内的实际噪声状况动态调整，这可能导致滤波效果不理想。此外，切尾均值滤波可能会使图像边缘变得模糊，因为强边缘灰度变化范围更大，可能被当作噪声去除掉。针对上述问题，对切尾均值算法进行改进，改进算法流程如图1所示。

改进切尾均值算法的具体步骤如下：

1）设定一个3×3的矩阵滤波窗口，通过该窗口对图像像素值排序，同时统计最大值或最小值的数量。

2）如果矩阵滤波窗口中仅含有1个最大值或最小值，则根据预设的判断准则判断该点是否为噪声点。

3）根据矩阵滤波窗口中极值的数量决定是否需要使用5×5的矩阵滤波窗口进行处理，如果最大值或最小值的数量过半，则舍弃这些值并将剩余像素值的均值作为输出。

4）引入统计值离散系数衡量处理前后2组数值之间的差异，并使用该系数对噪声去除操作的精确性进行优化。

离散系数用于衡量数据分布的相对离散程度。如果标准差较大，意味着数据点与均值之间的差异较大，数据的波动范围宽；反之，如果标准差较小，则数据点相对靠近均值，波动范围窄。在图像去噪算法中，离散系数用于评估像素值的波动程度。如果某个像素周围的离散程度高，则该点更可能是噪声。反之，波动小的区域可能代表图像中的细节或结构。因此，在决定是否去除某个像素点时，可使用离散系数作为参考，在保留重要图像特征的同时，去除真正的噪声。

1.2改进小波阈值函数

在矿井图像处理中，小波变换能够识别图像中的特定模式或异常情况，如裂缝、矿层不连续性等[13-15]。在低频率下，小波变换可以提供宽范围的分析窗口，有助于识别矿井图像中的大尺度结构特征。而在高频率下，小波变换则可提供窄范围的分析窗口，有利于检测图像中的细节和微小变化。此外，利用小波变换的去相关性可从图像中分离出有用信号和无关噪声[16-18]。但小波函数中的软阈值函数具有恒定误差，用软阈值函数去噪的图像边缘细节会出现丢失情况。小波变换中的硬阈值函数具有不连续性，用硬阈值函数去噪的图像可能引入不自然的视觉瑕疵[19-21]。

为优化软阈值函数和硬阈值函数，引入2种控制变量和β。用于控制图像细节，取值过大，会导致图像细节丢失；β用于控制图像亮度。构建新的双阈值函数：

式中：W为小波变换系数的幅值；T 为阈值。

由式（1）可知：当=0时，双阈值函数为硬阈值函数；当=1且β接近1时，双阈值函数为软阈值函数。和β可根据图像的内容特点取值。例如，在裂缝和矿层不连续等区域增大，以便更好地保留细节信息；而在大尺度结构特征较为重要的区域，可以减小。本文中取=0.02，β=0.2。

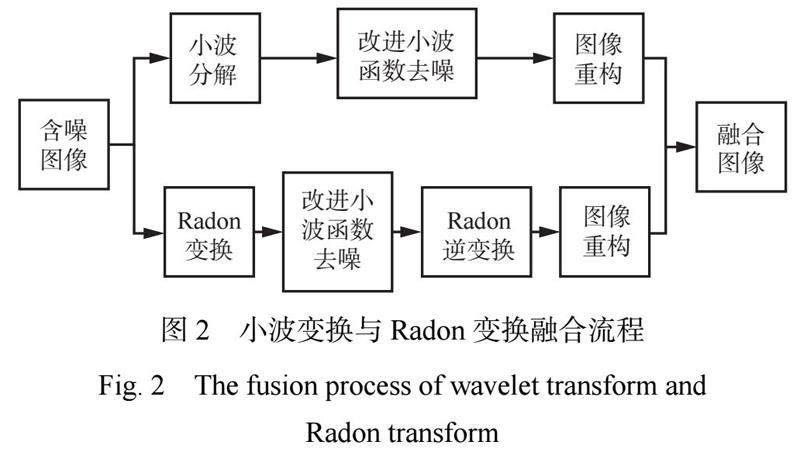
在二维噪声图像中往往存在2种奇异数据，即点奇异数据和线性奇异数据[22-23]。在小波变换中，点奇异数据具有较好的检测效果，但线奇异数据检测效果较差[24-25]。因此，采用 Radon变换对图像进行处理。 Radon 变换主要用于计算图像的投影数据。将 Radon变换用于检测图像中的直线特征、强化图像中线性细节、减小图像去噪过程中的细节损失等具有较好效果。将小波变换与 Radon变换进行融合，流程如图2所示。

2实验分析

实验图像来自山西某矿井视频监控图像，图像尺寸包括12.7 cm×8.9 cm，17.8 cm×12.7 cm，20.3 cm×15.2 cm 三种，每种尺寸的图像均选取200张。在 Matlab 中使用内置函数添加各种类型的噪声，如采用 imnoise 函数添加高斯噪声、脉冲噪声等。

2.1改进切尾均值和小波双阈值函数效果验证

分别采用切尾均值算法、硬阈值算法、软阈值算法、本文算法对图像进行去噪，通过比较去噪前后的均方误差（Mean-Square Error，MSE）和峰值信噪比（Peak Signal-to-Noise Ratio，PSNR），评估算法的有效性。4种算法的去噪效果如图3所示，可看出，本文算法对矿井图像的去噪效果更加明显，在光线不足的环境中图像更加清晰、质量更高。

不同算法去噪图像的 MSE 和 PSNR 如图4所示。从图4（a）可知，随着噪声密度增大，本文算法去噪图像的 MSE 增长相对缓慢，MSE 最小，图像去噪效果最好；切尾均值算法去噪图像的 MSE 增长迅速，且在噪声水平相对较高时 MSE 超过1100 dB；硬阈值算法去噪图像的 MSE 虽然增长较缓，但噪声密度达到0.30时 MSE 接近900 dB。由图4（b）可知，尽管切尾均值算法和硬阈值算法去噪图像的 PSNR 下降较平缓，但都显著低于本文算法。

2.2离散系数效果验证

为验证离散系数的效果，对引入离散系数前后去噪算法处理后图像的 MSE 和 PSNR 进行对比分析，结果如图5所示。去噪算法引入离散系数后，去噪图像的 MSE 相较于引入前低300 dB 左右，PSNR 相较于引入前高20 dB 左右。实验结果表明，引入离散系数能有效减少噪声点对算法的影响。

2.3算法耗时

去噪算法的性能不仅取决于其去噪效果，也取决于算法的运行速度，耗时反映了算法的效率。选取2幅噪声较大的矿井图像，对切尾均值算法、硬阈值算法、本文算法的平均耗时进行统计，结果如图6所示。可看出对于图像1，切尾均值算法、硬阈值算法、本文算法平均耗时分别为3.91，4.58，3.49 s；对于图像2，切尾均值算法、硬阈值算法、本文算法平均耗时分别为3.82，3.66，2.91 s。本文算法耗时最短，效率最高。

2.4对比分析

为进一步验证研究算法的先进性，将本文算法与文献[7]—文献[9]提出的卡尔曼遗传优化算法、变换域图像去噪算法、交叉分支卷积去噪网络进行对比，图像噪声密度取0.30，以图像2作为实验样本，结果见表1。可以看出4种算法的性能差距虽然较小，但是本文算法具有相对较好的表现。相较于卡尔曼遗传优化算法、变换域图像去噪算法、交叉分支卷积去噪网络，本文算法去噪图像的 MSE 分别降低了27，21，13 dB；PSNR 分别提升了8，6，3 dB；去噪耗时分别缩短了0.20，0.16，0.14 s。实验结果验证了本文算法的先进性与可靠性。

3结论

1）提出了一种基于改进切尾均值的矿井图像去噪算法。对传统的切尾均值算法进行改进，引入了基于噪声点特征的分类处理思想，通过引入2個控制系数对小波变换的软硬阈值函数进行优化。

2）实验结果表明：相较于切尾均值算法、硬阈值算法、软阈值算法，基于改进切尾均值的矿井图像去噪算法处理的图像的 MSE 增长相对缓慢，MSE 最小，图像去噪效果最好；引入离散系数后，去噪图像的 MSE 相较于引入前低300 dB 左右，PSNR 相较于引入前高20 dB 左右，引入离散系数能有效减少噪声点对算法的影响；相较于卡尔曼遗传优化算法、变换域图像去噪算法、交叉分支卷积去噪网络，本文算法处理的图像的 MSE 分别降低了27，21，13 dB， PSNR 分别提升了8，6，3 dB，去噪耗时分别缩短了0.20，0.16，0.14 s。

3）基于改进切尾均值的矿井图像去噪算法对于极端条件下的噪声处理效果仍有待验证，例如在极低或极高亮度条件下的去噪效果。后续工作将着重于优化算法对不同光照条件和更广泛噪声类型的适应性。此外，进一步降低算法计算复杂度，提高其在大规模数据处理中的实用性，也是重要的研究方向。

参考文献（References）：

[1] DHAS M M，SINGH N S. Image denoising using discrete wavelet transform and adaptive thresholding optimised with improved arithmetic optimisation algorithm and guided filter[J]. International Journal of Computational Intelligence Studies，2022，11（2）：131-156.

[2] ZHU Yun，GONG Chengjian，LIU Shuwen，et al. Infrared object detection via patch-tensor model and image denoising based on weighted truncated Schatten-p norm minimization[J]. IET Image Processing，2023，17（6）：1762-1774.

[3] WANG Yingmei，WANG Zhendong. Image denoising method based on variable exponential fractional-integer- order  total  variation  and  tight  frame  sparse regularization[J]. IET Image Processing，2021，15（1）：101-114.

[4] DHILLON D，CHOUHAN R. Edge-preserving image denoising using noise-enhanced patch-based non-local means [J]. Multimedia Systems，2023，29（3）：1025-1041.

[5] REKHA H，SAMUNDISWARY P. Image denoising using fast non-local means filter and multi-thresholding with  harmony  search  algorithm  for  WSN[J]. International  Journal  of  Advanced  Intelligence Paradigms，2023，24（1/2）：92-109.

[6] WANG Qinglin，BAI Qing，LIU Yuting，et al. SNR enhancement for BOTDR with spatial-adaptive image denoising  method[J]. Journal  of  Lightwave Technology ：A Joint IEEE/OSA Publication，2023，41（8）：2562-2571.

[7]霍一，马晓轩.卡尔曼滤波结合遗传算法的矿井图像去噪算法研究[J].计算机应用与软件，2022，39（2）：220-227.

HUO Yi， MA Xiaoxuan. Mine image denoising algorithm based on Kalman  filter and genetic algorithm[J]. Computer Applications and Software，2022，39（2）：220-227.

[8]闫洪波，赵蓬勃，刘恩佐，等.二维变分模态分解矿井监控视频图像去噪[J].计算机应用与软件，2023，40（6）：211-215.

YAN Hongbo，ZHAO Pengbo，LIU Enzuo，et al. Two- dimensional variational mode decomposition for mine monitoring video image denoising[J]. Computer Applications and Software，2023，40（6）：211-215.

[9]程德強，王雨晨，寇旗旗，等.基于改进深度残差网络的矿井图像分类[J].计算机应用研究，2021，38（5）：1576-1580.

CHENG Deqiang，WANG Yuchen，KOU Qiqi，et al. Classification of mine images based on improved deep residual  network[J]. Application  Research  of Computers，2021，38（5）：1576-1580.

[10]孙峰，李博，高紫俊，等.一种基于 Retinex 理论矿井下图像增强算法[J].大连工业大学学报，2023，42（2）：151-156.

SUN Feng，LI Bo，GAO Zijun，et al. A mine image enhancement algorithm based on Retinex theory[J]. Journal of Dalian Polytechnic University，2023，42（2）：151-156.

[11] SINOVA B. On depth-based fuzzy trimmed means and a notion of depth specifically defined for fuzzy numbers[J]. Fuzzy Sets and Systems，2022，443：87-105.

[12] XU Yanlei，WANG Xindong，ZHAI Yuting，et al. Precise variable spraying system based on improved genetic  proportional-integral-derivative  control algorithm[J]. Transactions  of the  Institute  of Measurement and Control，2021，43（14）：3255-3266.

[13]文小波. M 估计下切尾均值和平尾均值的抽样分布[J].湖南文理学院学报（自然科学版），2020，32（1）：4-8，94.

WEN Xiaobo. Sampling distribution of trimmed mean and winsorised mean of M estimator[J]. Journal of Hunan University of Arts and Science（Science and Technology），2020，32（1）：4-8，94.

[14] BORISCH E A，FROEMMING A T，GRIMM R C， et al. Model-based image reconstruction with wavelet sparsity regularization for through-plane resolutionrestoration in T2-weighted spin-echo prostate MRI[J]. Magnetic Resonancein Medicine：Official Journal of the Society of Magnetic Resonance in Medicine，2023，89（1）：454-468.

[15] SHAH S A A，BAIS A，ALASHAIKH A，et al. Discrete wavelet transform based branched deep hybrid network for environmental noise classification[J]. Computational Intelligence，2023，39（3）：478-498.

[16] WANG Juan. Application of wavelet transform image processing technology in financial stock analysis[J]. Journal of Intelligent & Fuzzy Systems：Applications in Engineering and Technology，2021，40（2）：2017-2027.

[17] SINGH P，DIWAKAR M. Wavelet-based multi-focus image fusion using average method noise diffusion （AMND）[J]. Recent Advances in Computer Science and Communications，2021，14（8）：2436-2448.

[18] WANG Siyuan， LYU Junjie， HE Zhuonan， et al. Denoising auto-encoding priors in undecimated wavelet domain  for  MR  image  reconstruction[J]. Neurocomputing，2021，437（4）：325-338.

[19] JIANG Yanhua，LAN Guanglin，ZHANG Zhiqing. Ship engine detection based on wavelet neural network and FPGA image scanning[J]. Alexandria Engineering Journal，2021，60（5）：4287-4297.

[20] VAIYAPURI T，ALASKAR H，SBAI Z，et al. GA- based multi-objective optimization technique for medical image denoising in wavelet domain[J]. Journal of Intelligent & Fuzzy  Systems： Applications  in Engineering and Technology，2021，41（1）：1575-1588.

[21] SRIDHAR B. A wavelet based copyright marking on image under sub-bands stacking technique[J]. Latin American Applied Research，2021，51（1）：71-75.

[22] SOLAK A，CEYLAN R，BOZKURT M A，et al. Adrenal tumor segmentation on U-Net：a study about effect of different parameters in deep learning[J]. Vietnam Journal of Computer Science，2024，11（1）：111-135.

[23] ZHAO Yan，GUO Ming，CHEN Xiangyong，et al. Attention-based CNN fusion model for emotion recognition during walking using discrete wavelet transform on EEG and inertial signals[J]. Big Data Mining and Analytics，2024，7（1）：188-204.

[24] LIU Meng，MENG Kexin，XING Ruyi，et al. Haar wavelet transform and variational iteration method for fractional option pricing models[J]. Mathematical Methods in the Applied Sciences，2023，46（7）：8408-8417.

[25] CHHA H，PENG Yongbo. Adaptive linear quadratic regulator for optimal structural control based on wavelet transform and  genetic algorithm[J]. Engineering Computations：International Journal for Computer-Aided Engineering and Software，2023，40（4）：1016-1039.