逆向教学思维下的小学数学“教—学—评”一体化教学设计<br/>——以四年级下册“三角形”为例

逆向教学思维下的小学数学“教—学—评”一体化教学设计
——以四年级下册“三角形”为例

2024-05-25文|袁芳

新课程 2024年8期

文| 袁芳

常规教学思维下的小学数学教学关注教学任务、教学活动的设计，忽视学生发展需求和教学评价的重要性，在一定程度上影响学生对自身学习情况的客观认识，继而影响教学效果。教师教学、学生学习、教学评价三项教学工作是不可分割的，教师只有认识到这一点，并根据具体教学需要设计教学方案，才能保证学生在教学中取得丰富收获。教师有必要逆转教学思维，基于实际教学情况反思教学要达到怎样的目的、怎样判断学生是否实现了教学目标、如何引导学生实现教学目标等，并基于逆向教学思维设计“教—学—评”一体化教学方案，使教师教学、学生学习、教学评价三者成为一个有机的整体，为提高学生的数学课程学习效果创造良好的教学环境。为此，本文以四年级下册“三角形”单元教学为例，探究逆向教学思维下的小学数学“教—学—评”一体化教学设计策略。

一、目标设计

为了实现小学数学“教—学—评”一体化，教学目标必须有以下特点：（1）可以确定学生应当学习哪些内容；（2）可以确定学生对教学内容的接受程度；（3）所整理的教学内容是可以传授给学生的；（4）教学目标具有确定性，可以作为评价任务的设计参考。由此，在“三角形”单元教学目标设计阶段，教师应做好课程标准、教材内容、学生学情分析工作，并综合分析结果设定教学目标。

（一）分析课程标准

《义务教育数学课程标准（2022 年版）》（以下简称“新课标”）针对“三角形”的学业要求有：（1）能直观描述三角形的特征；（2）知道三角形任意两边之和大于第三边；（3）会根据角的特征对三角形分类，认识直角三角形、锐角三角形和钝角三角形；（4）能根据边的相等关系，认识等腰三角形和等边三角形；（5）知道三角形的内角和是180°；（6）探索并掌握多边形的内角和公式。

基于新课标的分析结果，教师可以明确学生在“三角形”教学中应当学习的具体内容。

（二）教材分析

“三角形”单元学习内容的编排建立在“平行四边形和梯形”等内容基础上，对三角形的稳定性、三角形三边关系、三角形分类、三角形内角和及多边形内角和展开介绍，一方面用文字、数学符号概述有关三角形的数学规律，另一方面借助图形、案例进行说明，为学生后续学习“多边形的面积”“长方体与正方体”等单元内容奠定基础。

基于教材内容分析结果，教师整理出可以传授给学生的重要知识点。

（三）学情分析

四年级学生经过两个学段的学习，对三角形已经有了直观认识，能够从平面图形中分辨出三角形，且掌握了角度测量、边长测量、数学计算的方法与技巧。但是，此阶段的学生对三角形的分类、三角形内角和规律缺乏认识。

基于学情分析结果，教师可以确定学生能够接受图形的观察、图形规律的探究等教学内容，有能力基于已掌握的图形观察、测量、研究方法探究三角形的性质、三边关系等。

（四）教学目标

1.明确三角形的稳定性，知道三角形两边之和大于第三边，知道三角形内角和为180°。

2.学会根据角的特点区分锐角三角形、直角三角形、钝角三角形；学会根据边的特点区分等腰三角形、等边三角形。

3.学会应用拼摆、猜想、设计等方法探究三角形特征，并由此总结出图形研究的通性通法，提高观察图形与动手操作能力。

二、评价任务设计

逆向教学思维下的“教—学—评”一体化教学设计中，教师在明确学生应达成怎样的学习目标以后，还应设计判断学生是否达成学习目标的评价任务，确定学生的发展情况，并根据评价结果调整教学细节，改进教师教学与学生学习的方式。评价任务的设计要参考教学目标，还要联系评价方法、评价结果呈现与反馈等要素。逆向教学思维下的评价任务设计思路如下（见表1）。

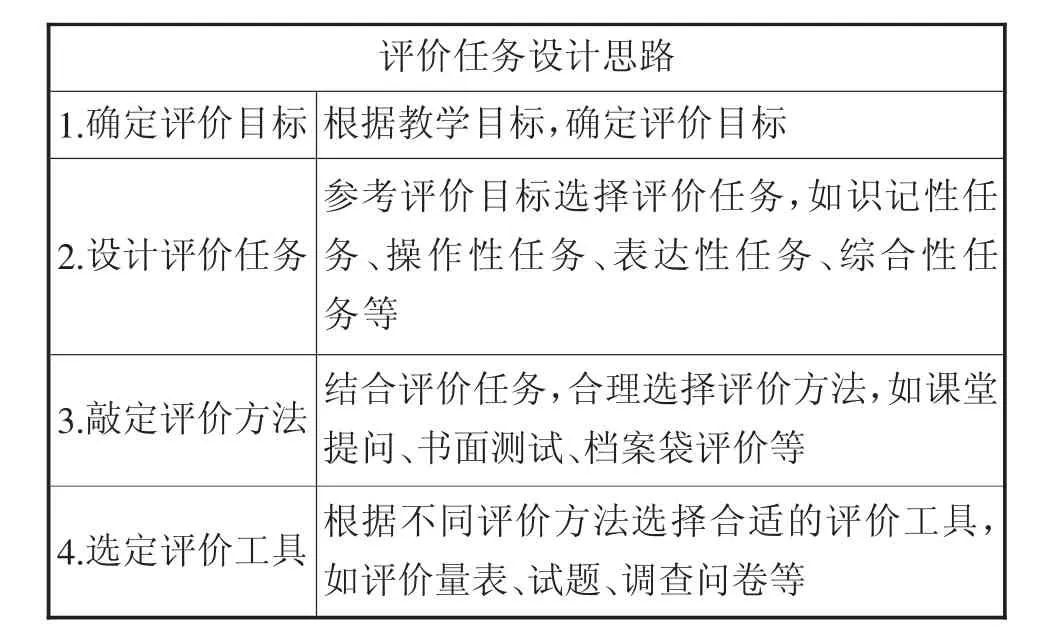
表1

以四年级下册“三角形”单元教学评价任务设计为例，教师可设计如下评价任务（见表2）。

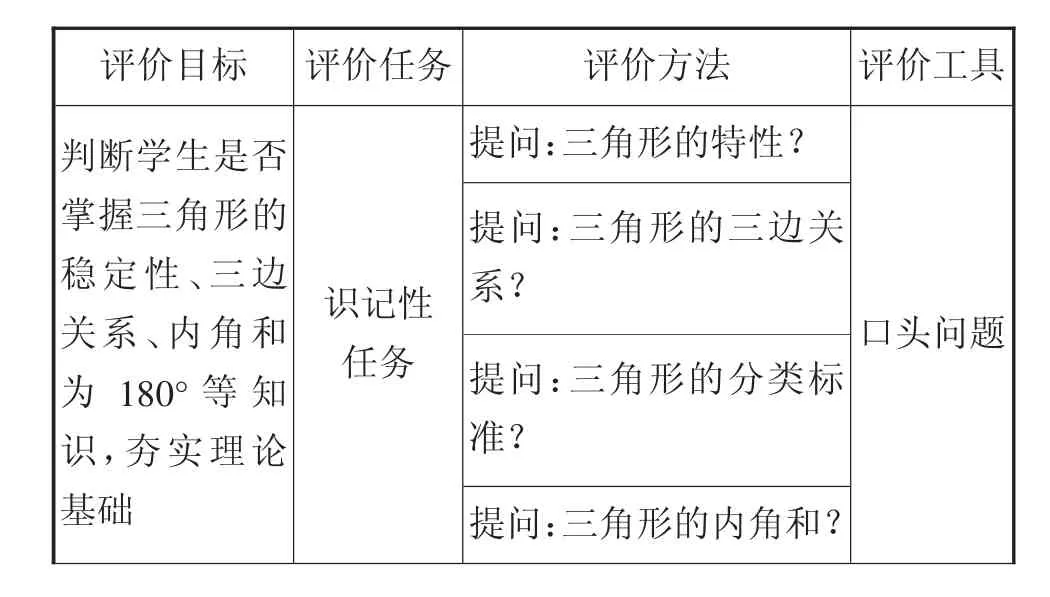
表2

三、教学活动设计

逆向教学思维下的“教—学—评”一体化教学设计中，教师需要思考如下问题：哪些学习体验和教学能够使学生达到预期的学习目标？哪种方式可以使学生对教学内容产生兴趣？怎样教学可以驱动学生分享自身的学习观点？什么样的活动可以使学生自主参与到数学规律的探究过程中？基于上述问题，教师再结合教学目标、评价任务设计，能够使学生达成学习目标的教学活动，确保教师教学、学生学习与评价反馈成为有机的整体。

以四年级下册“三角形”单元教学为例，教师可以先后设计对比、讨论、分类、操作、练习教学活动，并将教学评价应用到各活动当中，及时与学生交流、反馈，指导学生先了解三角形具有稳定性、三角形的三边关系、三角形的内角和等知识，促进学生内化、吸收，提高单元教学效果。具体设计内容如下所示。

（一）对比活动

结合教材，组织学生对比观察图片内容（见图1），引导学生初步认识三角形。

图1 生活中的三角形

教师指导学生观察空调外机、塔吊、电线杆上的三角形，引导其分析：三角形在这些事物中起到什么作用，如果将三角形换成平行四边形，是否还可起支撑、稳定作用？经观察对比，学生明确：三角形具有稳定性。在此期间，教师观察学生是否积极参与到图片观察、对比活动当中，能否快速辨别图片中的三角形，是否能基于“平行四边形不稳定性”迁移“三角形具有稳定性”这一知识点，判断学生是否掌握三角形的性质，是否可以开展后续教学活动。

（二）讨论活动

围绕“三角形任意两边的和大于第三边”这一重点知识，教师可结合生活案例出示图片（见图2），提出问题，组织讨论，引导学生探究。

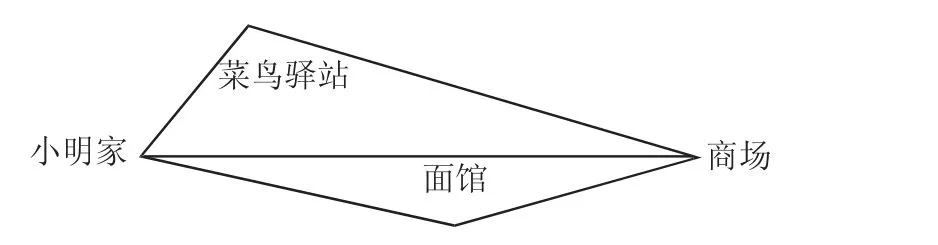
图2

师：小明由家至商场共有三条路，哪条路最近？

生：最中间的那条路最近，因为两点之间，线段最短。

师：观察图形，你能推断出什么？

生：三角形的两边之和一定大于第三边。

教师围绕图片组织讨论，激活学生的直观思维，使其在观察的过程中发现几何规律，完成对“三角形”教学重点的初步探索。在此活动中，教师观察学生是否主动参与讨论，是否采取画草图、用刻度尺测量等探究学习行为，是否在对比数据的过程中总结数学规律等，及时做出评价反馈，端正学生的探究行为，使其学会基于直观现象、客观数据分析几何图形特征，形成数学探究能力。