岩溶隧道对地下水环境影响分析及涌水量预测研究

2024-05-23王超林黄小龙刘腾龙

贵州大学学报(自然科学版) 2024年2期

胡颢,王超林*,黄小龙,党爽,刘腾龙

(1.贵州大学土木工程学院,贵州贵阳 550025;2. 湖南省城市地质调查监测所,湖南长沙 410007)

地下水是影响隧道安全施工的一个重要影响因素。尤其在岩溶发育的区域,地下水不仅危及施工安全、影响施工进度,而且在隧道施工期大量输排地下水情况下极大地恶化当地环境[1]。为减少或进一步消除隧道开挖对生态、地质环境和人类社会负面影响,充分认识岩溶地下水系统在隧道工程干扰下的行为和恢复能力是十分必要的。胡伟等[2]以重庆主城拟建鹿角隧道为例,通过科学分析及现场调查,对拟建隧道的影响范围及易引起的地下水环境效应进行评价。刘志春等[3]研究了多种工程因素对地下水资源流失量及水位变化的影响规律。康小兵等[4]采用Visual Modflow可视化三维软件,模拟3种方案(天然条件、隧道开挖、隧道运营)下5种不同工况隧道建设对地下水环境的影响;罗云菊等[5]依据重庆南山地勘资料,研究了岩溶槽谷区既有多条隧道条件下拟建隧道施工(不考虑和考虑防水措施)时的区域渗流特征。

隧道开挖除了对地下水环境造成影响,涌水问题也是隧道建设施工过程中的一项重大安全问题,为了保证隧洞施工的工程安全和生态与经济效益,在隧道开挖前对涌水量进行预测与计算是至关重要的。以前学者主要运用水文地质比拟法[6-7]、水均衡法去预测隧道涌水量。但是水均衡法只适用于地质结构简单的地区,水文地质类比法预测的精度主要是取决于两工程的相似性。岩溶地区地质结构复杂,而且每个地区岩溶发育情况不尽相同,多数情况下以上两种方法并不适用。随着计算机技术的提高,数值法在隧道涌水量预测方面得到了广泛应用。江思珉等[8]利用有限差分程序Modflow模拟计算基岩裂隙含水介质中深长隧道开挖的涌水量。王纯祥等[9]利用地理信息系统(geographic information system,GIS)和三维快速拉格朗日有限差分法(fast lagrangian analysis of continua,FLAC3D)对日本九州地区新干线筑紫隧道涌水及其对地下水位的影响进行分析。郭纯青等[10]采用流量衰减分析法、物理模拟和反向传播(back propagation,BP)神经网络模型三者相结合的方法,对岩溶隧道涌水量进行综合预测研究。尽管迄今为止对隧道施工造成的地下水环境影响和隧道涌水两个方面已开展了大量研究[11-17],但由于各个地区水文地质条件相差甚远,隧道开挖过程中对地下水环境的影响也并不相同。因此,对即将开挖隧道的地区进行隧道涌水量、影响范围等预测分析是必不可少的。

本文以重庆主城区拟建鹿角隧道为例,运用水文地质分析和数值模拟的方法分析其隧址区在鹿角隧道扰动下的地下水行为,并采用地下水径流模数法、数值模拟法对隧道进行最大涌水量预测。为隧道地下水环境影响科学评价及隧道设计、施工提供理论基础,也可为岩溶地区隧道开挖实践中的地下水、生态和地质环境保护提供重要参考。

1 隧址区概况

1.1 工程概况

鹿角隧道为分离式双洞双向六车道隧道,净宽13.0 m,净高8.0 m,洞间距42 m,设计速度60 km/h,双向6车道。设计起点路面高程252.056 m,终点路面高程336.266 m,设计终坡2.5%。

1.2 自然地理及工程地质条件

鹿角隧道位于重庆市巴南区和南岸区交界的南山山脉,西起重庆市南岸区重庆市交通大学,东至重庆市巴南区内环快速路鹿角立交附近,如图1所示。隧址区属亚热带季风性湿润气候,降雨多集中在5—9月,约占全年降雨量的70%;年最大降雨量1 544.8 mm,年最小降雨量740.1 mm。隧址区内支流主要有花溪河、苦溪河,大体上沿北东—南西向发育,受季节性降雨影响较大。

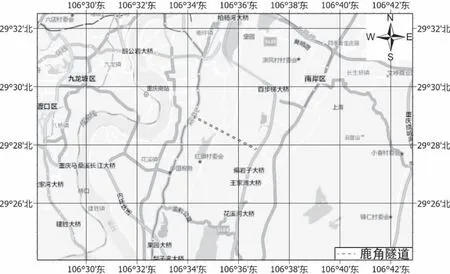
图1 隧道位置图Fig.1 Tunnel location map

鹿角隧道隧址区构造属剥蚀条带状低山地貌,海拔高程在280～580 m范围内。受构造的控制和岩性的制约,形成了“一山两槽三岭”的地貌景观。图2为隧道穿越地层的地质剖面图,核部为三叠系下统飞仙关组(T1f),两翼依次为三叠系中统雷口坡组(T2l)、下统嘉陵江组(T1j)、上统须家河组(T3xj)、侏罗系中下统自流井组(J1-2z)、中统新田沟组(J2x)。

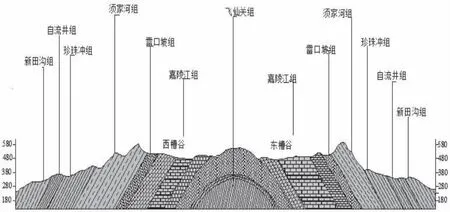
图2 地质剖面图Fig.2 Geological profile map

1.3 水文地质条件

根据地下水赋存条件,可将隧址区内地下水分为潜水和承压水两类,以下伏飞仙关四段(T1f4)为界,下部飞仙关组三段(T1f3),属可溶岩类含水岩组,为承压含水层。上部嘉陵江组一段(T1j1)灰岩和雷口坡组(T2l)的白云质灰岩具有强富水性,属可溶岩类含水岩组,为潜水含水层,地下水埋深浅;两翼含水岩组主要为分布厚度较大的三叠系上统须家河组(T3xj)砂岩,富水性中等,属碎屑岩类裂隙含水岩组,为潜水含水层。侏罗系下统珍珠冲组(J1z)、中下统自流井组(J1-2z)、中统新田沟组(J2x)的泥岩、页岩、砂岩、介壳灰岩、泥质灰岩富水性较弱,为弱富水的碎屑岩类裂隙含水岩组,相对须家河组砂岩含水层为相对隔水层。

在隧址区特定的构造条件下,东西方向上,由于须家河组地层构成山脊所隔,须家河组一段(T3xj)页岩起隔水作用,隧址区可溶岩地下水主要沿雷口坡(T2l)和嘉陵江地层(T1j)分布。南北方向上,由于南山隧道修建,南山隧道位于水平径流带内,改变了地下水的径流条件,成为一个排泄通道,在南山隧道两侧形成降落漏斗,造成地下水分水岭南移,根据地表调查推测现地下水分水岭位于重庆邮电大学附近。隧址区在北侧分水岭、槽谷两侧隔水层控制下,地下水在岩溶槽谷中沿地下河或溶隙由北向南纵向径流,向区域地下水排泄基准面(花溪河)排泄。

2 模型的建立

2.1 水文地质概念模型

2.1.1模拟范围及边界条件概化

鹿角隧道地下水三维数值模型的范围为整个鹿角隧道沿线,北至地下水分水岭,南至花溪河,如图3所示。模型的东、西两侧为低水位边界且与核部区域存在水力联系,因此,将东、西两侧概化为定水头边界。而模型的北侧为地下水分水岭,作为零流量边界;南侧为花溪河排泄基准面,作为定水头边界处理。隧址区内钻孔多分布在隧道两侧,为了建立与实际地质情况相符的三维地质模型,根据隧址区水文地质图及鹿角隧道地质断面图插入适量的虚拟钻孔,通过地下水模拟系统(groundwater modeling system,GMS)中Boreholes、Solid等模块生成了隧址区的三维地质模型,如图3所示。

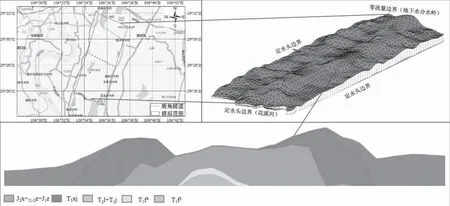
图3 模拟区域和三维地质图Fig.3 Simulation area and 3D geologic map

2.1.2含水层及初始条件概化

隧址区内主要的含水地层为三叠系中统雷口坡组(T2l)和下统嘉陵江组(T1j),为潜水含水层。三叠系下统飞仙关组(T1f3)地层具有承压性,但富水性中等,含水并不丰富,为承压含水层。而山体东、西两侧的三叠系上统须家河组(T3xj)地下水活动性相对可溶岩较差,可视为中弱透水层。鹿角隧道修建之前,东西两槽谷内出露地表的水点众多,因此,整体上为高水位槽谷,在隧道所经过的含水系统内可以近似的认为地表高程与地下水位十分接近。

2.1.3源汇项的概化

隧址区内主要接受大气降雨补给,区域内多年平均降雨量1 163.3 mm,降雨主要分布在雨季(5—9月),约占全年降雨降雨量的70%。排泄项主要包括蒸发、暗河和地表溪流。

2.2 三维数值模型的建立

2.2.1网格剖分及参数选取

根据前文中所描述的水文概念模型将模拟区剖分为150×150×1共22 500个网格,其中,有效单元格为10 181个。各地层渗透系数K取值基于水文地质试验,结合重庆地区经验及相似工程的参数取值结果进行一定的概化,在模型参数取值时,由于岩溶发育的各向异性,将渗透系数赋值尽量符合南山地区实际水文地质情况,并通过软件自带的PEST模块对参数进行校正,最终得到的参数如表1所示。

表1 隧址区渗透性模拟计算参数Tab.1 Simulation calculation parameters for permeability of tunnel site area

2.2.2模型的校验

通过隧址区的七个观测孔的实测水位对模型进行的校验,拟合情况如表2所示。由表2可知,经过模型模拟计算所得的观测井水位与实测观测井水位存在误差,但是误差在一个合理的比例范围之内(0.01%～0.22%)。模型拟合精度较高,所建模型和实际地下水渗流情况较为相符,后续研究分析将在此模型基础上进行。

3 隧道对地下水环境的影响分析

3.1 隧道修建对地下水环境影响规律

3.1.1天然渗透场模拟

根据前述参数以及边界条件设置,得到隧址区的天然状态下地下水渗流场,如图4所示。其中,雷口坡和嘉陵江地层(T2l+T1j)可溶岩地层出露的背斜核部地下水水位较高,两翼非可溶岩地层水位高于核部可溶岩地层。区域内地下水主要流向为自北向南,核部局部存在由东槽谷向西槽谷的跨核部径流,根据模拟情况来看,东西槽谷普遍存在水头差,东侧槽谷水位一般高于西侧槽谷水位,在槽谷两侧发育的溪沟为局部排泄基准面,花溪河为区域内排泄基准面,地下水水位相对较低。

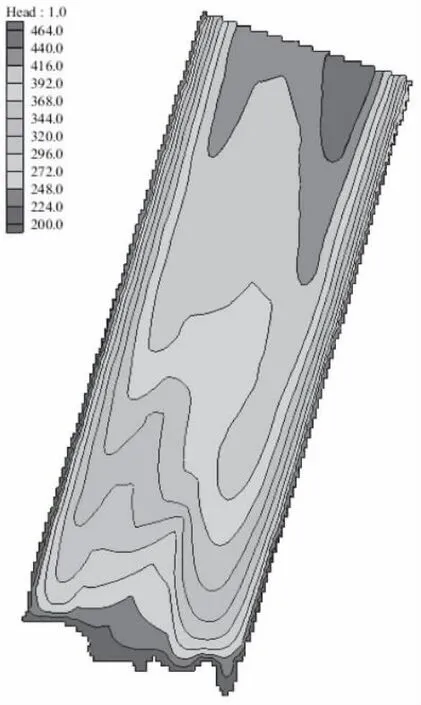
图4 隧址区天然状态下渗流场Fig.4 Natural seepage field in the tunnel site area

3.1.2隧道开挖过程中渗流场模拟

考虑到隧道的实际长度,设定隧道施工工期为2年,分为8个应力期,将每个应力期分3个时间步长,每个时间步长为30 d。两端同时掘进,模拟隧道开挖后到结束时地下水渗流场的变化。隧道概化为Drain边界导入模型,综合水力传导系数根据地层境况赋值。隧道开挖一年后,两翼地下水水位已明显受到隧道开挖的影响,局部地区已经开始形成地下水位降落漏斗,如图5(a)所示。隧道开挖两年后,隧道完全贯通,以隧道中线为中心形成影响范围较大的地下水位降落漏斗;隧道附近地下水水位下降明显,形成了以隧道为排泄基准的新的补径排系统,如图5(b)所示。

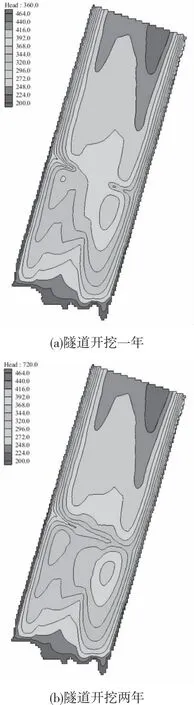
图5 隧道施工阶段渗流场变化图Fig.5 Diagram of seepage field changes during tunnel construction stage

与天然状况下渗流场相比,随着开挖时间的增加,以隧道开挖面为中心形成的降落漏斗影响范围逐渐增加,在开挖一年时,由于掘进段主要为非可溶岩,所以影响半径较小,背斜核部地下水水位变化较小;开挖一年过后,掘进到隧址区主要含水层为雷口坡和嘉陵江地层(T1j+T2l)灰岩,所以以隧道开挖面为中心,形成了影响范围较大的降落漏斗,开挖的隧道成为了局部的排泄基准面,而背斜核部地下水水位亦有下降;隧道贯通后,此时隧道段已成为了局部排泄基准,原本由北自南的地下水流动方向,已变成以隧道为中心汇流,背斜核部区域地下水水位进一步下降,降落漏斗影响范围分布并不对称,西侧大于东侧,这与两侧隧道高程有关,隧道西侧进口隧道高程为252.1 m,东侧进口隧道高程为336.3 m,所以隧道西侧影响范围大于东侧。

3.1.3隧道运营期地下水环境恢复模拟

分析隧道在进行有效的堵水措施之后隧址区地下水的恢复状况。如图6(a)所示,隧道运营五年后,隧址区地下水的恢复情况较好,水位已明显恢复,隧道右侧地下水恢复速度明显大于左侧,这与右侧隧道埋深相对更浅有关;如图6(b)所示,隧道运营十年后水位已趋于稳定,隧道右侧地下水基本恢复至天然状态下水位,但隧道左侧地下水已难以恢复到天然状态下水位。主要原因是隧道开挖改变了地下水循环系统,同时使得地表水径流也受到影响,最终造成地下水位难以恢复到天然状态,而隧道右侧相对埋深较浅,影响较小。

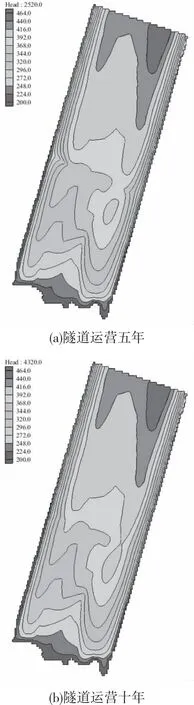
图6 隧道运营阶段渗流场变化图Fig.6 Changes in seepage field during tunnel operation stage

3.2 隧道工程因素对地下水环境影响规律

3.2.1隧道高程对地下水环境影响分析

如图7所示,随着隧道高程的增加,地下水降落漏斗的影响半径减小,最大降深也随之减少。隧道高程为250 m时,地下水环境变化最为明显,地下水水位急剧下降,在隧道中线形成了较大的降落漏斗,水位降深也非常明显,最大降深达92 m,影响半径约为1.8 km;即使在运营期进行堵水措施后地下水也很难恢复至天然状态;隧道高程为350 m时,地下水位略微变化,隧道开挖对地下水环境的影响十分局限,最大降深为16 m,影响半径约为1 km;在进行有效堵水后,地下水位能完全恢复至天然状态。隧道高程增加100 m,即隧道相对埋深减少100 m,最大降深减少了76 m,影响半径减少了约0.8 km。由此可见,隧道位于地下水位以下时,为了降低隧道修建过程中对地下水环境和施工安全的影响,应当尽量浅埋。

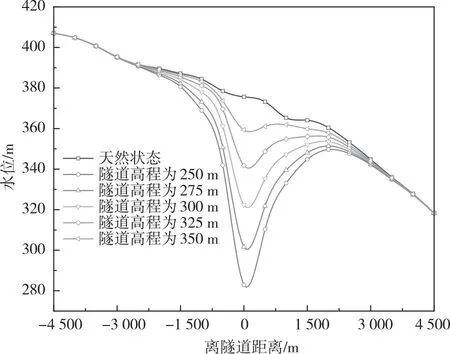
图7 地下水位沿隧道段随高程变化剖面图Fig.7 Profile of groundwater level changes with elevation along the tunnel section

3.2.2隧道水力传导系数对地下水环境影响分析

软件GMS中用水力传导系数C表示含水层与隧道之间水量流动的效率,可以用以下表达式来描述[18]:

C=KLW/M

(1)

式中:K为渗透系数,m/d;M为隧道底部弱透含水层的厚度,m;L为隧道的长度,m;W为隧道的宽度,m。

隧道的水力传导系数是根据地层境况进行赋值的,隧道两侧的水力传导系数较小,改变两侧水力传导系数,地下水环境变化并不明显,因此,仅改变隧道核部地区水力传导系数。在不改变其它参数的情况下,设定隧道高程为250 m,模拟水力传导系数分别为0.8、0.6、0.4、0.2的地下水环境变化情况。如图8所示,随着水力传导系数的减小,地下水水位上升,影响范围减小。水力传导系数C由0.8变化到0.2,最大降深从92 m减小到了46 m,影响半径从1.8 km减小到1.4 km。水力传导系数减小到原来的1/4,最大降深减小了一半,影响半径减小了0.4 km。隧道水力传导系数是一个由多因素综合确定的系数。在隧道的长度、宽度、弱透含水层的厚度确定的情况下,一定程度上能反应隧道穿越不同含水岩组对地下水环境的影响。所以在隧道由弱透水性岩组掘进至强透水性岩组,应更加注意防水,避免突水危害。

图8 地下水位沿隧道段随水力传导系数剖面图Fig.8 Profile of groundwater level along the tunnel section with hydraulic conductivity coefficient

4 鹿角隧道涌水量预测

工程中常用大气降雨入渗法和地下水径流模数法对涌水量进行预测,但因为拟建鹿角隧道穿过含水体时全部从地下水位以下通过,穿越水平径流带,故不采用大气降雨入渗法计算隧道涌水量。本节采用地下水径流模数法和数值模拟法两种方法对鹿角隧道的最大涌水量进行分段预测,并对结果进行对比分析,根据隧道途经的地层岩性、构造不同,将隧道分为7段,分别以段为单位进行涌水量计算。

4.1 地下水径流模数法

采用地下水径流模数法进行涌水量计算时,计算精度主要取决于地下水径流模数和地表流域范围取值。应结合不同的水文地质情况,确定合适的地表流域区与地下水径流模数,其计算公式如下[19]:

Q=86.4MA

(2)

式中,Q为隧道日正常涌水量,m3/d;M为地下水径流模数,L/s·km2;此处M值确定主要根据1∶20万重庆幅水文地质报告;A为隧道通过含水体地段的集水面积,km2;86.4为单位换算系数。计算结果见表3。

表3 涌水量计算结果Tab.3 Calculation results of water inflow

4.2 数值模拟法

根据所建模型和隧道通过地层岩性,将模型按里程分为七个分区并赋予分区代号。通过GMS中的Flow budget模块读取隧道各分段涌水量,隧道贯通时,即涌水量到达最大,此时模型中各个分区中排水沟的排水量就是最大涌水量,结果如表3所示。

4.3 隧道涌水量预测

由表3可知,运用地下水径流模数法计算涌水量时,由于核部地区的飞仙关地层在地表未出露,地下水径流模数法的涌水量预测结果不包括飞仙关地层的涌水量,最大涌水量合计为27 524.89 m3/d,在YK4+900—YK5+455和YK5+87—YK6+685的涌水量分别达到了10 324.8 m3/d和15 465.6 m3/d,约占整体涌水量的90%。当运用数值模拟的方法去计算涌水量时,在不考虑YK5+455—YK5+875这段里程的涌水量的情况下,两种方法算出的涌水量非常接近,且两种方法所计算的涌水量变化趋势大致相同。

在采用地下水径流模数法计算涌水量时,由于飞仙关地层在地表未出露,无法计算这一部分的涌水量,因此计算得到的最大涌水量低估了实际涌水量;而用数值模拟法计算涌水量时,由于在进行参数分区时,将核部地区的渗透系数和给水度概化为了一个参数,而实际情况是飞仙关组地层作为弱含水层其计算参数应小于概化值,所以数值模拟法计算的最大涌水量高估了实际涌水量。综上所述,估测隧道实际最大涌水量介于27 524.89 m3/d～36 086.72 m3/d之间。