基于相关分析和带遗忘因子的随机梯度的非线性系统Wiener模型辨识

丁振宇 李峰 徐亮亮

文章編号：2096-398X2024）03-0197-06

（1.江苏理工学院 电气信息工程学院， 江苏 常州 213001； 2.常州铁道高等职业技术学校， 江苏 常州 213011）

摘 要：实际工业过程往往呈现强非线性和时滞特性，在复杂工况下如何建立过程的高精度模型并对其进行有效控制是研究重点.本文研究了一种基于相关分析的非线性系统Wiener模型辨识.Wiener非线性模型由动态线性子系统和静态非线性子系统串联组成，利用时滞状态空间模型和神经模糊模型分别建立动态线性子系统和静态非线性子系统，并利用设计的组合信号实现Wiener非线性模型分离辨识.首先，利用后移算子的性质，将时滞状态空间模型转化为传递函数模型，在高斯信号作用下利用相关分析方法辨识动态线性子系统的参数，解决了Wiener模型中间变量不可测问题.其次，为了改善辨识模型的精度和收敛速度，推导了带遗忘因子的递推随机梯度方法，得到静态非线性子系统的参数估计.将提出的非线性Wiener模型辨识方法运用于连续搅拌反应釜，实验仿真结果表明，本文提出的Wiener模型辨识方法能够有效辨识连续搅拌反应釜系统，并取得较好的控制效果.

关键词：非线性系统； Wiener模型； 神经模糊模型； 相关分析

中图分类号：TP273    文献标志码： A

Identification of Wiener model for nonlinear systems based on correlation analysis and stochastic gradient with forgetting factor

DING hen-yu1，  LI Feng1*， XU Liang-liang2

1.College of Electrical and Information Engineering， Jiangsu University of Technology， Changzhou 213001， China; 2.Changzhou Railway Higher Vocational and Technical School， Changzhou 213011， China）

Abstract：The actual industrial process often presents strong nonlinearity and strong coupling in operation.How to control the system quickly and accurately under complex working conditions is a current research focus.In this paper，an identification of Wiener model for nonlinear systems based on correlation analysis is studied.The Wiener nonlinear model consists of a dynamic linear subsystem and a static nonlinear subsystem in series，and the dynamic linear subsystem and the static nonlinear subsystem are established by using time-delay state space model and neural fuzzy model respectively，and the Wiener nonlinear model is separated and identified by using the designed combined signal.Firstly，the time-delay state space model is transformed into a transfer function model by using the properties of the backward operator，and the parameters of the dynamic linear subsystem are identified by correlation analysis method under the action of Gaussian signal，which solves the unmeasurable problem of intermediate variables in Wiener model.Secondly，in order to improve the accuracy and convergence speed of the identification model，a recursive stochastic gradient method with forgetting factor is derived to estimate the parameters of the static nonlinear subsystem.The proposed nonlinear Wiener model identification method is applied to continuous stirred tank reactor.The simulation results show that the proposed Wiener model identification method can effectively identify the continuous stirred tank reactor system and achieve better control effect.

Key words：nonlinear system； Wiener model； neuro-fuzzy model； correlation analysis

0 引言

现代生产过程正向大规模、连续化、集成化方向发展，呈现强非线性、时滞、多模态以及不确定性等复杂特性，这些因素导致难以建立精确的数学模型.在实际生产过程建模研究中，物理系统建模［1-3］和数据驱动建模［4-6］已成为两种主流建模方法.物理系统建模是利用实际过程的物理特征进行建模，需要知道实际过程的知识，而且由于实际生产系统的复杂性和不确定性，因此难以建立高精度的机理模型［7］.数据驱动建模不需要深入的过程知识，因此受到了广泛关注［8］.目前应用较为广泛的数据驱动模型结构有Volterra级数［9］、神经网络［10］、支持向量机［11］、马尔可夫跳跃系统［12］以及块结构非线性模型等［13］.

陕西科技大学学报第42卷

第3期丁振宇等：基于相关分析和带遗忘因子的随机梯度的非线性系统Wiener模型辨识

在诸如化学过程、生物和生理系统等采用较普遍的是块结构模型［14］.根据模块的具体连接形式，块结构模型可以分为：Hammerstein模型、Wiener模型、以及其组合形式Hammerstein-Wiener模型和Wiener-Hammerstein模型.Wiener模型作为典型的非线性动态系统，在工业生产过程中有着广泛的应用，如pH中和过程［15］、连续搅拌反应釜［16］、蒸馏塔［17］以及three-tank模型［18］等，因此本文主要探讨Wiener模型的辨识问题.

Wiener模型由一个动态线性子系统和一个静态非线性子系统串联而成，通常用来描述在输出部分存在非线性元素的系统.近年来，Wiener模型的参数估计问题在系统辨识领域越来越得到关注.针对一类非线性Wiener时不变系统，Dong等［19］提出了一种带遗忘因子的递推最小二乘算法，改善了参数辨识精度.考虑到Wiener系统辨识的过参数和最小二乘精度低的問题，文献［20］提出了一种基于分解技术的多新息最小二乘辨识方案.针对传统粒子群优化算法无法解决新息向量包含中间不可测变量的问题，文献［21］结合关键项原理，采用启发式粒子群算法辨识Wiener模型参数.在各类实际生产中，由于信号在采集、传输和接收等过程都需要消耗一定的时间，导致系统的输出和输入之间往往会产生时间上的延迟，即时滞现象［22］.这种现象对系统参数辨识存在一定的影响，因此在系统辨识中考虑时滞对系统的影响至关重要.针对具有时滞的非线性系统，Atitallah等［23］将时滞项归入Wiener模型的线性子系统中，在此基础上利用基于递推最小二乘的优化技术解决参数辨识问题.文献［24］提出了一种基于递阶梯度的算法，同时辨识线性和非线性子系统的参数以及Wiener模型的时滞.上述提到的各类方法有效解决了Wiener模型的参数辨识问题，但是研究中都利用多项式拟合Wiener模型的非线性子系统，在拟合复杂不连续非线性函数时，随着多项式阶次增加其逼近能力达到饱和.此外，在辨识过程中设置非线性模块的首项参数为1，在此条件下分离出线性和非线性模块的参数值，降低了模型辨识精度，且具有一定的局限性.

针对上述问题，本文提出了一种基于神经模糊Wiener模型的非线性系统辨识方法.首先，利用带时滞的状态空间模型和神经模糊网络模型分别建立Wiener模型的动态线性子系统和静态非线性子系统.其次，根据可分离信号在静态非线性系统下的相关函数特性设计组合信号，解决了Wiener模型中间变量信息不可测问题.此外，基于组合信号的输入输出数据，利用相关性分析法和带遗忘因子的递推随机梯度方法分别辨识Wiener模型的动态线性子系统和静态非线性子系统，实现参数分离辨识.最后，将提出的辨识方法用于CSTR过程的控制.

1 含输出噪声干扰的Wiener模型

图1显示了一类输出噪声干扰的Wiener模型，其中动态线性子系统和静态非线性子系统分别利用时滞状态空间模型和神经模糊网络模型建立.

根据图1，Wiener模型的输入/输出数学表达式为：

xk+1）=Axk）+Bxk－1）+huk）

vk）=cxk）

yk）=fvk））+ek）（1）

式（1）中：xk）是状态变量，A∈Rn×n，B∈Rn×n，h∈Rn×1以及c∈R1×n是状态空间模型的参数矩阵或向量，vk）为中间不可测变量，ek）代表白噪声，f·）表示静态非线性子系统.

根据单位后移算子的性质，可以将时滞状态空间模型转换成传递函数模型，基于文献［25］的研究，得到如下引理.

引理1 对于图1所示的时滞状态空间模型，动态线性子系统的输入输出关系可以用式（2）描述：

vk）=cz2I－Az－B）－1hzuk）=z－2ncadj［z2I－Az－B］hzz－2ndet［z2I－Az－B］uk）=bz）az）uk）（2）

式（2）中：az）=z－2ndet［z2I－Az－B］=1+a1z－1+…+a2nz－2n，bz）=z－2n+1cadj［z2I－Az－B］h=b1z－1+…+a2n－1z－2n－1）.

根据图1和上述结论，本文提出的Wiener模型的输入输出关系可以被表述为：

vk）=bz）az）uk）（3）

yk）=fvk））+ek）（4）

式（3）、（4）中：f·）表示静态非线性子系统，vk）代表中间不可测变量，az）=1+a1z－1+…+anaz－na，bz）=b1z－1+…+bnbz－nb，na和nb都是模型的阶次.

本文采用神经模糊网络拟合Wiener模型的静态非线性子系统，结构如图1所示，因此：

ηk）=fvk））=∑Ll=1φlvk））wl（5）

式（5）中：φlvk））=μlvk））∑Ll=1μlvk）），μlvk））=exp－vk）－cl）2σ2l，cl和σl分别是隶属度函数的中心和宽度，wl表示权重，L是模糊规则数.

对于给定的ε，Wiener模型的参数要满足下述条件：

E[Af^][Av^]k），[Aa^]z），[Ab^]z）=12N∑Nk=1[JByk）－[Ay^]k）]2≤εs.t.

[Av^]k）=[Ab^]z）[Aa^]z）uk）[Aη^]k）=[Af^][Av^]k））[Ay^]k）=[Aη^]k）+ek）（6）

式（6）中：ε表示给定的阈值，N是输入输出数据的数目，符号^表示估计.

2 基于Wiener模型的两阶段系统辨识

根据前期的研究可以得知，如果输入信号是满足uk）～0， σ2u）的高斯信号，动态线性子系统的输出是方差不同的高斯信号，满足可分离信号的特征，能够实现动态线性子系统L·）和静态非线性子系统f·）参数的分离辨识［26］，本文将组合式信号拓展到Wiener模型CSTR系统模型中，利用可分离输入信号及其输出辨识动态线性子系统.

引理2 对于式（1）中描述的Wiener模型，如果输入信号是零均值的可分离信号，那么存在一个常数使得如下关系成立：

Ryuτ）=b0Gq）Ruτ）（7）

式（7）中：R·）表示相关函数，Ryuτ）=Eyk）uk－τ）），Ruτ）=Euk）uk－τ）），b0=Eyk）vk））Evk）vk）），Gz）=bz）az）=b1z－1+b2z－2+…+bnbz－nb1+a1z－1+a2z－2+…+anaz－na.

关于引理2的证明可以参考前期的研究［26］，本文省略证明.

2.1 动态线性子系统辨识

将式（7）展开可知：

Ryuτ）=－∑nai=1aiRyuτ－i）+b0∑nbj=1bjRuτ－j）（8）

令bj=b0bj，可得：

Ryuτ）=－∑nai=1aiRyuτ－i）+∑nbj=1bjRuτ－j）（9）

利用相關性分析法辨识动态线性子系统的参数，设τ=1，2，…，PP≥na+nb），则：

[Aθ^]=RψTψψT－1（10）

式（10）中：[Aθ^]=[Aa^]1，[Aa^]2，…，[Aa^]na，[Ab^]1，[Ab^]2，…，[Ab^]nb]，R=[JBRyu1），Ryu2），…，RyuP）]，

ψ=－Ryu0）－Ryu1）…－RyuP－1）0－Ryu0）…－RyuP－2）00…－RyuP－na）

Ru0）Ru1）…RuP－1）0Ru0）…RuP－2）00…RuP－nb）].

这里用式（11）计算Ryuτ）和Ruτ）：

Ryuτ）=1N∑Nk=1yk）uk－τ）Ruτ）=1N∑Nk=1uk）uk－τ）（11）

2.2 静态非线性子系统辨识

本文采用四层神经模糊模型拟合Wiener模型的静态非线性子系统［27］，首先基于动态线性子系统辨识得到的参数得到中间变量的估计值[Av^]，并利用聚类算法［28］估计神经模糊模型的中心cl和宽度σl，根据式（4）和式（5）可以将神经模糊Wiener模型的输出表示为：

yk）=∑Ll=1φlvk））wl+ek）（12）

式（12）可以简化为：

yk）=φTk）+ek）（13）

式（13）中：

φk）=［φ1vk），φ2vk），…，φLvk））］T∈RL，=［w1，w2，…，wL］T∈RL.

定义如下准则函数：

J=∑Nk=1［yk）－φTk）[A^]］2（14）

极小化准则函数，利用随机梯度算法可以得到静态非线性子系统的参数估计.为了提高参数辨识精度和收敛速度，在递推随机梯度算法中引入遗忘因子，推导了如下带遗忘因子的递推随机梯度方法：

[A^]k）=[A^]k－1）+[Aφ^]k）rk）[JByk）－[Aφ^]k）[A^]k－1）]（15）

rk）=rk－1）σ+‖[Aφ^]k）‖2（16）

[Aφ^]k）=［φ1[Av^]k），φ2[Av^]k），…，φL[Av^]k））］T（17）

[A^]k）=［w1，w2，…，wL］T∈RL（18）

综上所述，基于神经模糊Wiener模型的非线性模型的辨识方法概括为如下步骤：

Step 1 将时滞状态空间模型转换成传递函数模型，基于可分离信号的输入/输出数据，利用相关性分析法辨识线性子系统的参数.

Step 2 在随机信号作用下，利用聚类算法计算隶属度函数的cl和宽度σl.

Step 3 将随机信号及其产生的输出分别作为Wiener模型的输入和输出，利用带遗忘因子的递推随机梯度方法估计非线性子系统参数.

3 仿真结果与分析

本文选取了一个连续搅拌反应釜（Continuous Stirred Tank Reactor， CSTR）过程作为研究对象［29］，其反应在恒温反应器中进行.在CSTR的动力学方程中，浓度CA对时间的导数表示非线性系统，浓度CB对时间的导数表示线性系统.反应的流程示意图和变量初值如图2和表1所示.该反应的过程可以量化为式（19）和式（20）.

dCAdt=－k1CA－k3C2A+FVCAf－CA）（19）

dCBdt=k1CA－k2CB+FVCB（20）

式（19）、（20）中：CA和CB分别是物质A、B的浓度，F表示流速，CAf是物质A的进料浓度，V是反应器的体积，k1，k2和k3为动力学参数.

利用满足N0， 1）的高斯信号和幅值在［-1，1］区间内的随机信号构成的组合式信号源，定义噪信比δns=varek）/varηk）×100%，对系统的输出加上3.42%的白噪声干扰，并使用u=F－34.3）/34.3和y=CB－1.12）/1.12归一化系统的输入输出，部分输入输出信号图如图3所示.

图3 组合信号的部分输入输出

首先，利用相关性分析法辨识Wiener模型的动态线性子系统参数，辨识结果为：

a=［a1，a2，a3，a4］=  ［0.936 4，0.333 1，0.356 5，0.001 7］

b=［b1，b2，b3］=  ［－0.038 5，0.037 4，0.036 0］

因此，动态线性子系统的输入输出关系可以写成：

vk）=bz）az）uk）

az）=1+0.936 4z－1+0.333 1z－2－0.356 5z－3－0.001 7z－4

bz）=－0.038 5z－1+0.037 4z－2+0.036 0z－3

其次，設置参数S0=0.999，ρ=1.0，λ=0.02，σ=0.9，利用聚类的带遗忘因子的随机梯度方法辨识神经模糊模型的中心cl，宽度σl和权重wl.

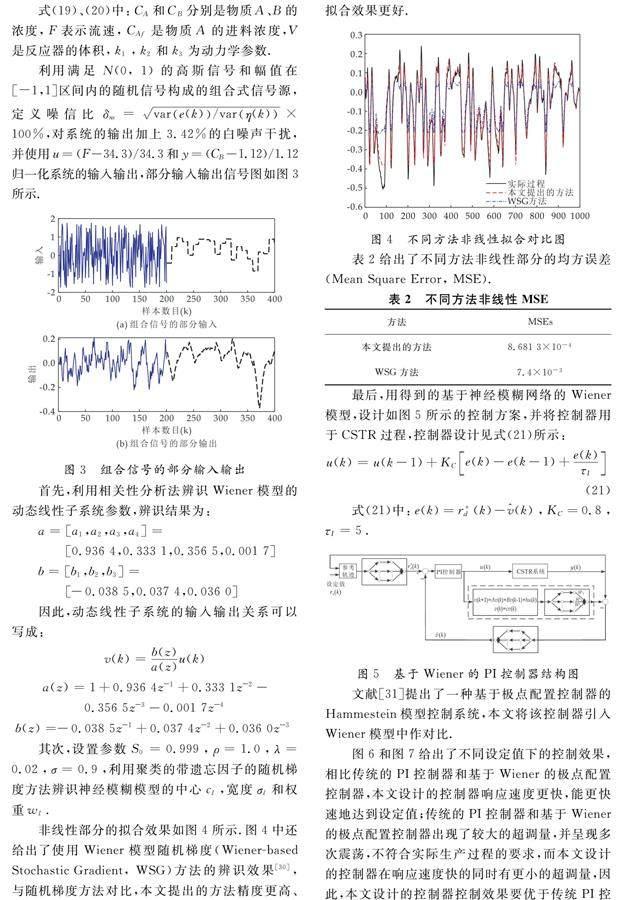
非线性部分的拟合效果如图4所示.图4中还给出了使用Wiener模型随机梯度（Wiener-based Stochastic Gradient， WSG）方法的辨识效果［30］，与随机梯度方法对比，本文提出的方法精度更高、拟合效果更好.

最后，用得到的基于神经模糊网络的Wiener模型，设计如图5所示的控制方案，并将控制器用于CSTR过程，控制器设计见式（21）所示：

uk）=uk－1）+C[JBek）－ek－1）+ek）τI]（21）

式（21）中：ek）=r*dk）－[Av^]k），C=0.8，τI=5.

文献［31］提出了一种基于极点配置控制器的Hammestein模型控制系统，本文将该控制器引入Wiener模型中作对比.

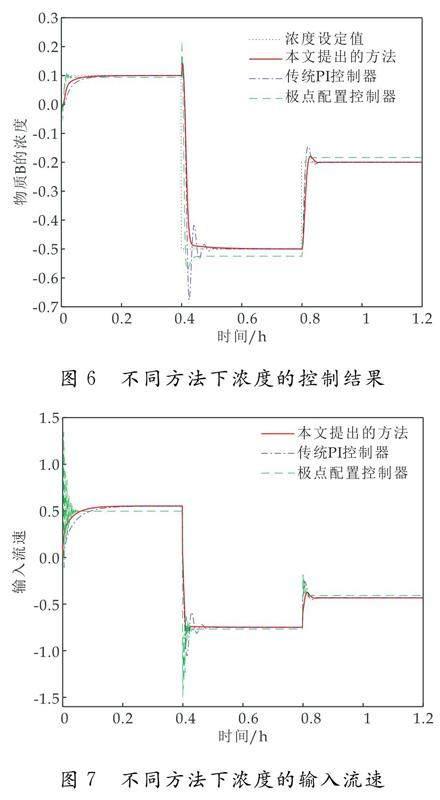
图6和图7给出了不同设定值下的控制效果，相比传统的PI控制器和基于Wiener的极点配置控制器，本文设计的控制器响应速度更快，能更快速地达到设定值；传统的PI控制器和基于Wiener的极点配置控制器出现了较大的超调量，并呈现多次震荡，不符合实际生产过程的要求，而本文设计的控制器在响应速度快的同时有更小的超调量，因此，本文设计的控制器控制效果要优于传统PI控制器和基于Wiener的极点配置控制器.

4 结论

本文提出了一种基于相关分析的非线性系统Wiener模型辨识，能够对复杂非线性系统进行有效辨识和控制.利用高斯信号和随机信号设计组合式信号，利用神经模糊Wiener模型建立具有分离辨识特征的复杂非线性动态系统模型，运用提出的两阶段辨识方法辨识神经模糊Wiener模型.仿真实验结果表明，提出的基于神经模糊Wiener模型非线性系统辨识方法比WSG方法的辨识方法精度更高，同时本文设计的控制器效果也比传统的PI控制器和基于Wiener的极点配置控制器好.因此提出的方法能够有效对复杂非线性系统进行辨识和控制.

参考文献

［1］ 严康为，龙鑫林，鲁军勇，等.高倍率磷酸铁锂电池简化机理建模与放电特性分析.电工技术学报，2022，373）：599-609.

［2］ 尚群立，李梦强，张晶瑜.气动截止阀机理建模及其在阀门故障诊断中的应用.浙江工业大学学报，2020，482）：154-158，216.

［3］ 邓晓刚，于佐军.连续搅拌反应釜机理建模与开放式虚拟仿真系统开发.实验技术与管理，2016，331）：114-117，121.

［4］ 董世建，孟 振，时侠圣，等.雕刻机系统数据驱动建模与容错跟踪控制．控制与决策，2023，389）：2 569-2 577.

［5］ 徐巧菲，黄景涛，郭喜风，等.基于偏互信息过热器温差数据驱动建模研究.控制工程，2019，2612）：2205-2210.

［6］ 蔡昌春，息梦蕊，刘昊林，等.基于数据驱动和多场景技术的微电网并网等效建模.电力自动化设备，2022，429）：64-69.

［7］ 陈 诚，黄 剑，刘 磊，等.基于数据驱动的气动柔性关节Takagi-Sugeno模糊系统建模与预测控制.控制理论与应用，2022，394）：633-642.

［8］ 孔祥玉，王晓兵，罗家宇，等.基于动态高效潜结构投影的质量相关故障检测.控制理论与应用，2021，3812）：2 076-2 084.

［9］ Shi Y，Yu D L，Tian Y，et al.Modified volterra model based non-linear model predictive control of IC engines with real-time simulations.Transactions of the Institute of Measurement and Control，2015，392）：208-223.

［10］ Liang Y，Xu S，Hong ，et al.Neural network modeling and single-neuron proportional-integral-derivative control for hysteresis in piezoelectric actuators＼[J＼].Measurement and Contro，2019，529-10）：1 362-1 370.

［11］ Liu X，hang .Earth pressure balance control of shield tunneling machine based on nonlinear least squares support vector machine model predictive control.Measurement and Control，2018，521-2）：3-10.

［12］ hao Y J，Fatehi A，Huang B.A data-driven hybrid ARX and Markov-chain modeling approach to process identification with time varying time delays.IEEE Transactions On Industrial Electronics，2017，645）：4 226-4 236.

［13］ Liang Y，Xu S，Hong ，et al.Neural network modeling and single-neuron proportional-integral-derivative control for hysteresis in piezoelectric actuators.Measurement and Control，2019，529-10）：1 362-1 370.

［14］ 仲国民，孙明轩.一类Wiener非线性时变系统的迭代学习辨识.电子与信息学报，2021，439）：2 594-2 600.

［15］ Wang Q C，hang J .Wiener model identification and nonlinear model predictive control of a pH neutralization process based on Laguerre filters and least squares support vector machines.Frontiers of Information Technology & Electronic Engineering，2011，121）：25-35.

［16］ Yuan P，hang B，Mao  .A self-tuning control method for Wiener nonlinear systems and its application to process control problems.Chinese Journal of Chemical Engineering，2017，25：193-201.

［17］ Bloemen H H J，Chou C T，Van Den Boom T J J，et al.Wiener model identification and predictive control for dual composition control of a distillation column.Journal of Process Control，2001，11：601-620.

［18］ 景绍学，李正明.Wiener系統的变聚点样条逼近递推贝叶斯算法.控制理论与应用，2017，341）：13-21.

［19］ Dong S J，Yu L，hang W A，et al.Robust hierarchical identification of wiener systems in the presence of dynamic disturbances.Journal of the Franklin Institute，2020，3576）：3 809-3 834.

［20］ 韩琛晔.基于多新息算法的阶次未知的Wiener系统参数估计． 河南理工大学学报自然科学版），2021，401）：118-124.

［21］ Sersour L，Djamah T，Bettayeb M.Fractional Wiener system identification using heuristic optimization technique based on key_term principle.IFAC-Papers OnLine，2019，5213）：189-193.

［22］ 孙 赫，王稳稳，周国振，等.带不同时滞的单通道ARMA信号加权融合反卷积Wiener滤波器.现代信息科技，2022，63）：54-57.

［23］ Atitallah A，Bedoui S，Abderrahim .Joint parameter and time-delay identification algorithm and its convergence analysis for Wiener time-delay systems.Circuits，Systems，and Signal Processing，2020，39：199-222.

［24］ Atitallah A，Bedoui S，Abderrahim .Identification of wiener time delay systems based on hierarchical gradient approach.IFAC-PapersOnLine，2015，481）：403-408.

［25］ Gu Y，Ding F.Auxiliary model based least squares identification method for a state space model with a unit time-delay.Applied Mathematical Modelling，2012，36：5 773-5 779．

［26］ Jia L，Xiong Q，Li F.Correlation analysis method based SISO neuro-fuzzy wiener model.Journal of Process Control，2017，58：73-89．

［27］ 李 峰，罗印升，李 博，等.基于组合式信号源的Hammerstein-Wiener模型辨识方法.控制与决策，2022，3711）：2 959-2 967.

［28］ Li F，heng T，He N B，et al.Data-driven hybrid neural fuzzy network and ARX modeling approach to practical industrial process identification.IEEE/CAA Journal of Automatica Sinica，2022，99）：1 702-1 705.

［29］ Li F，hu X J，He N B，et al.Parameter learning for the nonlinear system described by hammerstein model with output disturbance.Asian Journal of Control，2023，252）：886-898.

［30］ hou L C，Li X L，Pan F.Gradient based iterative parameter identification for wiener nonlinear systems.Applied Mathematical Modelling，2013，37：8 203-8 209.

［31］ Hong X，Chen S.The system identification and control of hammerstein system using non-uniform rational B-spline neural network and particle swarm optimization.Neurocomputing，2012，82：216-223.

【責任编辑：蒋亚儒】

基金项目：国家自然科学基金项目（62003151）； 江苏省常州市科技计划项目（CJ20220065，CM20223015）； 江苏省研究生科研与实践创新项目（SJCX22_1477）

作者简介：丁振宇2000—），男，江苏宿迁人，在读硕士研究生，研究方向：块结构模型辨识

通讯作者：李 峰1987—），男，江苏淮安人，副教授，博士，研究方向：数据驱动的复杂非线性动态模型化，lifeng@jsut.edu.cn