信息科技课程中计算思维多层进阶式目标体系设计

冯友梅 王昕怡 温佳 王壮伟 颜士刚

基金项目：全国教育科学规划2022年度教育部重点项目“本土计算思维描述框架及评价体系设计研究”（项目编号：DCA220445）

[摘   要] 计算思维是重要的信息科技学科核心素养，但面向计算思维的结构化教学体系尚未形成。经分析，计算思维目标体系的缺失是其直接原因。鉴于此，文章以“知识与思维内在统一”为基本立场，将计算思维转换为与其内在统一的知识结构——计算思维二维描述框架，并设计知识结构水平的判断标准——知识结构九水平分类体系。在此基础上，给出二者相结合的计算思维目标体系设计方案并结合实例详解：首先，将计算思维二维描述框架中的要素逐层分解以保证各教学单位均有其聚焦的计算思维要素；而后，以知识结构九水平分类体系为依据，形成纵向上层层细化、横向上计算思维（知识）结构水平不断提升的计算思维多层进阶式目标体系。该目标体系设计方案可结束信息科技课程内容教学与计算思维教学两条线的尴尬局面，使计算思维在与课程内容融合统一的教学路径中真正落地。

[关键词] 信息科技课程； 计算思维； 目标体系； 多层进阶式； 知识结构九水平分类体系

[中图分类号] G434            [文献标志码] A

[作者简介] 冯友梅（1983—），女，河北香河人。副教授，博士，主要从事信息技术课程与教学、思维可视化理论与实践研究。E-mail：youmeifeng2008@163.com。王壮伟为通讯作者，E-mail：wzhw0511@163.com。

一、引   言

作为核心素养落地的重要抓手，大单元教学在基础教育领域备受推崇。其核心要义为，通过将作为“独木”的课汇聚为作为“林”的单元，实现集中力量培养核心素养的教育目标。信息科技学科亦践行此思路。作为信息科技学科聚焦的重要核心素養和学科立足之本[1]，计算思维的培养路径当然也不例外。事实上，计算思维的有效培养，需要将课程作为整体集中发力。所谓集中发力，即要求在将课程汇聚为单元之后，各单元也要形成以计算思维发展脉络为内在线索的、环环相扣的单元群。然而，截至目前，此种意义上的单元群尚未形成。换言之，在既有的所谓单元群（如各版本高中信息技术教材中呈现的单元群）中，很难找到计算思维的清晰进阶脉络，单元之间并未形成面向计算思维的合力。如此，从计算思维培养的角度看，单元便沦为新的“独木”，学科依然未解决“独木不成林”的痼疾。事实上，如何使计算思维培养系统化、结构化，亦是广大信息科技教研员及一线教师倍感迷茫的问题。

鉴于此，本文深入分析信息科技课程中计算思维培养难成体系的原因——计算思维目标体系难以形成。在此基础上，以“知识与思维内在统一”为基本立场，给出计算思维多层进阶式目标体系的设计方案并结合实例详解。借此为计算思维在信息科技学科稳妥落地提供真正可行且可被一线直接参照的思路和样本。

二、面向计算思维的结构化教学体系

缘何难以形成

众所周知，教学目标是教学实践的重要线索和依据。从计算思维培养的角度来看，信息科技课程各教学单元间的“貌合神离”，正是缘于可将众单元“黏合”成整体结构的计算思维目标体系的缺失。

对于计算思维单元目标设计，目前主要有以下三种方式：其一，在课程标准的“内容标准”中选取内容作为计算思维单元目标。如将计算思维单元目标确定为“描述人工智能的基本特征，利用开源软硬件平台设计搭建简单智能系统”[2]。其二，将课程标准规定的计算思维学段目标（水平）作为单元目标。如将计算思维单元目标确定为“根据给定的任务进行需求分析，明确需要解决的关键问题”[3]。其三，将计算思维完整过程作为单元目标。如将计算思维单元目标确定为“通过经历抽象、分解、算法设计、应用、评估、总结、迁移这一过程解决复杂问题”[4]。

以上三种计算思维单元目标设计方法中，第一种的问题最为突出，表现为单元目标与学段目标指向不一致，即计算思维单元目标与学段目标间无直接、明朗的关系，此为方向性错误。第二种及第三种目标设计方法虽错不至此，但依然存在问题，即不同单元“共享”相同的计算思维目标。此问题在第三种目标设计方法中表现更甚：只要涉及计算思维目标，均用前文所示计算思维过程表示。结果是，看似每个单元均对计算思维的发展有所贡献，但无法清晰说明具体贡献是什么，即无法明确每个单元究竟在何种程度上促进了计算思维的发展。虽然以上三种目标设计方法存在的问题不同，但均导致了相同的结果：从计算思维培养的角度看，各单元之间仅是无清晰逻辑关联的线性排列，与结构化教学体系相去甚远。事实上，在第二种及第三种目标设计方法中，各单元之所以需“共享”同一计算思维目标，主要原因为目标的跨层使用，即用少量、抽象的学段甚至课程层面的计算思维目标指导大量、具体的单元层面的教学实践。当然，很多研究者已经认识到目标跨层使用的不合理性，并尝试将宏观计算思维目标细化为多层关联的目标体系，所做工作集中于对计算思维过程中内含的各要素或环节（“抽象”“算法设计”等）进行分解。例如，将“抽象”细化为“删除”“过滤”“提取”“符号化”四个要素[5]等等。然而，无论采用何种思路，均无法分解出足够多的计算思维“过程”要素，以支持为各个层面（包括单元层面）教学实践提供明确计算思维目标的“金字塔结构”目标体系的形成。

计算思维目标体系的缺失，便意味着单元间无清晰的计算思维内在进阶线索。结果便是，从计算思维培养的角度，信息科技课程各教学单元各自为政、形同散沙，难以形成面向计算思维的合力。进一步，单元无具体明确的计算思维目标，便无法有效开展计算思维单元评价，面向计算思维的“教—学—评”一体化也会落空。长此以往，计算思维很有可能沦落为“一个什么都能装的筐”。

三、计算思维目标体系设计基础及宏观思路

除了计算思维所属的学科核心素养，信息科技课程还有另一个核心范畴——学科大概念。其中，《普通高中信息技术课程标准》（2017年版）（以下简称“高中课标”）提炼出四个学科大概念，分别为“数据”“算法”“信息系统”和“信息社会”，《义务教育信息科技课程标准》（2022年版）（以下简称“义教课标”）亦提炼出六个学科大概念（也称六大逻辑主线）。这些学科大概念是信息科技课程内容的基本框架。特别是高中阶段，课程内容标准、教材各单元及单元内各节内容均以四个学科大概念逐层分解而成的目标体系为内在线索。因此，前文所言信息科技课程各教学单元间无清晰的内在关联，是从计算思维培养的角度所得结论。从学科大概念的角度看，以课程标准及教材为依据的各教学单元则是线索清晰的整体结构。

然而，在当下基础教育语境中，还无法以围绕学科大概念形成的目标体系为中介或桥梁，形成计算思维目标体系。原因如下：无论是各方学者对计算思维的界定，还是课程标准对计算思维及其水平的描述，均从计算思维“过程”角度出发，如“能在真实情境中发现问题，提取问题基本特征，对问题进行抽象、分解、建模……[6]”等。从描述角度和方式看，计算思维与“数据”“算法”等更倾向于“内容”（知识）的学科大概念在发展过程及水平方面并无直接关联。这与学界对思维“过程”与思维“内容”之关系的认识一脉相承。“知识（思维内容）是训练思维（思维过程）的材料，是思维调动、利用的资源[7]”。此论断在教育领域被普遍认同，其言下之意为，思维过程和思维内容间仅是调用与被调用的关系，二者在发展脉络及水平方面并无内在实质关联[8]。

于是，计算思维目标体系建构便遇到了一个难以逾越的瓶颈：一方面，从计算思维过程的角度，经多方努力，均无法形成多层关联的目标体系；另一方面，因计算思维过程与内容无内在实质关联，故无法以信息科技学科大概念目标体系为中介形成计算思维目标体系。困境就此产生。事實上，对于“思维过程与思维内容无内在实质关联”这一论断，教学实践中已经出现与其相悖的案例。例如，“敏捷性”是衡量思维品质的重要标准[7]，已有教学实践表明，增加知识（思维内容）节点间的关联可显著提升思维（思维过程）的敏捷性[9]。

源于对计算思维落地困境的担忧，亦因大量反例给予我们的追问动力，自2016年起，经过层层追溯，笔者及团队成员最终找到“思维过程与思维内容无内在实质关联”这一论断的直接来源——认知心理学关于学习核心机制的“信息加工”隐喻，并发现该隐喻的局限性[10]。在此基础上，从皮亚杰发生认识论之哲学精髓处获得启发，得到关于思维过程与思维内容间关系的新认识：思维过程与思维内容是本质上不可分的统一整体，这一整体可表现为两种状态：静态与动态。其中，静态即知识，是陈述性知识与程序性知识复杂交织的知识结构；动态即思维，是以既有知识结构为基础的知识结构再建构过程，其结果是新的知识结构的形成。此知识结构又是下一次思维运转的基础，如此螺旋上升，使得静态的知识结构与动态的思维结构在发展过程与水平方面保持同步和统一[8]。

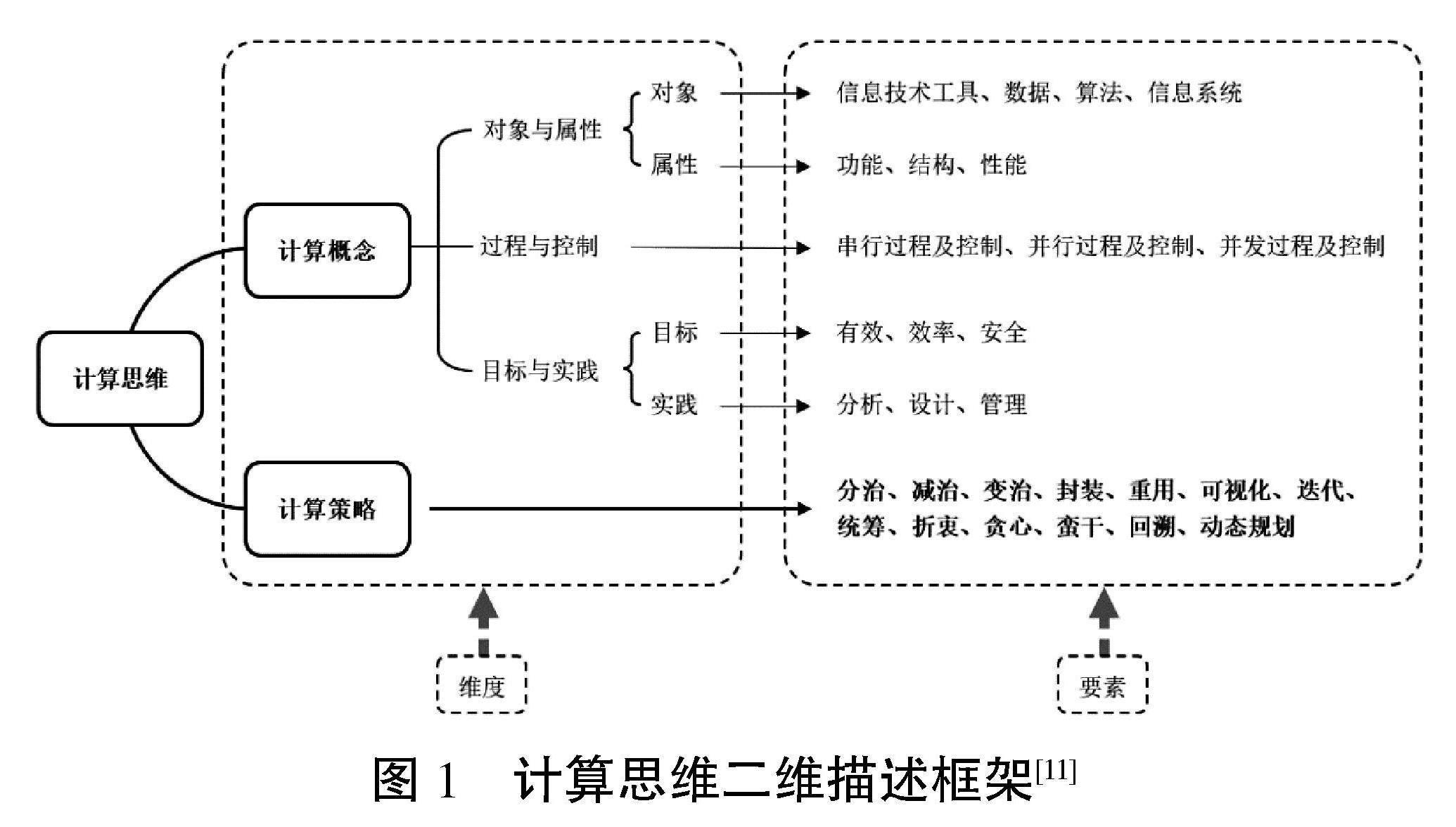
以“知识与思维内在统一”为基本立场，计算思维目标体系的建构困境便有了突破口：以与计算思维内在一致的学科大概念为中介，构建计算思维目标体系。以此为指导思想，以课程标准及教材为基础，并从上游学科——计算机科学中汲取智慧，我们最终建构完成与计算思维动态过程内在一致的静态大概念框架，包括计算概念与计算策略两个维度，如图1所示。其中，计算策略是核心。

图1   计算思维二维描述框架[11]

此计算思维二维描述框架（以下简称“描述框架”）中所含要素皆为学科层面的大概念，亦是计算思维目标体系的建构基础。基本建构思路为：将描述框架中的要素逐层分解，形成多层关联的概念“金字塔结构”体系；在此基础上，依据知识结构水平判断标准，结合课程标准中关于计算思维学段目标、学段特征等的规定，便形成可为各层面教学提供明确计算思维目标的多层进阶式目标体系。以此思路构建计算思维目标体系，亦可结束计算思维教学与课程内容（知识）教学两条线的尴尬局面，使信息科技课程呈现出主线清晰的一体化逻辑脉络和实践路径。

四、计算思维目标体系设计方案及例解

以计算思维目标体系设计基础及宏观思路为依据，本部分结合实例，给出具体详细的计算思维目标体系设计方案。

（一）计算思维二维描述框架各要素的分解和细化

在真实的教学场域中，“课”是教学的基本单位。就计算思维的有效培养而言，不仅单元，单元上层的模块、学段、课程，单元下层的课亦需要有明确的计算思维目标。因此，计算思维目标体系设计的第一步，便是对描述框架中的各要素进行分解，以保证每堂课、每单元等均有其聚焦的具体概念或大概念。以下分别阐释计算概念和计算策略维度要素的具体分解思路。

对于计算概念维度的要素，主要有两种分解思路：基于“整体—部分”关系的分解和基于“类属”关系的分解。例如，从类属关系的角度，“信息系统”可分解为“互联网信息系统”和“物联网信息系统”；从“整体—部分”关系的角度，“互联网信息系统”可进一步分解为“计算机系统”和“通信网络”……同理，计算概念维度的其他要素亦可依据此思路分解形成要素体系。

对于计算策略维度的要素，主要是基于类属关系的分解。以“分治”策略为例，从子问题之间关系的角度，“分治”可分解为“平行分治”和“递阶分治”① ；“递阶分治”又可分解为“逐步求精”和“递归”两种类型。从策略应用情境的角度，分解而成的以上要素还可进一步分解，具体如图2所示。依据不同的分类标准，计算策略维度的其他要素均可分解成层层关联的金字塔结构。

图2   计算策略维度要素分解实例

（二）知识结构水平判断标准的确定

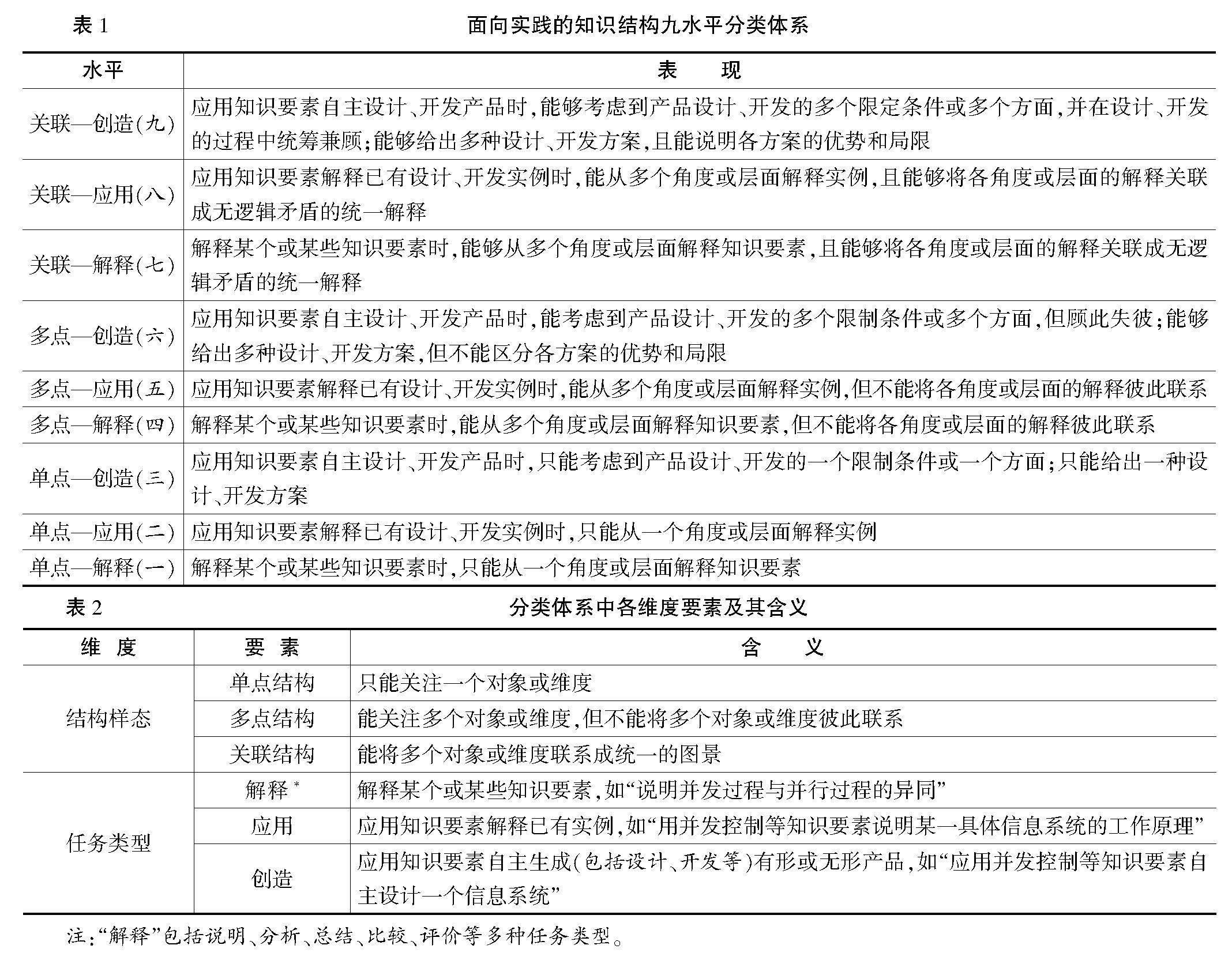
以发展计算思维为目的的知识教学，不再聚焦独立的知识要素，而是以促进众知识要素关联形成高水平的知识结构为旨归。换言之，虽然通过描述框架，将计算思维教学转换为特定范围内的知识教学，但这并非对传统知识教学的简单回归，而是否定之否定——从知识点转向知识结构。因此，需要一个以知识结构的复杂程度为水平划分依据的目标分类体系，其与分解而成的知识要素体系相结合，形成计算思维目标体系。SOLO目标分类体系基本满足此需求。该目标分类体系以思维结构（知识结构）的复杂程度为水平划分标准，共包含五个水平，由低到高分别为“前结构”“单点结构”“多点结构”“关联结构”及“拓展抽象结构”[12]。

然而，首先，“前结构”仅是一种理论样态，当知识结构为教学目标时，“前结构”并不适合作为其水平判断标准。其次，“拓展抽象结构”与“关联结构”并无知识结构复杂程度的差异，区别仅在于是否发生结构迁移[13]。再次，虽然从理论上，SOLO目标分类体系中“单点结构”“多点结构”“关聯结构”三个层级可以较为精准地标识知识结构水平，但在完成教学目标所要求的学习或评价任务时，学生需要激活、关联的知识要素往往多于教学目标显性要求的知识要素及结构，即有部分知识结构处于内隐状态。且对于知识结构显性要求相同的教学目标，涉及的任务类型不同，完成其所需的处于内隐状态的知识结构也存在差异，但一线实践者往往难以辨别这些内隐状态的差异。

鉴于以上，为了支持实践领域合理地确定知识结构水平，本文借鉴萨兰特（Salant）等人的思路[14]，将任务类型与SOLO目标分类体系中的“单点结构”“多点结构”“关联结构”三个层级相结合，形成了面向实践的知识结构九水平分类体系，见表1。相比“任务类型”，“结构样态”在水平划分时有较高优先级。分类体系中各维度要素及其含义见表2。该分类体系突破了萨兰特（Salant）等人所创分类体系仅面向编程领域的局限，可应用于所有教学场域。

（三）计算思维多层进阶式目标体系设计

以下笔者结合课程标准和教材，阐释如何以计算思维知识要素体系及知识结构九水平分类体系为依据构建计算思维目标体系。

义务教育及高中课标规划了前后相继的若干模块。故计算思维目标体系设计的一种易操作的思路为：将模块作为单元群的设计单位，以其为中心，向下分解形成单元进阶序列及课进阶序列；向上汇聚为学段进阶序列及课程整体，计算思维目标体系设计即是确定各层具体、明确的进阶式目标序列，如图3所示。以下从两个方面详解计算思维目标体系的设计方法：其一，各层目标中知识要素及知识结构水平的确定方法；其二，计算思维目标进阶线索。

图3   计算思维目标体系设计思路

1. 各层目标中知识要素及知识结构水平的确定方法

任何一个具体的计算思维目标均内含两个基本成分：知识要素以及知识结构水平。各层目标的抽象程度不同，主要表现为各层目标所含知识要素的抽象程度不同。其中，课程层目标中的知识要素即为描述框架中的要素，其余各层目标中的知识要素均在分解而成的要素体系中遴选。在描述目标时，不必将目标中显性要求的知识要素全部列出，只描述关键要素即可。对于知识结构水平的确定，因在目标统摄的范围内会包含多种水平的具体知识结构（这在宏观层面的目标中表现尤为明显），故以其中最高知识结构水平作为目标水平① 。需要强调的是，在设计各层计算思维目标时，无论是知识要素的选择抑或知识结构水平的确定，课程标准及教材均是重要依托，本文提供的计算思维要素体系及知识结构九水平分类体系则是对其进行以凸显计算思维的发展脉络为目的的二次创造的依据。

以计算思维课程层面的目标为例，依据本文给出的计算思维目标设计方法，对义教课标规定的计算思维课程目标进行二次创造，结果如下：“在真实问题情境下，通过数字工具支持的多种符形结合的表意及在线交流过程、数据分析与编码过程、算法设计过程及简单信息系统设计过程，初步理解过程与控制的基本原理，内化有效、效率、安全的目标意识以及可视化、分治、重用、迭代等计算策略，并将其迁移至其他学科及真实问题的求解中。”

从知识要素的角度，上述目标设计案例在保留义教课标所规定内容的基础上，从中提炼补充了若干计算概念（如有效、效率）和计算策略（如可视化、分治）。因目标处于课程层面，故所补充的皆为描述框架中的知识要素，且仅描述了关键要素。从知识结构水平角度，义教课标包含“互联网协议”这一教学内容，学生只有在教师的引导下（模拟）经历协议的初步设计过程，才能真正理解②协议本身，并内化其内含的“分治”“封装”等策略。设计互联网协议的过程需要各层统筹兼顾，故为“关联—创造”水平。即是说，义教课标要求学生本学科的知识结构（最高）水平为“关联—创造”水平。

除知识要素的遴选范围不同，其他各层计算思维目标设计思路与课程层目标基本一致，不再例解。

2. 计算思维目标进阶线索

目标进阶指目标的横向进阶，纵向上各目标间不存在进阶关系。图3中各层目标抽象程度不同，但进阶线索一致，即知识要素增加及知识结构水平提升。具体分为三种情况：与目标进阶脉络中的前一个目标相比，目标中的知识要素增加，知识结构水平不变；知识要素未增加，知识结构水平提升；知识要素增加，知识结构水平亦提升。

进一步，知识结构的发展过程是三种结构的螺旋上升过程（如“单点结构→多点结构→关联结构→多点结构→关联结构……”）。因此，知识结构水平提升可以有两种方式：第一种，同层提升，包含“单点结构→多点结构”“多点结构→关联结构”“单点结构→关联结构”三种情况；第二种，跨层提升，即螺旋上升后的提升，包含“关联结构→（跨层）多点结构”“关联结构→（跨层）关联结构”两种情况。再有，一般情况下，同一计算思维目标会与多个知识领域（目标进阶脉络）相关，进而表现出多个相对水平。

接下来以义务教育阶段《互联网应用与创新》模块的计算思维目标体系设计（图4）为例，详解计算思维目标的进阶线索。该设计实例中：将“单元二目标”置于互联网知识领域。因该知识领域要求学生从外在应用及内在原理两方面整体把握互联网，“单元一目标”聚焦互联网的外在应用，故其为“单点—创造”水平，包含的关键知识要素为“可视化”和“互联网工具”。“单元二目标”则要求学生在单元一的基础上，进一步（通过自主设计网络协议的方式）理解互联网的内在原理，初步形成对互联网的整体认识。相比“单元一目标”，“单元二目标”增加了“网络协议”“分治”等知识要素，目标水平进阶为“关联—创造”水平，属于前文所述第三种目标进阶方式。除了归属于“互联网”知识领域，“单元二目标”还可置于“分治”知识领域进行考察。结合课程标准和教材，可得到“分治”知识领域一种可能的目标进阶脉络：“将数字设备的使用过程分解为若干步骤（平行分治）→将数字作品的设计与开发过程分解为若干步骤（平行分治）→用算法描述解决简单问题的过程（平行分治）→將系统分解为若干子系统（平行分治）→初步（模拟）设计网络协议（递阶分治）……”将“单元二目标”置于此脉络中，其亦为“关联—创造”①水平。此外，“单元二目标”还可置于“封装”“统筹”“效率”等知识领域进行考察，从而在不同的进阶脉络中表现出相同或不同的目标水平。纵向角度，“单元二目标”与单元二内课层各目标间并不存在进阶关系；横向角度，单元二内课层各目标同样可置于不同目标进阶脉络中考察，进而表现出多种相对目标水平。篇幅所限，不再赘述。

图4   计算思维目标体系设计实例

综上所述，计算思维目标进阶脉络错综复杂，并非仅同层相邻目标间的简单关联。此是计算思维目标进阶的应然状态，同一计算思维目标亦因此表现出多种相对水平。鉴于此，在教学实践中，教师不必执着于确定特定计算思维目标处于何种水平，而应将关注点放在促进知识要素间建立尽可能丰富的关联上。这便要求教师在设计各层面目标时均有全局意识，如此才能真正引导、支持学生建构复杂关联的、高水平的与计算思维内在一致的知识结构。这正是本文给出的知识结构九水平分类体系之于教学实践的关键引导价值所在。

事实上，除了对计算思维目标设计的引导，知识结构九水平分类体系（任务类型维度）对于计算思维落地的另一关键要素——学习任务设计亦有重要的引导价值。受限于篇幅及本文主题，此处对学习任务设计仅作简要阐释（另文详解），以期为实践领域提供必要的方向性指导。依前文所述，在知识结构九水平分类体系的三种任务类型中，“创造”之所以水平最高，原因在于完成“创造”类任务需要学生在头脑中建构知识要素间更多、更复杂的关联，这正是教学过程的旨归。例如，图4中单元二便将“初步（模拟）设计网络协议”这一“创造”类任务作为学习任务。通过完成此任务，学生不仅能够深入理解互联网数据传输的内部原理，而且可以通过（模拟）经历这一“科学原理”的创造过程，内化蕴含其中的分治、统筹、封装策略以及效率这一目标意识。如此才能充分发挥“科学原理”教学对于计算思维发展的潜在价值[15]。反之，如果将单元二的学习任务确定为“应用”类任务，如“探究（解释）互联网中数据传输的内部原理”，那么依托此学习任务，学生习得的仅是科学原理本身，根本无法领悟蕴含其中的对于计算思维发展而言至关重要的计算概念和计算策略[11]。综上所述，在时间、资源等条件允许的情况下，应尽可能选择“创造”类任务作为信息科技课程的学习任务，形成以“创造”类学习任务为主，“应用”类学习任务为辅的信息科技课程学习任务体系。

五、结   语

本文始于信息科技课程中计算思维培养难成体系这一实践困境，并将困境原因归结为计算思维目标体系的构建困境。在此基础上，以“知识与思维内在统一”为基本立场，以计算思维二维描述框架及知识结构九水平分类体系为重要依据，给出信息科技课程中计算思维多层进阶式目标体系设计具体方案。该方案可结束信息科技课程内容教学与计算思维教学两条线的尴尬局面，使计算思维在与课程内容融合统一的教学路径中真正落地。

在后续研究中，我们将重点做以下两项工作：其一，在纵向上，以课程标准和教材为依托，系统梳理计算思维二维描述框架中各要素的进阶脉络，为教师从整体把握课程进而设计广泛关联的计算思维目标体系提供更充分的支持；其二，深入研究面向计算思维的学习任务及学习任务体系的设计方法，以支持计算思维目标体系有效达成。

计算思维对于学生未来发展的奠基作用毋庸置疑，但至今仍未有可落实于常规教学中的、成熟的计算思维培养体系。我们在为此努力，也期待更多研究及实践者的加入！

[参考文献]

[1] 冯友梅，王昕怡，刘晓蕊，张雪.计算思维不是什么：论计算思维的边界及其何以成为信息技术学科的立足之本[J].电化教育研究，2023（1）：84-90.

[2] 中国教育技术协会信息技术教育专业委员会.全国信息技术优质课资源[DB/OL].（2022-09-22）[2023-07-26].http：//112.15.150.219：8028/.

[3] 中华人民共和国教育部.普通高中信息技术课程标准（2017年版）[S].北京：人民教育出版社，2018.

[4] 张翠红.基于计算思维能力培养的单元教学设计[J].江苏教育研究，2019（33）：66-71.

[5] 陈兴冶，马颖莹.本土化计算思维评价指标体系的构建与探索——基于1410名高中生的样本分析与验证[J].远程教育杂志，2020（5）：70-80.

[6] 中华人民共和国教育部.义务教育信息科技课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[7] 林崇德.我的心理学观——聚焦思维结构的智力理论[M].北京：商务印书馆，2008.

[8] 馮友梅，颜士刚，李艺.从知识到素养：聚焦知识的整体人培养何以可能[J].电化教育研究，2021（2）：5-10.

[9] 胡卫平.胡卫平.关注方法和品质，有效培养学生思维能力[R/OL].（2022-01-27）[2023-07-26].https：//mp.weixin.qq.com/s/AskLJwy8tWcMKV34frjN2A.

[10] 冯友梅.支持素养教育的教育目标描述模型设计研究[D].南京：南京师范大学，2019.

[11] 冯友梅，王珊，王昕怡，周彤彤.支持我国信息技术课程评价体系构建的计算思维描述框架设计[J].电化教育研究，2022（6）：115-121.

[12] BIGGS J B，COLLIS K F. Evaluating the quality of learning—the SOLO taxonomy[M]. New York：Academic Press，1982：85.

[13] 王较过，赵欢苗.SOLO分类理论在物理教学设计中的应用[J].当代教师教育，2012（1）：57-62.

[14] MEERBAUM-SALANT O， ARMONI M， BEN-ARI MM. Learning computer science concepts with scratch[J]. Computer science education， 2013（3）：239-264.

[15] 冯友梅，王昕怡，温佳，马小兰，颜士刚.信息科技课程中“科学原理”的核心教学方法：归于算法，始于算理[J].现代教育技术，2023（7）：35-43.

Designing A Multi-level Progressive Target System for Computational Thinking in Information Technology Curriculum

FENG Youmei1，  WANG Xinyi1，   WEN Jia1，  WANG Zhuangwei2，  YAN Shigang1

（1.Faculty of Education， Tianjin Normal University， Tianjin 300387;

2.Hebei Provincial Teacher Qualification Accreditation Service Center， Shijiazhuang Hebei 050051）

[Abstract] Computational thinking is an important core competence in information technology discipline， but a structured teaching system for computational thinking has not yet been formed. Through analysis， it is found that the lack of an target system for computational thinking is the direct cause. In view of this， this paper takes "the internal unity of knowledge and thinking" as the basic standpoint， converts computational thinking into a knowledge structure， a two-dimensional descriptive framework of computational thinking， and designs the judgment standard of knowledge structure， a nine-level classification system of knowledge structure. On this basis， the design scheme of computational thinking target system combining the two is given and explained in detail with examples. Firstly， the elements in the two-dimensional descriptive framework of computational thinking are decomposed layer by layer to ensure that each teaching unit has its own focus on the elements of computational thinking. Then， based on the nine-level classification system of knowledge structure， a multi-level progressive target system of computational thinking is formed， which is vertically refined layer by layer and is horizontally upgraded in the level of computational thinking （knowledge） structure. This design scheme can end the embarrassing situation between content teaching and computational thinking in information technology curriculum， so that computational thinking can be truly realized in the teaching approach that is integrated and unified with the content of the course.

[Keywords]  Information Technology Curriculum； Computational Thinking； Target System； Multi-level Progressive System; Nine-level Classification System of Knowledge Structure