基于Volterra自适应滤波的SOC估计算法
2024-05-20广东电网有限责任公司湛江供电局龙雄峰陈小龙邓凯文
广东电网有限责任公司湛江供电局 龙雄峰 陈小龙 邓凯文
锂离子电池作为储能系统的主要动力能源,影响着储能系统的安全运行。电池SOC估算的精确性是和电池管理系统的性能息息相关,由于电池荷电状态SOC 是与很多因素相关联的,因此电池SOC 估算会比较困难,目前常用的SOC 估计方法主要分为两大类:第一类为传统方法,有内阻法[1]、放电实验法[2]、安时积分法[3]等,第二类为人工智能方法,主要有卡尔曼滤波法[4]、神经网络法[5]、最小二乘支持向量机等。
目前,基于神经网络的SOC 估算方法,基于支持向量机的SOC 估算方法可有效解决过度依赖模型,估算时间长的问题。此类算法不再依赖于锂离子电池模型结构以及电池参数,以电压、电流等参数作为输入,SOC 作为输出,进行大量的模型训练,此类算法完全基于数据,因此对数据质量要求较高。然而在实际工况中,锂离子电池的实时参数均由BMS 采集而得,但在BMS 实时监测中无法避免电流、电压信号的噪声及实时性差的问题。这对基于数据驱动的SOC 相关算法提出了较大的挑战。
混沌时间序列的建模和预测已成为近年来时间序列预测研究的一个热点。混沌现象是自然界广泛存在的一种不规则运动,是一种由确定的非线性动力系统生成的复杂行为。混沌信号本质的宽带、低噪声、对初始条件敏感、短期可预测等特点,使其在信号处理、通信、社会经济等领域中有着越来越重要的应用。
本文提出一种基于混沌时间序列的Volterra 自适应滤波器的SOC 预测,通过相空间重构技术,将电压、电流数据重构为多维度数据,揭示出电池SOC 与其他变量的相互关系,随后将重构后的多维度数据输入Volterra 自适应滤波器中,根据当前获得的SOC 预测值和当前的预测误差来不断修正模型参数。该预测方法可在较少的训练样本下,对电池SOC 混沌时间序列做出很好的预测,提高电池SOC的估算精度及训练网络的收敛速度。
1 锂电池SOC 混沌理论
1.1 相空间重构
相空间重构概念最早应用在统计学领域中,相空间重构就是将获取的一维时间序列拓展、延伸至三维或更高维数的空间,从而充分地把时间序列中所包含的动力学特征信息展示出来,根据拓扑等价来对原吸引子的动力学特征进行恢复。根据PACKARD 及Takens 定理,储能系统锂离子电池是一个多维动力学系统,其相关参数电压、电流、温度、内阻、容量也都是相应的时间序列,可以通过相空间重构,将一维时间序列重构成多维数据,即将混沌的状态还原到有规律可循的状态。设x1,x2,x3,…,xn为一维时间序列,则其相空间可以表示为:
式中,Yi为重构后的一维时间序列,为m×M矩阵,N为一维时间序列的长度,0为重构后的Yi长度,即重构相空间中的点数,τ为时间延迟。由此可得m维的重构相空间时间序列,且与原系统拓扑等价。
1.2 系统状态混沌特性
嵌入维数m 和时间延迟τ对混沌的判断十分重要。本文采用C-C 算法对嵌入维数m和时间延迟τ做计算,方法如下:
一是计算给定时间序列的标准差σ。
二是计算下列三个公式:
三是寻找式(4)的第一个极最小值点,即时间延迟τ,求式(5)的全局最小值点,即时间序列独立的第一个整体最大值时间窗口τw,求取嵌入维数的公式如下:
本文中采用改进的最大指数Lyapunov 法来计算该混沌时间序列的最大指数Lyapunov。
第一步是在重构相空间后,寻找给定轨道上每个点的最近临近点,即:
式中P为时间序列的平均周期,通过FFT 计算得到。
第二步是对相空间中的每个点Yj,计算出该临近点对的i个离散时间步后的距离dj(i)。
第三步对每个i求出所有j的lndj平均y(i),即:
其中q是非零dj(i)的数目,并用最小二乘法作出回归直线,该直线的斜率就是最大指数Lyapunovλi,判断一个时间序列是否混沌,较为简便的就是最大指数Lyapunovλi是否>0,如果是<0,则说明运动在处于收缩阶段,时间序列不存在混沌特性。
2 锂电池Volterra 自适应滤波
混沌Volterra 自适应滤波方法受到越来越多学者的重视,其可以准确地追踪混沌轨迹,广泛地应用于非线性领域中。该滤波器的原理图如图1所示。
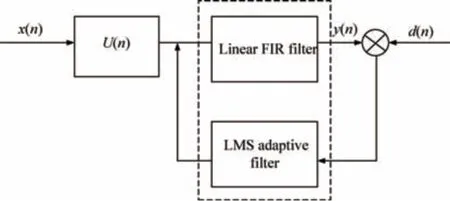
图1 Volterra 自适应滤波原理
设非线性离散动力系统输入为:X(n)=(x(n),x(n-1),…,0(n-N+1)),输出为则该非线性函数的Volterra 的展开式为:
式中,hp(m1,m2,…,mp)为P 阶Volterra 的核。由于无穷级数展开式在实际中难以实现,采用有限截断和有限求和的形式。非线性扩展后的信号为:
其中,U(n)为滤波器输入矢量,且m≥N1,N2实际应用中,滤波器的长度和从应为有限长,由嵌入定理知,一个混沌时间序列要完全描述原动力系统的动态行为,至少m>>2D2+1,D2为关联维数,取N1=N2=m≥N1,N2比如混沌序列Volterra 预测器模型选用二阶阶段求和模型时,模型如下:
状态扩展后系数的总个数为M=1+m(m(m+1))/2,定义线性自适应有限脉冲响应滤波器的输入矢量和系数向量为:
则该自适应滤波器的预测公式如下所示:
其中,预测相对误差的公式为:
该自适应滤波器采用的自适应算法为LMS 算法。
3 锂电池SOC 预测模型
3.1 试验系统
选用ZM7103电池性能测试仪作为电池数据测试平台,该性能测试仪适用于锂离子电池的性能测试,电压测量精确度为±0.1mV,电流测量精度为±0.1mA,试验采取的锂离子电池型号分别是LS CENS18650E,LR1865EH 的磷酸铁锂电池作为试验对象,两者额定容量都为1500mAh,可以在试验完成时及时保存电池实验数据,并存放到EXCEL文件中,便于后续的实验研究。
锂离子电池SOC 值无法通过测试获得,可通过其他参数,如电压、电流等推算获得,因此,该Volterra 自适应滤波器的输入为电池的电流、电压参数预测样本集的集合,输出为SOC 的预测值。通过当前获得的数据和当前的预测误差来不断修正模型参数,实现锂离子电池SOC 估算的闭环控制。采取三只额定容量为1500mAh 的电池作为试验样本进行SOC 预测分析,分别记为电池样本#1,电池样本#2,电池样本#3。采样间隔时间分别为60s、60s、15s。试验均在恒温箱内进行,温度控制在25℃±0.5℃,电池样本#1,电池样本#2,电池样本#3均循环3次采集各自电池的SOC 预测样本值。
3.2 电池SOC 预测模型
3.2.1 混沌特性辨识
以计算采集到的电池样本#1的SOC 时间序列的嵌入维数m,时间延迟τ为例,电池样本#2、3计算方法同上。锂离子电池样本#1的嵌入维数m=7,时间延迟τ=11,C-C 方法计算结果如图2所示。

图2 ΔS 平均图
由图2可以得出,第一个极小值是11,因此该混沌时间序列的时间延迟τ=11。
由图3中发现,Scor 的全局最小值点对应的是70,因此τw=70,由式(6)可以计算出此时的嵌入维数m=7。

图3 Scor 图
3.2.2 Volterra 自适应滤波器设计
Volterra 的阶数p 对模型的预测精度有很大的影响,研究学者多采用专家经验法来确定Volterra滤波器的阶数。针对电池样本#1,设定Volterra自适应滤波器的输入为电池的电压、电流,输出为SOC。将全部736组进行数据划分,前536组数据用于训练,其余200组数据用于测试。先确定滤波器的长度,由于电池样本#1的m=7,所以N1=N2=7。再进行非线性扩展,得到U(n),将U(n)输入到线性FIR 滤波器,输出预测值y(n),并与真实值作差得到误差e,将得到的误差e反馈给自适应算法,利用最小二乘法LMS 自适应算法求出该滤波器的系数向量H(n),最后再将重构后的测试数据带入训练好的Volterra 模型,求出最终的预测值。
故在常用p=2中对电池的SOC 进行预测,比较最后的预测相对误差Perr 和平均相对误差MRE,来确定Volterra 的阶数p。分别选取p=2,p=3,p=4,得到相应的测试曲线图以及绝对误差图(如图4所示)。
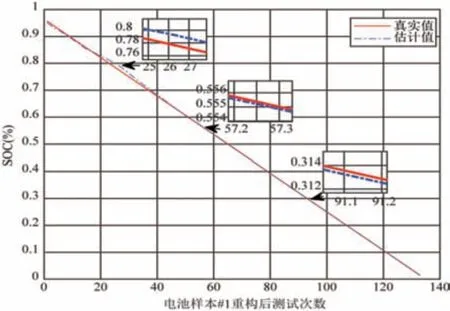
图4 当p=2时SOC 预测
上述三个阶数的误差对比见表1。
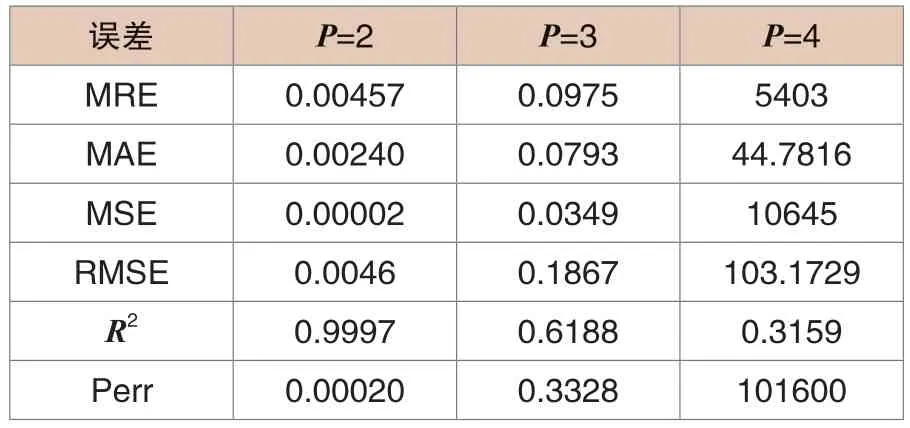
表1 不同阶数比较
p=3时局部误差太大,p=4的平均相对误差太大,而p=2时,平均相对误差较小。因此,Volterra 模型的阶数取p=2较为合适。
4 仿真和验证
混沌Volterra 二阶自适应模型。混沌Volterra二阶自适应模型在电池样本#1的SOC 预测中得到了良好的应用,其平均相对误差达到0.457%,决定系数R2也接近于1,说明拟合效果较好;均方根误差反映估计值的离散程度,越小说明离散程度越低,由此可见该模型可以很好地预测锂离子电池的SOC。
为了验证该模型的泛化性,预测电池样本#2并与电池样本#1作比较(#1,#2训练数据占总数据的70%),电池样本#2的预测图如图5所示。

图5 电池#2SOC 预测
电池样本#1,#2的误差对比见表2。

表2 电池样本#1and#2比较
由表2得:两种锂离子电池的预测相对误差Perr均小于0.001,说明该算法均可以有效地去预测不同型号的电池SOC。说明该预测方法具有很好的泛化性。
本文采用基于混沌时间序列的Volterra 自适应滤波器对电池SOC 进行了估算,首先利用小数据量法求得了最大Lyapunov 指数,求得每个Lyapunov 指数值都稍大于0,验证了锂离子动力电池SOC 时间序列具有混沌特性,其次通过相空间重构技术,恢复系统的多维非线性。将重构后的电池SOC 时间序列输入Volterra 自适应滤波器中,从而根据当前获得的数据和当前的预测误差来不断修正模型参数。本文研究SOC 估算算法误差不超0.6%。最后,验证了该自适应滤波器的泛化能力,通过对比训练数据和总数据的占比,分别比较了训练数据占总数据的40%和70%,发现当训练数据占总数据的70%时,电池SOC 预测效果较好,且随着Volterra 预测滤波器长度增大,Volterra 预测模型的精度也随之提高。
