基于BP神经网络的刀片切割竹枝性能研究

杨梦迪, 周兆兵, 孙 炜, 商庆清

(南京林业大学机械电子工程学院,江苏 南京 210037)

中国是世界上竹子资源最丰富的国家,中国境内拥有非常可观的竹林面积,根据“第九次全国森林资源清查”的最新数据显示,我国现有竹林面积为641.16万 hm2,占全国森林面积的2.94%[1-2],此外竹子还具有发达的根系,可以牢牢固定土壤,发挥保持水土、防风固沙等重要作用[3-4]。但是由于竹林生长周期较长,会引起竹林密度的过度增加,导致竹材的交错排列,对竹材的生长和质量产生一定的影响,进而导致竹子自行枯萎死亡[5]。为保证竹材的正常生长,需要对竹材进行打枝,竹枝打枝机中最重要的部分就是打枝刀的设计,而不同设计参数刀片切割竹枝性能是不一样的,如何验证刀片切割竹枝性能,更好地完成打枝过程,一直是竹材打枝机的研究重点。

国内外的学者对刀片切割性能方面作了大量研究,孙希同等[6]进行竹秆切割力研究,得到了竹秆切割过程中受到的刀片切削力约为94.38 N,刀片的最佳转速为1 155 r/min;王炳棚等[7]设计了双动刀切割试验台开展沙棘枝条切割试验,探究平均切割速度、刀具滑切角、刀刃高度和动刀组数对沙棘枝条切削力的影响;Li YX[8]对切割辣椒枝条的刀具进给角、刀具刃角、刀具进给速度进行了单因素和多因素有限元仿真试验,研究预测发现最大切割力为803.35 N,切割完成度为98.58%。

通过研究发现,国内外有关竹枝切割方面的研究较少,因此本文借鉴类似枝条切割方面的文献,以竹枝为研究对象,利用切割阻力作为衡量标准,探究刀片切割性能与关键参数(刀片的滑动角、楔角和滑动速度)之间的相互关系,为后续伐竹机械设计研究提供参考价值。

1 刀片切割性能试验

1.1 切割试验台

本切割试验台如图1所示,这一结构的组成包括直流电机、联轴器、卧式机架、数显推拉力计以及虎钳等。卧式机架由支架、丝杆、夹持组件和光滑杆构成。虎钳固定于机架的侧边,其作用是固定竹竿并保证刀片有效切割竹枝。虎钳的高度可调节,能够适应各种竹竿尺寸,从而保证切割效果的稳定性和准确性。在机架的另一侧搭载着一台直流电机,该电机用于控制刀片的滑切速度,并能进行正反转的精准调整,以便准确掌控刀片的前进和后退动作。直流电机的输出轴通过联轴器传动至滚珠丝杆,操纵着移动块的前后移动。同时,这一过程引导数显推拉力计前后运动,从而完成刀片对竹枝的切割和退刀动作。在这个过程中,刀片所承受的力瞬时呈现在数显推拉力计上,并记录下切割阻力的峰值数据。滚珠丝杆采用精密设计,以降低振动对数据准确性的影响。

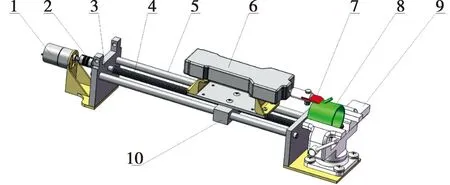
图1 切割试验台1.直流电机;2.联轴器;3.支架;4.丝杆;5.光滑杆;6.数显推拉力计;7.刀片;8.竹子;9.虎钳;10.移动块

1.2 试验内容

直流电机的速度变化范围为12～30 mm/s。为了便于计算,我们将刀片的滑切速度划分为三个级别:12 mm/s、20 mm/s和28 mm/s。同时,刀片的滑切角度也分为三个水平:45°、60°和75°;刀片的楔角也有三个水平对应:15°、18°和21°。这些具体的实验参数与各水平设定如表1所示。

表1 试验因素与水平

初次实验中,当刀片滑切速度为12 mm/s、刀片楔角为15°时,我们观察到刀片切割阻力与刀片滑切角度和竹枝直径的变化关系,具体数据记录见表2。

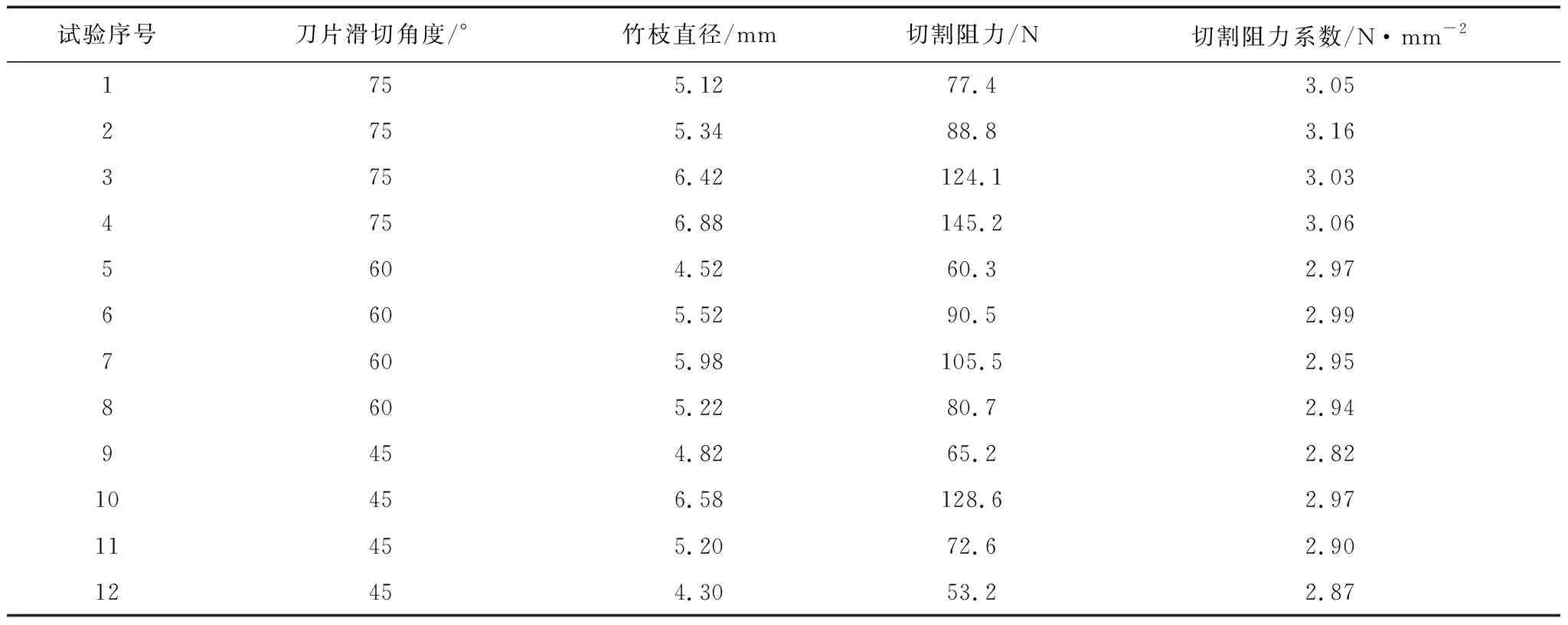
表2 不同滑切角试验结果

在第二组实验中,固定刀片的滑切速度为12 mm/s,滑切角度为45°,改变刀片的楔角至15°、18°和21°。部分试验数据见表3。

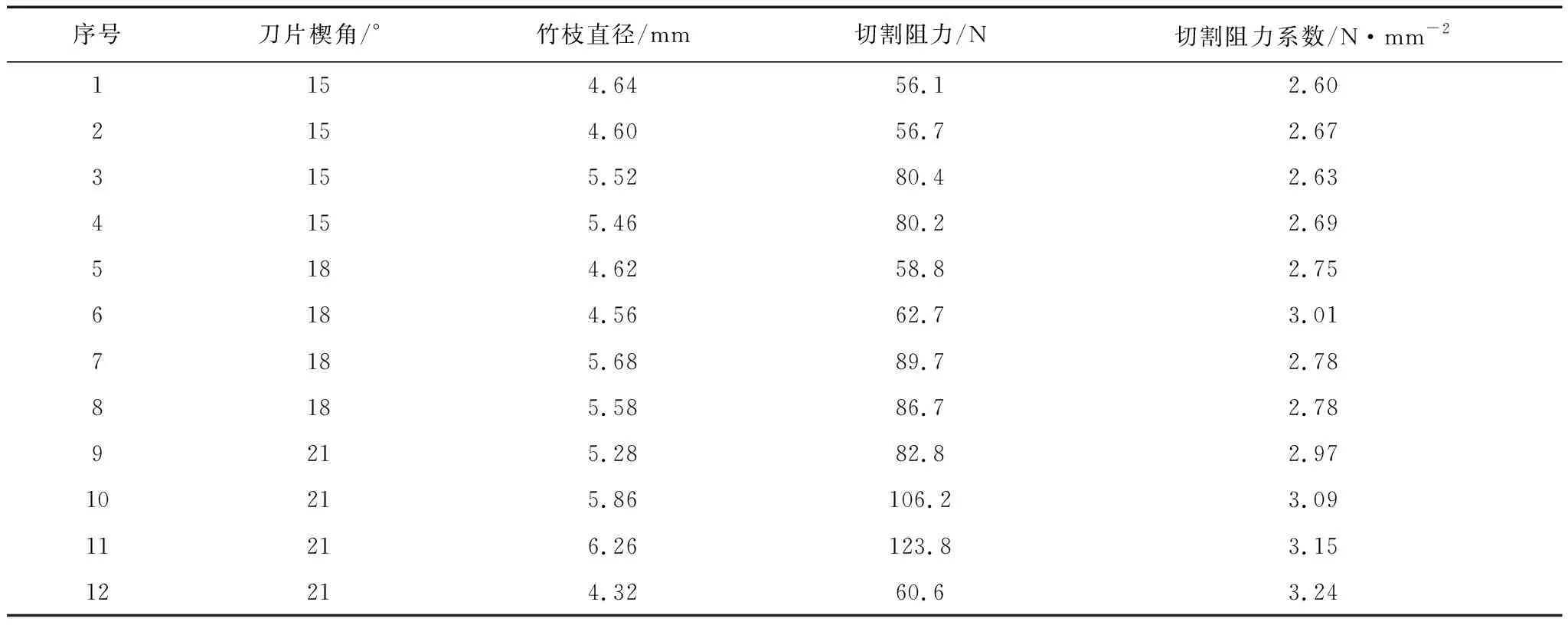
表3 不同楔角试验结果

第三组实验中,固定刀片的滑切角度为45°和楔角为15°。通过直流电机调速器,调整刀片的滑切速度至12 mm/s、20 mm/s和28 mm/s。部分试验数据见表4。

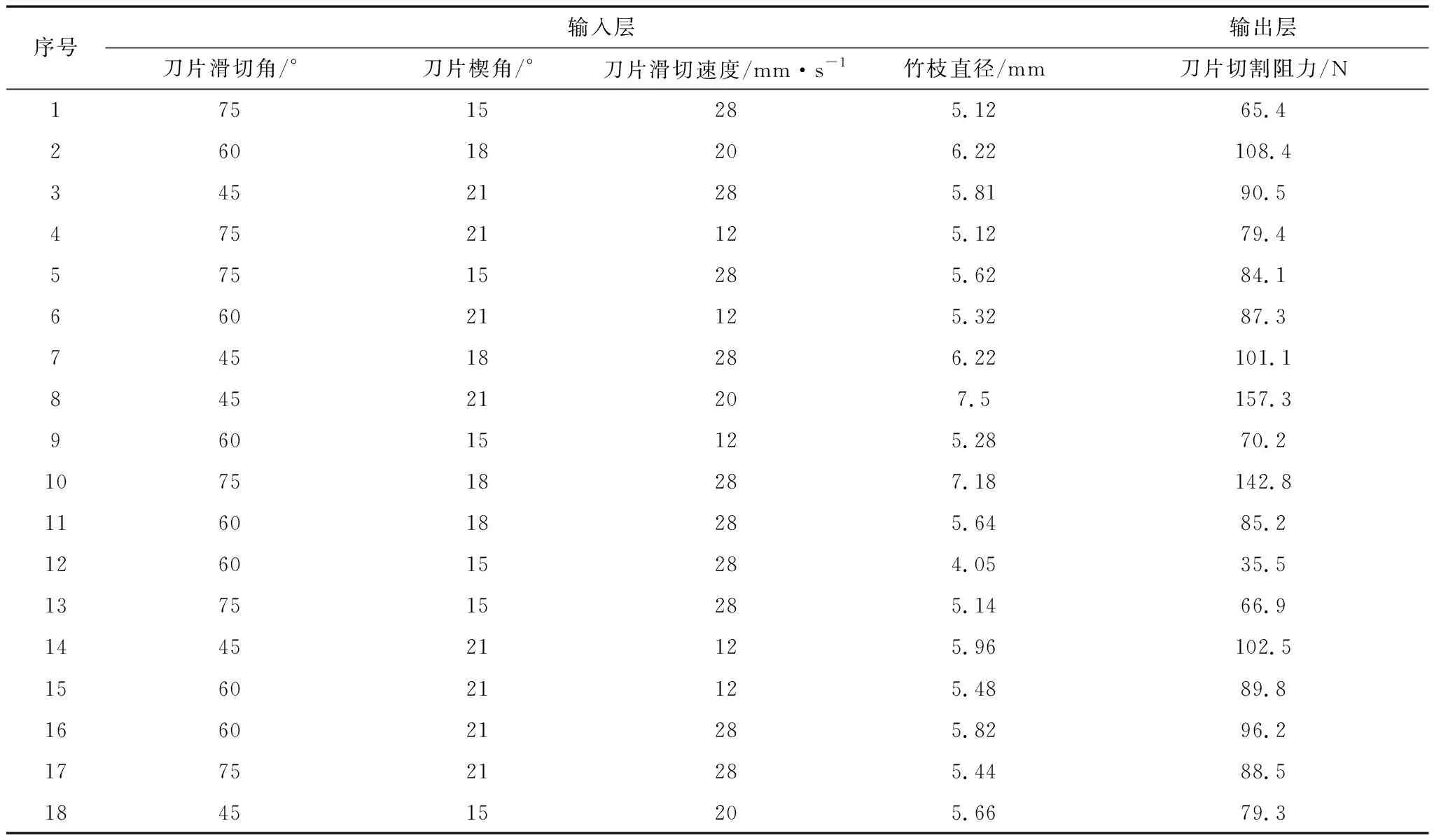
表5 BP神经网络数据集

2 基于BP神经网络切割性能模型

2.1 BP神经网络概述

BP(Back Propagation)神经网络,是一种多层前馈神经网络,其训练过程使用误差逆传播算法,通过不断调整不同神经元层之间的权重,以模拟和学习输入与输出之间复杂的非线性关系[9]。近年来,BP神经网络因其卓越的自适应学习能力、良好的容错性和高效的优化速度等特征而被广泛应用于数据拟合和结果预测领域,其运作方式模拟了生物大脑中神经元之间的信息传递过程,其中前馈层接收输入信号,将其传递给神经元进行处理,然后将处理后的信息传递给其他神经元[10]。

在一个三层BP网络结构内,可以借助经验公式来确定隐含层神经元节点的数量[11]。

(1)

式中:h为隐含层神经元个数;m为输入层神经元个数;n为输出层神经元个数;a为3～8之间的常数。

2.2 模型准备

2.2.1 数据来源

本研究中所运用的预测模型建立,借助了Matlab内置的BP神经网络工具箱。所采用的数据集均取自于刀片切割竹枝性能试验,采用不同的刀片滑切角度、楔角和滑切速度参数,对不同直径尺寸的竹枝进行切割,以收集的切割阻力的数据构成数据集,部分试验数据如表4中记录,刀片的滑切速度划分为三个级别:12 mm/s、20 mm/s和28 mm/s;刀片的滑切角度也分为三个水平:45°、60°和75°;刀片的楔角也有三个水平对应:15°、18°和21°。BP神经网络输入层分别为刀片滑切速度、刀片楔角、刀片滑切角度和竹枝直径,刀片切割阻力为其输出层。

2.2.2 数据处理

为防止因输入与输出数据之间显著的量纲差异而使训练受制于局部最小值问题,并对训练效果产生不利影响,通常采用归一化处理方法。这一方法有助于将数据重新映射到指定区间内的数值范围,从而提高神经网络的计算效率,降低误差。因此,在训练启动前,常规步骤包括对训练数据进行归一化处理[12]。归一化处理函数公式如式(2)所示。

(2)

式中,Ymax与Ymin分别为归一化后的区间端点值。本次预测模型Ymin与Ymax设定为-1和1,原始数据将由此映射到[-1,1]区间内;Yk为归一化后的数据;Xmax和Xmin分别为原始数据最大值与最小值。

2.2.3 模型建立

鉴于Matlab中的NTF APP(Neural Net Fitting 应用)可调参数不足以满足科研所需的参数设置,因此本研究采用脚本方式运行,以便更灵活地配置可调参数,并进行可视化分析。对数据集进行随机划分,分为训练集和测试集,比例分别为70%和30%。设定最大迭代次数为1 000,训练目标误差为0.001,学习率为0.001,同时将最小确认失败次数设置为200。在确定相关关键参数之后,通过将经过归一化处理的数据代入之前构建的网络模型,启动训练过程。具体的网络模型拓扑结构如图2所示。

图2 刀片切割阻力预测模型结构

2.3 模型结果与分析

2.3.1 网络训练结果

经过模型训练,将测试集数据输入已训练模型进行仿真测试。为了评估模型预测的准确性,采用决定系数R2作为评估标准,式(3)展示了其详细的表达式,由计算可知,决定系数R2的计算结果值范围在[0, 1]之间,越趋向于1表示模型的预测精度越高。

(3)

不同隐含层节点数训练结果决定系数见表6。

表6 不同隐含层节点数训练结果决定系数R2

制作条形统计图,以图形方式表现各个隐含层节点数训练模型的决定系数R2平均值,如图3所示:

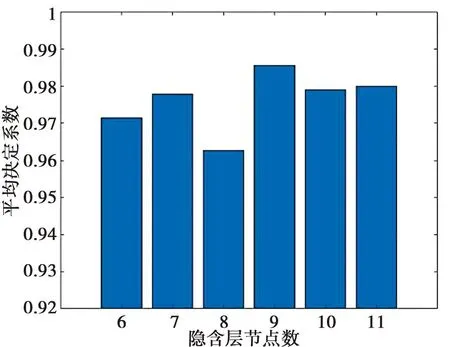
图3 不同隐含层节点数决定系数平均值

根据图3的数据显示,当隐含层节点数为9时,平均决定系数达到最高值,即0.985 6。这说明在隐含层神经元为9时,BP神经网络可以准确建立刀片切割阻力模型。根据图4的预测结果,预测值与真实值几乎完全吻合,只有少量出现误差,且误差很小。

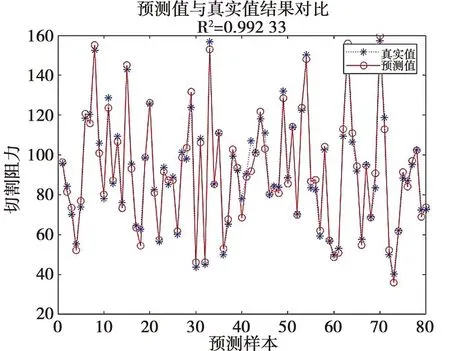
图4 预测值与真实值对比

分析图5中的神经网络工具箱训练评价结果,观察到所有标记点几乎呈线性分布。这表明本研究所构建的神经网络模型具备优异的预测性能,能够准确建立刀片切割性能模型。

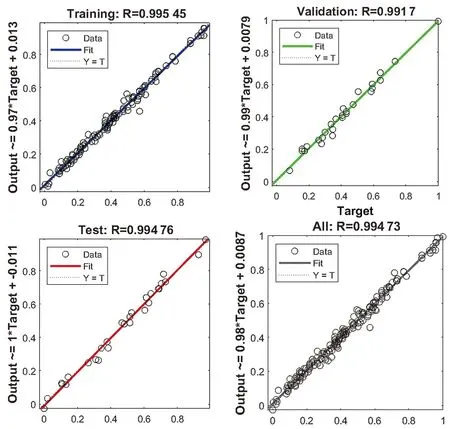
图5 神经网络工具箱训练结果评价

2.3.2 结果分析

由上述网络分析可以看出,当隐含层节点数设定为9时,可以成功建立刀片切割阻力模型,精准地预测刀片切割过程中的阻力变化,测误差可以保持在5%以内,对刀片切割竹枝性能研究具有一定参考价值。

3 结论

本文运用BP神经网络,建立了刀片切割性能模型,并就不同隐含层节点数与拟合性能之间的关联进行了深入分析。根据结果分析,当隐含层节点数设定为9时,可以成功建立刀片切割阻力模型,预测误差小,拟合效果好,对于对刀片切割竹枝性能研究具有一定参考价值。