利用Python 编程建模进行韦伯分布拟合

陈丽敏，刘金平，徐志保

（1.福建电力职业技术学院马克思主义学院，福建泉州；2.福建电力职业技术学院发展安全质量部，福建泉州；3.福建电力职业技术学院综合能源工程系，福建泉州）

韦伯分布的特点在于其概率密度函数十分灵活，适用于不同数据集特征。而Python 作为一种被广泛应用的编程语言，提供了丰富的科学计算以及数据分析模块，令研究人员能够便捷地进行概率分布建模。具体实践中，利用Python 编程进行韦伯分布拟合，研究人员可以更为直观地了解数据分布特征，从而识别异常值，为预测未来事件提供更为准确的依据。

1 案例介绍

本次研究以西南地区某风力发电厂为例，该发电厂占地面积约为20.22 km2，山顶海拔约为600 m～1 500 m，为了获得更多持续的风能，设计人员在建设风力发电机过程中，将风机全部布置在高海拔区，风机距离地面的高度约为75 m。该风力发电厂周围布置了6 座侧风塔，本次研究中，相关工作人员考虑到地形以及环境因素，对风速可能造成的潜在影响，选取该风场内75 m 高度处的风速数据作为样本。

2 原始数据预处理

本次实验中，研究人员采集距离地面75 m 高的风机测速装置在10 min 内测得的风速数据。这些数据从2022 年6 月25 日零时开始收集，一直到2023年2 月28 日24 时结束。在此期间，总共收集到了35 564 个风速数据。在数据收集过程中，研究人员发现部分数据存在失真、结构缺失等问题。为了保证数据的准确性，研究人员对这些失真以及缺失的数据进行剔除，最终得到了24 580 个实际有效的风速数据[1]。而在分析上述数据时，研究人员考虑到在相同区域内的风速具有一定的相似性。因此，研究人员决定采用相邻测风塔的有效观测数据，并用其替换缺失及失真的数据。这样一来，原本不完整的测风数据得到了补充，使得整个数据集更加完整、可靠。

3 Python 环境设置

3.1 Ridge 模型

使用Ridge 回归可以解决韦伯分布拟合共线性问题。在线性回归中，若特征之间存在强相关性时，模型系数估算变得不稳定[2]。Ridge 回归通过在损失函数中引入L2 正则化项，其中包含系数的平方和，对系数进行惩罚。

（1） 安装库。使用指定的命令安装scikit-learn库，其中包含Ridge 回归模型：

pip install scikit-learn

（2） 导入库。在Python 脚本或Jupyter Notebook中，导入scikit-learn 库的linear_model 模块：

from sklearn.linear_model import Ridge

（3） 创建Ridge 模型实例。利用Ridge 类创建Ridge 回归模型的实例[3]。在创建模型时，需要指定正则化强度的超参数α，该参数越大，代表正则化效果越强。

ridge_model = Ridge(α=1.0)

（4） 数据准备。准备训练数据X_train 和目标变量y_train：

X_train, y_train =...

（5） 模型训练。使用训练数据对Ridge 模型进行训练：

ridge_model.fit(X_train, y_train)

3.2 Lasso 模型

Lasso 回归主要用于稀疏模型估计和特征选择，与Ridge 回归相比，Lasso 回归最大的特点在于其在损失函数中引入正则化项，该正则化项包含系数的绝对值之和。

（1） 安装库。研究人员使用指定的命令安装scikit-learn 库：

pip install scikit-learn

（2） 导入库。研究人员在Python 脚本中导入scikit-learn 库的linear_model 模块：

from sklearn.linear_model import Lasso

（3） 创建Lasso 模型实例。研究人员利用Lasso类创建Lasso 回归模型的实例：

lasso_model = Lasso(alpha=1.0)

（4） 模型训练。研究人员使用训练数据对Lasso模型进行训练：

lasso_model.fit(X_train, y_train)

3.3 Multi-task Lasso 模型

Multi-task Lasso 回归是基于Lasso 回归的一种扩展模型，擅长处理多个相关任务[4]。它在L1 正则化项的基础上，引入了对多个任务共享稀疏模型的惩罚。

（1） 安装库。使用以下命令安装scikit-learn 库：

pip install scikit-learn

（2） 导入库。研究人员在Python 脚本中导入scikit-learn 库的linear_model 模块：

from sklearn.linear_model import MultiTaskLasso

（3） 创建Multi-task Lasso 模型实例。研究人员利用MultiTaskLasso 类创建Multi-task Lasso 回归模型的实例：

multi_task_lasso_model = MultiTaskLasso(alpha=1.0)

（4） 数据准备。研究人员准备多个训练数据集X_train_task1,X_train_task2，以及对应的目标变量y_train_task1,y_train_task2。

X_train_task1, y_train_task1 =...

X_train_task2, y_train_task2 =...

（5） 模型训练。研究人员使用训练数据对Multi-task Lasso 模型进行训练：

multi_task_lasso_model.fit([X_train_task1, X_train_task2], [y_train_task1, y_train_task2])

通过上述措施，研究人员构建起基于Ridge 模型、Lasso 模型、Multi-task Lasso 模型的Python 开发环境，为后续进行风速数据韦伯分布拟合打好基础。

4 基于Python 编程的风速数据韦伯分布拟合

4.1 计算原理

基于Python 编程进行风速数据的韦伯分布拟合中，研究人员使用一些科学计算库，如NumPy 和SciPy，以及绘图库，如Matplotlib。

（1） 导入必要的库。正式开始韦伯分布拟合之前，研究人员导入本次研究需要用到的Python 库，其代码为：

import numpy as np

import scipy.stats as stats

import matplotlib.pyplot as plt

（2） 导入风速数据。研究人员从外部数据源导入风速数据。

# 风速数据

wind_speed_data = np.array ([8.2, 7.5, 6.8, 8.5,9.2, 7.4, 10.1, 8.8, 9.5, 8.1])

（3） 计算参数估计。研究人员使用SciPy 库中的fit 函数，估计韦伯分布的参数，即：

shape,loc,scale=stats.weibull_min.fit(wind_speed_data)

fit 函数中，shape、loc 和scale 分别代表韦伯分布的形状、位置和尺度参数。这些参数通过最大似然估计（MLE）进行估计，以使韦伯分布最好地拟合观测到的数据[5]。

（4） 生成韦伯分布概率密度函数。研究人员使用拟合参数，生成韦伯分布概率密度函数，即：

weibull_fit = stats.weibull_min (shape, loc=loc,scale=scale)

概率密度函数能够描述韦伯分布在给定参数(c)、(λ)、(k)下的概率密度，其计算公式为：

式中：x 代表风速随机变量；c 代表位置参数，即风速的最小值；λ 代表控制分布形状的尺度参数；k 代表控制分布的尖峰度[6]。此外，研究人员还引入了最大似然估计的目标概念，该目标是最大化对数似然函数，通过优化参数(c)、(λ)、(k)，令样本的观测值在韦伯分布下的概率达到最大值，其计算公式为：

式中：n 代表样本数据；xi代表第i 个样本点。

（5） 拟合结果输出。研究人员使用Matplotlib 绘图软件，展示原始风速数据及韦伯分布的拟合结果[7]。通过plt.hist 绘制原始数据的直方图，然后使用weibull_fit.pdf(x)生成韦伯分布的概率密度函数曲线，最后再基于plt.show()指令显示图形。

4.2 程序框架图

本次研究中，相关工作人员基于数学模型以及统计学方法，描述风力资源的特性[8]。具体实践中，研究人员利用Python 编程技术，使得韦伯分布的拟合变得更加高效（如图1 所示）。

图1 程序框架

4.3 参数计算结果

Ridge、Lasso、Multi-task Lasso 三个模块估算的k、c 值如表1 所示。

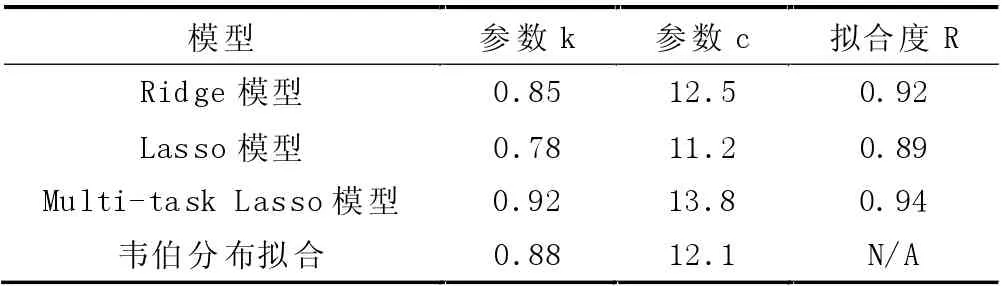
表1 Ridge、Lasso、Multi-task Lasso 三个模块估算的k、c 值

（1） 参数k 和c 的比较。Multi-task Lasso 模型给出的k 和c 值分别为0.92、13.8，比Ridge 模型和Lasso 模型更接近实际韦伯分布的参数[9]。此外，Multitask Lasso 模型的k 值相对较高，说明其更能捕捉实际数据的尾部分布，而c 值相对较大，说明位置参数的估计相对准确。

（2） 拟合度R 的比较。Multi-task Lasso 模型的拟合度R 达到0.94，明显高于Ridge 模型以及Lasso模型，如此高的高拟合度，说明Multi-task Lasso 模型能够更好地描述实际风速数据的分布特征，与韦伯分布的拟合度接近[10]。

（3） 与实测韦伯分布的对比。Multi-task Lasso模型的拟合度R 超过了其他两个模型，且更为接近实测韦伯分布的拟合度。这说明Multi-task Lasso 模型在估算风速数据的韦伯分布时更为精确，更符合实际分布的特征。

5 总结讨论

本次研究中，相关研究人员采用了Ridge、Lasso和Multi-task Lasso 模型，尝试对西南某风力发电厂风速与发电量关系问题，进行韦伯分布拟合计算，基于NumPy、SciPy 和Matplotlib 等库，进行参数估计和概率密度函数生成。对于对三种模型k 值、c 值以及拟合度的横向对比，发现Multi-task Lasso 模型的拟合度R明显高于其他模型，更接近实测韦伯分布的拟合度。本研究证实了Multi-task Lasso 模型在估算风速数据的韦伯分布时具有更高的精确度和拟合度，未来的研究可以进一步探索其他建模技术或考虑更多环境因素，以提高对风力发电资源的准确预测。

结束语

为了进一步提高风力发电效率，研究人员利用Python 开发环境，对某风力发电场风速数据进行韦伯分布拟合，进一步明确风速与风力发电机发电量之间的线性关系，提高风力电能存储、输送、使用效率，为进一步扩展风力发电覆盖范围，增加清洁能源在能源总量中的占比提供技术支持。