电磁波极化转换虚拟仿真实验教学探究
2024-05-17司黎明徐浩阳薛正辉
司黎明, 徐浩阳, 薛正辉, 丁 军
(1.北京理工大学集成电路与电子学院,北京 100081;2.华东师范大学通信与电子工程学院,上海 200241)
0 引 言
在电磁波的传播过程中,电场瞬时矢量尾端随时间的运动轨迹称作电磁波极化[1-2],在基础物理学中也被称之为偏振[3],是“电磁场与电磁波”课程中的一个极其重要概念。电磁波极化与频率、幅度、相位、角动量、能量等主要特征量一起,被认为是可有效传递信息的重要物理量,在通信、雷达、导航、安检、成像、电子对抗等领域具有重要的应用价值。电磁波极化作为一种信息传递资源,重要性日益提升,应用前景更加广泛,深入理解电磁波极化及其转换对电子信息类相关专业的学生具有十分重要的意义[4-6]。
虚拟仿真实验教学充分利用现代计算机与信息技术,可以拓展传统实验教学的时空维度,突破传统实验教学中的不足,提升学生创新和实践能力,受到国家教育主管部门和各高校重视[7-11]。在电磁场与电磁波课程教学过程中,学生通过虚拟仿真实验,不仅可以形象直观地“看到”电磁场与电磁波以增强实践能力,而且也可以通过虚拟仿真熟悉该领域的研究热点前沿提高思辨能力与创新能力[12-15]。
由于全波电磁仿真软件具有操作简单、界面智能化、直观化,广泛应用于电磁结构分析、传输线设计、天线设计、滤波器设计、集成电路等多个领域。这些全波电磁仿真软件均是通过使用数值方法求解频域或者时域麦克斯韦方程组而设计实现。在商业界和科研领域,目前主流的电磁仿真软件包括:基于时域有限积分的CST 微波工作室;基于有限元法的Ansys HFSS 和Feko;基于矩量法的Keysight ADS。
本文提出一种基于全波电磁仿真软件CST 开展电磁波极化转换仿真实验教学的方案,使得学生能够形象直观理解电磁波极化的概念、掌握电磁全波仿真的基本方法与流程、熟悉电磁超表面这一国际学术前沿,从而真正理解电磁波极化这一重难点概念,为后续相关课程学习、科学研究提供助力。
1 电磁波极化转换基本原理
从电磁波传输形式看,电磁波极化转换可以分为反射型和透射型。电磁波极化转换原理可以通过琼斯矩阵以及衍生的反射矩阵进行分析。
1.1 透射型电磁波极化转换超表面
对于透射型电磁波极化转换超表面,可以通过琼斯矩阵[16]来分析。
以沿着z轴入射的均匀平面波为例,其可用两个正交的极化分量表示:
透射型的电磁波极化转换过程,可以由以下方程描述:
式中:tx和ty分别表示透射波x和y方向电场分量,琼斯矩阵
琼斯矩阵的基本性质如下:
(1)琼斯矩阵相乘定理。如果入射波Ei依次进入多个电磁波极化转换装置,并且它们的琼斯矩阵分别为Ti(i=1,2,…,n),则最终透射波Et的状态可以通过琼斯矩阵的乘积表示为
(2)琼斯矩阵的反向传输定理。在直角坐标系下,如果入射电磁波经过的媒质是互易的,当电磁波从媒质的背面入射,则琼斯矩阵
(3)琼斯矩阵的变换定理。在直角坐标系下,如果对媒质进行一系列的变换,且M表示变换矩阵,则经过变换后的媒质的新琼斯矩阵
以线极化转交叉极化的透射型电磁波极化转换超表面为例,此处将对一个具有轴对称特性的各向异性超表面进行本征模式的分析,如图1 所示。黄色部分表示金属贴片,蓝色部分表示介质基板,超表面平行于xy平面,金属贴片两个对称轴分别平行于x和y轴。规定u和v轴平行于xy平面,与x轴正方向分别呈±45°夹角。
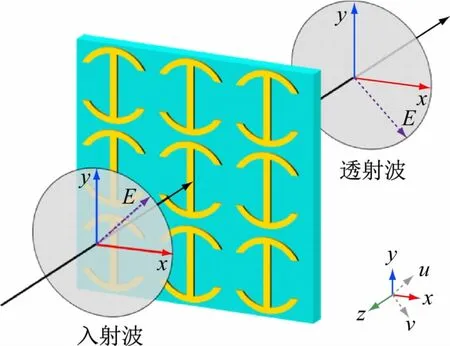
图1 透射型电磁波极化转换超表面示意图
透射型电磁波极化转换超表面关于xz面做镜像对称变换,超表面的形式不发生任何改变,因此琼斯矩阵也将不会发生变化,则根据式(6)可以得到:
根据式(7),可以得出此类超表面的琼斯矩阵形式为
当沿着-z轴方向传播的线极化入射波的极化方向为u方向且幅度为1 时,可以分解成极化方向为x和y的两个等幅度入射波的叠加:
此时可以实现将u极化入射波全部转化为v极化波。
1.2 反射型电磁波极化转换超表面
类似地,对于反射型电磁波极化转换超表面,也可以借用琼斯矩阵的形式,采用衍生的反射矩阵描述电磁波极化转换的过程。反射矩阵描述了入射电磁波与反射电磁波之间的关系为
式中,rx和ry分别表示反射波x和y方向电场分量。则反射矩阵
反射矩阵本质上是包含了极化特性的单端口散射矩阵,与琼斯矩阵相比不仅仅是能量传输形式上的区别。首先由于反射矩阵研究的是单端口的散射问题,所以不具备反向传输性质和相乘定理,其次根据互易性定理,反射矩阵的反对角线元素一定相等,即Rxy=Ryx。反射矩阵依然满足琼斯矩阵坐标系变换的一些操作。
图2 为反射型电磁波极化转换超表面的示意图,理想的反射型电磁波极化转换超表面可以将大部分的入射电磁波能量反射回去。该类结构往往由金属贴片、介质基板和金属地板三层结构构成。金属贴片和介质基板起到了控制反射相位的作用,而金属地的存在保证了反射效率。

图2 反射型电磁波极化转换超表面示意图
只要将透射型电磁波极化转换超表面分析中的琼斯矩阵T换成反射矩阵R,便可以得到反射型电磁波极化转换器,实现将沿-z轴方向入射的u极化平面波转化成与之正交的v极化平面波的条件:,且x和y极化波的反射相位差为π。
2 电磁波极化转换虚拟仿真实验
本文以一种基于金属ELC(Electric Inductive-Capactive)谐振器结构的线-交叉极化反射型电磁波极化转换超表面作为虚拟仿真的实验对象。反射型电磁波极化转换超表面的具体仿真实验流程主要分为以下4 步:①选取超表面单元介质和金属材料,并根据单元的工作频率、带宽等因素设计初步的单元形式。②利用CST的参数扫描功能,调整超表面的结构尺寸参数,将交叉极化反射幅度作为优化对象,获得最优的尺寸参数。③利用CST的数据后处理功能,对仿真获得的S参数进行数据处理,获得超表面单元极化转换率和能量转换率等性能数据。④在CST 中设置电流监视器,进行仿真,获得超表面单元在不同频点下表面电流的分布情况。
超表面单元的具体结构如图3 所示,由单层介质基板和两层金属层构成。最上层的金属ELC 谐振器结构和最下层的金属地板均选用材料金(电导率为45.6 MS/m),金属薄膜的厚度为t。中间层为介质基板,选用TOPAS 多聚物(相对介电常数为2.34,损耗角正切为7 ×10-5),厚度为h。TOPAS 多聚物在太赫兹频段上能够保持稳定的介电常数,并且拥有较低的吸收损耗,是理想的太赫兹介质基板材料。ELC 谐振器结构由分裂的圆环和短截线构成,沿x、y轴方向可以形成不同的谐振模式。
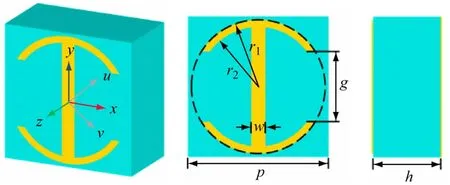
图3 基于ELC谐振器的电磁波极化转换超表面结构示意图
本案例使用CST对该结构进行仿真,定义入射波沿着-z轴方向前进。x、y轴方向均设置为unit cell边界,以模拟无限大周期阵列。电磁波极化转换超表面单元中圆环外径r1=48 μm,圆环内径r2=43 μm,上下环缝隙间距g=60 μm,短截线宽度w=10 μm,周期长度p=100 μm,介质厚度h=48 μm,金属薄膜厚度t=0.8 μm。实现的功能是可以将入射的u或v极化的线极化波转换为与其对应的交叉线极化波(u和v轴在xy平面内,与x轴夹角为45°)。
由电磁波极化转换基本原理分析可以得知,如果想要将入射的u和v线极化电磁波转换为与之正交的v和u线极化波,需要控制本征极化波即x和y极化入射波的反射相位,使它们之间存在180°的差值。除此之外,x和y极化入射波的反射系数的幅度要近乎相等且尽量接近于1,这样既能保证满足电磁波极化转换的条件,又能保证足够高的能量转换效率。
首先通过仿真得到x和y极化入射波的反射系数。得益于材料金较高的电导率和介质基板极低的损耗角正切,超表面单元产生的焦耳损耗和介质损耗较小,由图4 可知,0.2 ~2.0 THz范围内x和y极化入射波反射系数的幅度值均大于0.84。该仿真结果同时也证明了平行与垂直于反映面的x、y极化是该结构的本征极化,x和y极化波之间不存在互相转换的能力。
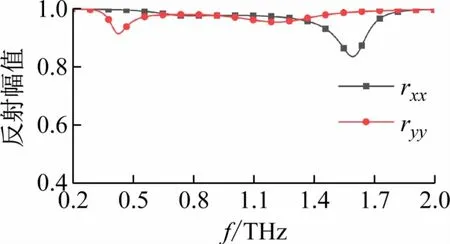
图4 本征极化波反射系数的幅度
根据图5 给出的x和y方向极化入射波的反射系数的相位,可以计算出本征极化波反射系数相位的差值。如图6 所示,在0.4 ~1.63 THz的频率范围内,x、y极化的反射系数相位差值围绕于180°附近。其中,0.43,0.68,1.23 和1.58 THz这4 个频点上的反射相位差值为180°。这些频点上,电磁波极化转换超表面由于严格满足实现电磁波极化转换的相位条件,将拥有接近于1 的极化转换效率。
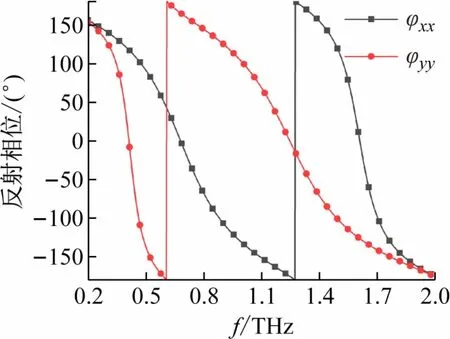
图5 本征极化波的反射相位
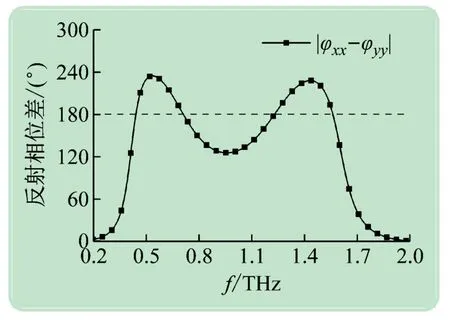
图6 本征极化波反射相位差
图7 表明当入射波为u和v极化线极化波时,在0.42 ~1.61 THz 内,交叉极化反射系数的幅度大于0.88。并且由于超表面单元的镜面对称特性,u和v极化入射波反射系数的幅度几乎一样。极化转换率(Polarization Conversion Rate,PCR)和能量转换率(Energy Conversion Rate,ECR)是衡量线-交叉极化转换器性能的重要指标,可以通过反射系数的幅度值计算得出。这里以入射波极化为u极化的情况为例,给出PCR和ECR的定义式:
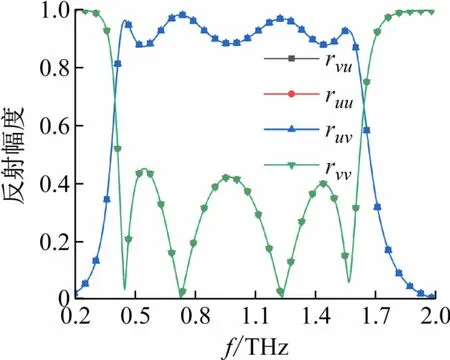
图7 u、v极化入射波反射系数的幅度
图8 和图9 为电磁波极化转换超表面的性能表现,在0.42 ~1.62 THz 内,PCR 大于80%,ECR 高于86.7%,相对带宽117.6%。其中,在0.45、0.73、1.24和1.58 THz这4 个频点,极化转换率超过99.9%。
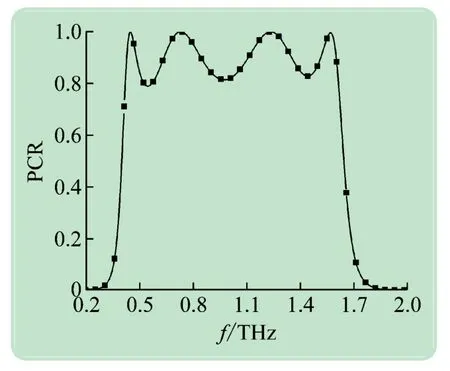
图8 电磁波极化转换率
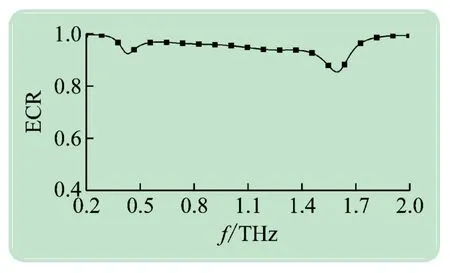
图9 电磁波能量转换率
当入射波的极化方向沿着u轴方向,在0.45、0.73、1.24 和1.58 THz这4 个频点上,电磁波极化转换超表面的极化转换率接近100%,下面将对电磁波极化转换超表面在这几个高极化转换率频点下的电流模式进行分析。根据图10(a),0.45 THz 频点上,ELC贴片沿着y轴方向产生了与金属地板上的电流方向相反的电流。电磁波极化转换超表面沿着x轴方向上具有较高的磁通,整体结构形成了磁谐振。
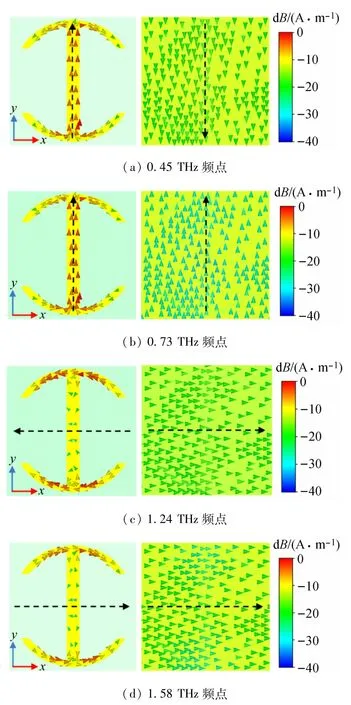
图10 ELC电磁波极化转换超表面电流分布
根据图10(b),0.73 THz频点上,ELC贴片沿着y轴方向产生了与金属地板上的电流方向相同的电流。电磁波极化转换超表面沿着y轴方向上具有较高的电通,整体结构形成了电谐振。
根据图10(c),1.24 THz频点上,ELC贴片沿着x轴方向产生了与金属地板上的电流方向相反的电流。电磁波极化转换超表面沿着y轴方向上具有较高的磁通,整体结构形成了电谐振。
根据图10(d),1.58 THz 频点上,ELC贴片沿着x轴方向产生了与金属地板上的电流方向相反的电流。电磁波极化转换超表面沿着y轴方向上具有较高的磁通,整体结构形成了磁谐振。
综上所述,电磁波极化转换超表面在这4 个频点上都产生了沿x轴和y轴方向的电矩和磁矩。与入射波极化方向成45°夹角的电矩和磁矩对应的电磁能量,又可以分解成入射波和与入射波电场方向相正交的反射波,最终就实现了线-交叉极化转换的效果。
3 结 语
本文搭建了基于CST 的“电磁场与电磁波”课程虚拟仿真实验,有力地支撑了课程实践教学。针对电磁波极化转换这一抽象概念,学生根据任务要求进行理论学习,建立全波仿真模型,并自行完成虚拟仿真实验内容,并对结果进行分析、对比、归纳和总结。学生对基本概念的理解更加深入透彻,同时通过数据分析与总结、参数优化和敏感度分析,培养了学生的科研创新能力。虚拟仿真教学可以有效地帮助学生理解电磁波极化及其转换,得到学生一致好评和高度认可。
