基于原型提取和聚类的光伏电站快速集群划分方法

2024-05-16陈文进杨晓丰祁炜雯王建军赵峰陈建国王健

浙江电力 2024年4期

陈文进，杨晓丰，祁炜雯，王建军，赵峰，陈建国，王健

（1.国网浙江省电力有限公司，杭州 310007；2.国网浙江省电力有限公司绍兴供电公司，浙江绍兴 312362；3.河海大学能源与电气学院，南京 211100）

0 引言

光伏发电作为一种可再生能源发电技术，具有推进能源转型、保护生态环境、减缓气候变化的作用，是我国实现碳达峰、碳中和目标的重要途径［1］。我国太阳能资源丰富，大多数地区的年平均日辐射量在4 kWh/m 以上，年日照时数大于2 000 h的地区占2/3以上［2］。光伏发电技术的成熟促进了光伏电站的大规模发展，在光伏发电渗透率不断提高的背景下，光伏电站的集群划分、出力预测、等值建模以及故障诊断等问题接踵而至［3-5］。因此，采用对应模型直接求解会面临求解问题规模过大、时间过长、效果不理想等问题。

应对大规模问题求解，现有研究均借助了聚类算法，对问题进行降维，将求解规模缩减到适当的大小后，再采用常规化方法进行针对性处理。文献［4，6-7］基于FCM（模糊C 均值算法）或其组合改进算法解决光伏电站功率预测、等效建模和故障诊断问题。张永新等［4］提出基于Canopy-FCM算法的分布式光伏电站等效建模方法，通过Canopy算法进行预处理，解决FCM对初始点的依赖性问题，提高光伏发电单元聚类等值建模的精确性。王开艳等［6］基于气象变量的数据特征提出了模糊C 均值聚类方法，将气象数据进行聚类，用于光伏功率短期区间概率预测，提高模型的预测性能。刘圣洋等［7］提出基于高斯核FCM 聚类的光伏阵列故障诊断方法，通过高斯FCM聚类算法对特征向量进行聚类，实现光伏阵列多重故障诊断功能，极大地提高了故障诊断的准确率。但是FCM系聚类算法解决大规模聚类问题的时间成本较大，对非凸数据集聚类问题并不适用。梁嘉文等［8］提出基于K-Mediods 聚类的分布式光伏台区线损异常感知算法，提高对分布式光伏线损异常数据的检测准确率，但K-Mediods 难以应对大规模聚类问题和非凸数据集聚类问题。董雪等［9］提出基于SOM（自组织映射网络）聚类的聚类方法，提高光伏出力的超短期预测精确率，但SOM易受网络结构影响，导致聚类结果出现较大差异且其自身收敛性不佳。王磊等［10］提出了基于Fast Unfolding聚类算法的分布式光伏电源集群划分方法，为配电网规划运行等提供技术支持，但Fast Unfolding 算法在解决大规模聚类问题时不易收敛，并且存在过拟合的问题。

现有的光伏聚类算法在一定程度上解决了光伏发电发展进程中存在的集群划分不合理、出力预测准确度不高、故障诊断误判率高以及等值建模不精准等问题，但仍有以下不足：当考虑多个时段的光伏数据时，数据集往往是非凸的，现有的聚类算法在应对非凸数据集上的效果并不理想；当面对较大数量的光伏电站聚类集群划分问题时，传统的聚类算法时间成本太大。

为弥补现有光伏聚类集群划分算法的不足，本文提出一种基于k-means++原型提取和改进谱聚类原型聚类［11］的光伏电站快速集群划分方法。该算法先采用随机抽样法从原数据集中抽取一定比例的样本数据，再基于k-means++算法进行光伏电站初次聚类，得到原型电站，实现光伏电站的原型提取，提高算法对大规模聚类问题的适应度。最后，基于谱聚类对非凸数据集聚类问题的适用性，采用改进谱聚类算法对原型光伏电站聚类，再根据就近原则完成所有光伏电站的集群划分，方便电站运行人员对光伏电站进行监测与管理。

1 原理介绍

1.1 光伏电站数据处理方法

1.1.1 光伏电站发电数据归一化处理

对任意一个分布式光伏电站的状态数据Xi=[Ai1，…，Aij，…，Aim]T，其中Aij表示第i个电站在第j个时段的运行状态数据。每个时段的运行状态数据都由多个气象数据与光伏出力数据组成，具体气象数据包括总辐照度、直射辐照度、散射辐照度、总云量、低云量、地面百叶箱气温、地面百叶箱湿度、地面10 m风速、地面10 m风向、空气质量、地面气压、每15 min 降水、总辐射、直射辐射、散射辐射和环境温度等16 类气象数据。各类气象数据的量纲和量级存在差异，需要进行归一化处理。按照同类物理属性进行归一化处理［12］：

式中：xmax为光伏电站某类发电数据的最大值；xmin为光伏电站某类发电数据的最小值。

1.1.2 光伏电站发电数据相关性分析

光伏发电数据中包含总辐照度、直射辐照度、散射辐照度、百叶箱气温、百叶箱相对湿度、地面10 m风速、地面10 m风向、总辐射、直射辐射和散射辐射等10 类气象监测数据。这些因素对光伏实际出力的影响权重大小各异，剔除影响权重低的因素能在一定程度上提高聚类效果。

Pearson 线性相关系数是较为常用的线性相关系数［13］，其计算表达式为：

式中：Rxy为自变量与因变量的相关系数，其范围从-1到+1，-1表示完全负相关，+1表示完全正相关，0 表示不相关；xi为自变量；yi为因变量；xˉ为自变量平均值；yˉ为因变量平均值；N为样本个数。

1.2 k-means++算法原理

k-means++算法与传统k-means算法最大的不同点在于对初始点的选择［14］。k-means++算法采用距离衡量法限定初始点的选择范围，确保在算法启动时，各个初始簇中心点具备较大的相异性。具体距离计算公式如式（3）所示：

式中：xj为第j个样本数据；ui为第i个簇中心；dj为第j个样本数据与前k个簇中心的距离和。具体算法流程参见表1。

表1 k-means++算法流程Table 1 Flowchart of k-means++ algorithm

1.3 改进谱聚类算法原理

SC（谱聚类算法）［15］源于谱图理论［16］，是基于图论的现代聚类算法，通过对数据之间的相似度构建拉普拉斯图，再使用切图算法把拉普拉斯图分割为若干个不相连接的子图，从而实现对样本的划分。传统的聚类算法如k-means 算法、FCM算法以及最大期望算法等在非凸数据上的表现较差，而SC算法却没有这个限制，对于不同分布的数据都有很好的划分效果［17］。

谱聚类算法主要为两个步骤：拉普拉斯图构建和拉普拉斯图切割。

1.3.1 拉普拉斯图的构建

拉普拉斯图构建的核心是邻接矩阵W的构建，对于k近邻内数据间的相似度计算方式如式（4）所示。

式中：wij为邻接矩阵W中第i行和第j列的元素，同时表示第i个数据和第j个数据的相似度；σ为带宽参数。

基于邻接矩阵W，按照式（5）、式（6）计算度矩阵D。

通过式（7）构建非标准拉普拉斯矩阵L。

通过式（8）对非标准拉普拉斯矩阵进行标准化处理，得到对称拉普拉斯矩阵LN。

上述是谱聚类算法中的拉普拉斯图构建方法。该方法在解决原型聚类问题时，其拉普拉斯图仅包含了原型数据间的相似度关系，忽略了原型与全数据集之间的关系［18］。为了解决此问题，改进拉普拉斯图构建方法［19-20］，按照式（9）和式（10）定义新的邻接矩阵W′。

根据新的邻接矩阵，通过式（5）—（8）得到改进的对称拉普拉斯矩阵。

1.3.2 拉普拉斯图的切割

给定一个无向图G，谱聚类的目标是将图G（V，E）分割为k个子图，其中V表示图中的点，而E为图中的边的集合，表示数据之间的相似度。切割出的k个子图分表表示为：{A1，A2，…，Ak}，这些子图之间的交集为空集，且所有子图的并集为全集。

对于两个不相交的子集A、B，定义它们之间的切为：

对式（12）进行扩展，定义所有子图间的切图权重：

切图的目标是最小化式（13），为了获得较理想的切图结果，采用归一化切图方法。归一化切图兼顾类内和类间的连接关系，定义为：

最终的切图问题转化为式（16）的优化问题：

式中：H为一个n行p列的指示矩阵。

式（16）是标准的迹优化形式，根据Rayleigh-Ritz定理［15］可知，该问题的最优解为L的前p个特征值对应的特征向量，将特征向量按列方向排序，组成解空间H∈Rn×p，对H的行向量执行一次kmeans聚类即可得到聚类结果。图1为改进原型谱聚类算法流程。

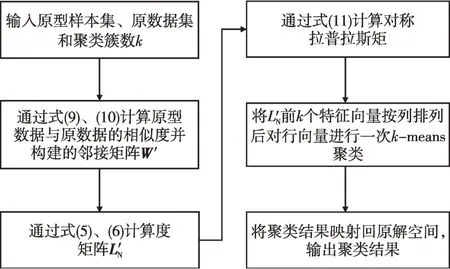
图1 改进原型谱聚类算法流程Fig.1 Improved spectral clustering algorithm for prototype

2 基于原型提取和聚类的光伏电站集群划分模型

2.1 基于k-means++算法的光伏电站原型提取

在光伏电站原型提取前，基于随机抽样法从原始数据集中抽取一定比例（η）的样本数据集。该步骤的预期目标是在保留原始数据集数据分布特征的前提下，有效缩减数据集大小。基于k-means++算法对抽样的样本数据集进行聚类，提取光伏电站原型。原型电站的提取比例（ρ）即k-means++算法的聚类中心占样本数据集的比例。超参数η、ρ的确定方法见2.3节。

对于任意一个分布式光伏电站数据Xi=［Ai1，Aij，…，Aim］T，其中Aij表示第i个光伏电站第j个时段的运行状态向量。

基于1.3 节给出的k-means++算法对光伏电站进行原型提取。显然，最终提取的原型依然是高维数据，为了可视化原型提取的结果，做如下处理：按照时段进行均值处理，消去时间维度；将处理后的数据向总辐照度、直射辐照度和光伏出力3个维度投影。从光伏电站中选取部分电站进行原型提取，得到如图2所示的光伏电站原型提取效果。

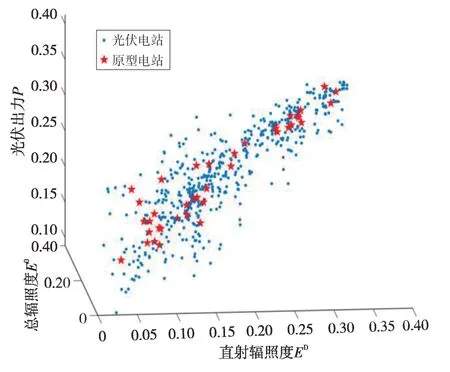
图2 光伏电站原型提取效果Fig.2 Extraction of PV plant prototype

由图2可知，将光伏发电数据向总辐照度、直射辐照度和光伏出力3个维度投影后，光伏电站发电数据显现较强的线性关系。通过k-means++算法进行原型电站提取，得到的原型电站用红星标注。

2.2 基于改进谱聚类算法的原型光伏电站集群划分

基于k-means++算法获得光伏电站原型，通过改进谱聚类算法对原型光伏电站进行聚类。改进谱聚类结果如图3所示。由于高维数据难以可视化，与图2相似，选择与光伏出力相关系数最大的前两个维度进行可视化。

图3 光伏电站原型聚类效果Fig.3 Prototype clustering of PV plants

图3中，红色五角星代表原型电站，黑色六角星代表中心电站。对比图2可知，原型电站仍然保留了原光伏电站的分布特性，但是图3中所展现的中心电站的分布在直观上并不具有代表性。这是因为在图像可视化的过程中忽略了其他维度的信息，导致可视化后的效果图代表性不强。

2.3 基于分层优化思想的聚类超参数搜索方法

在本文所提算法中存在3个超参数：随机抽样比例参数η、原型电站比例参数ρ和最终聚类中心数k。这3 个超参数的取值会影响最终的聚类效果。为优化聚类结果，找出合适的参数值，采用不同的超参数组合进行对照分析，比较不同参数值的聚类效果。在超参数搜索的方法上基于分层优化思想［21］，先划定3 个参数的取值范围，通过枚举法，遍历所有的取值组合，计算每种组合下的聚类指标，基于分层优化思想，根据聚类指标确定聚类超参数值。图4给出了聚类超参数的搜索思路。如图4所示，选定待聚类的光伏电站集群，采用η→ρ→k逐层优化的方式搜索每个超参数的取值。

图4 聚类超参数搜索思路示意图Fig.4 Schematic diagram of the search strategy for clustering hyperparameters

3 算法流程与聚类评价指标

3.1 算法流程

本文提出的基于原型提取和聚类算法的光伏电站快速集群划分方法主要环节有：光伏电站数据处理、基于随机抽样法的光伏电站抽样、基于k-means++的光伏电站原型提取和基于改进谱聚类算法的光伏电站原型集群划分。算法流程如图5所示。

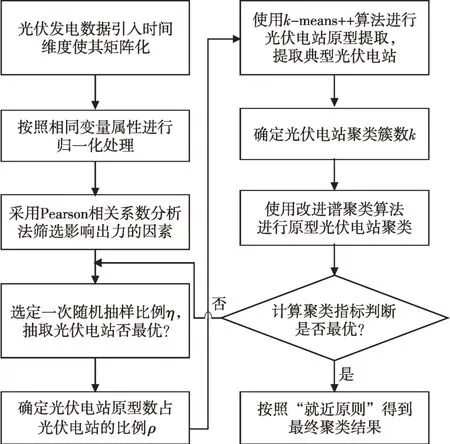
图5 算法流程Fig.5 Schematic diagram of the search strategy for clustering hyperparameters

1）光伏电站聚类数据处理。考虑到光伏数据包含多个物理量，量纲与数量级存在差异，对同类物理量采用归一化处理；再考虑到辐照度、风速、温度和气压等因素与光伏出力的相关性大小，采用Pearson相关系数法剔除弱相关因素。

2）基于随机抽样法对光伏电站进行初次抽样，在保留光伏电站分布特性的同时，缩减聚类问题求解规模。

3）基于k-means++算法对光伏电站进行原型提取，该环节与前环节一同起到聚类问题降维、提高聚类速度的作用。

4）基于改进谱聚类算法再对前一环节得到的原型光伏电站聚类，改进谱聚类算法对非凸数据集有着优良的聚类效果，再计算所有电站与中心电站的距离，根据“就近原则”得到光伏电站集群划分结果。

3.2 聚类评价指标

常用的聚类度量指标有DBI 指数（戴维森-堡丁指数）、DI指数（邓恩指数）、SSEI指数（平方误差和指数）和CHI 指数（卡林斯基-哈拉巴斯指数）［22］。

1）DBI指数

DBI 指数将类内紧密度和类间分散度综合考虑，如式（18）、（19）所示，其数值越小表示聚类的效果越好。

式中：avg(C)为类C内样本间的平均距离；|C|为类C中的样本总数。

DBI 指数的物理含义为类内距离与类间距离的比值，那么类内距离越小、类间距离越大则聚类效果越理想。

2）DI指数

DI 指标用于衡量样本紧凑度（类内最大距离）和簇群离散程度（类间最小距离），其定义如式（21）—（23）所示，DI值越大则聚类效果越理想。

式中：dmin(A，B)为类A与类B中最小样本距离；diam(C)为类C内最大样本距离。

DI 指数的物理含义为类间最小样本距离与类内最大样本距离的比值，那么类间最小样本距离越大、类内最大样本距离越小则聚类效果越理想。

3）SSEI指数

SSEI 指数是一个以样本与类中心点的距离平方和来度量样本的距离信息的指标，用聚类后数据样本中所有的子类中的数据到其隶属的类簇的聚类中心的欧几里得距离度量。

式中：ui为类Ci的类中心。

SSEI 指数的物理含义为各类样本与类中心距离和，其值越小则聚类效果越理想。

4）CHI指数

CHI 指数的本质是类间距离与类内距离的比值，也称为方差比准则。

式中：BG为类间差异矩阵的迹；WG为类内差异矩阵的迹；为第i类样本之间的平均距离；dˉ2为所有样本集之间的平均距离。

CHI 指数的物理含义为类间协方差与类内协方差的比值，所以类间协方差越大、类内协方差越小则聚类效果越理想。

5）综合指数

前文介绍了4种聚类指标，并未考虑聚类速度对聚类效果的影响。综合考虑多种指标的影响，按照式（26）定义综合指数CI。

式中：分子为负向指标，分母为正向指标，最终得到的CI指数也是负向指标，即CI值越小则聚类的综合效果越好。需要说明的是，式中出现的各个指标皆是通过式（1）归一化后的数值。

4 算例结果与分析

4.1 Pearson相关性分析结果

选用光伏电源数量为1 500的算例，将16种气象因素作为自变量，光伏电站有功出力作为因变量，根据式（2）计算得到各气象因素与光伏出力的相关系数，结果如表2所示。

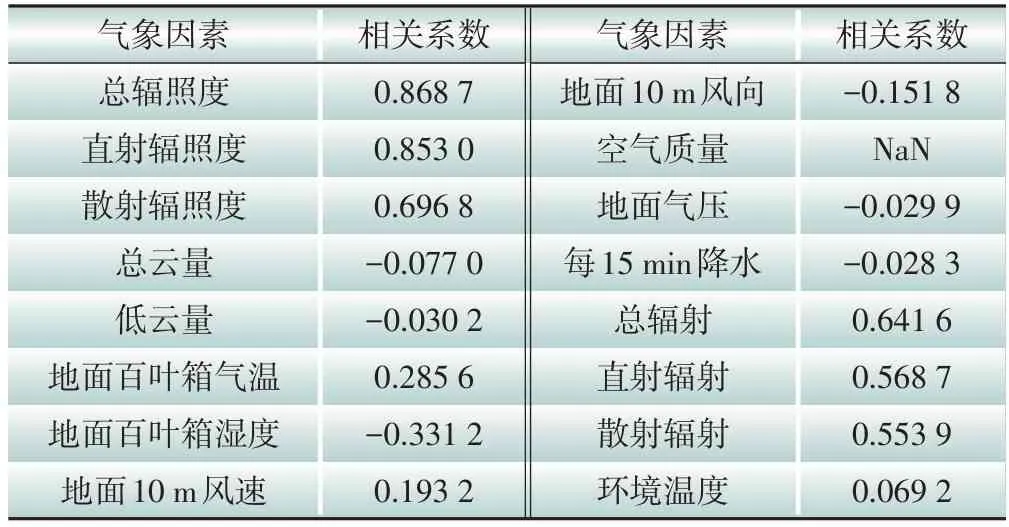
表2 气象因素与光伏出力相关系数Table 2 Correlation coefficients of meteorological factors and PV output power

当相关系数的绝对值小于0.1时，认为自变量与因变量之间不相关，反之，则存在相关性。根据表1结果分析可知，光伏出力与总辐照度、直射辐照度、散射辐照度、百叶箱气温、百叶箱相对湿度、地面10 m 风速、地面10 m 风向、总辐射、直射辐射和散射辐射等10类气象因素存在相关性。故在后续的研究中只保留上述10 种气象因素。需要说明的是，表2中空气质量的相关系数为NaN，因为该项数值都为同一数值，在本文中无法得出空气质量与光伏出力的相关性结果，故不予考虑。

4.2 聚类超参数搜索结果

孤例不证，为避免最优超参数选取的偶然性，本文设置3种算例场景，分别选择光伏电源数量为500（场景一）、1 000（场景二）和1 500（场景三）的3种算例场景进行聚类。如图6所示，将3种场景的聚类综合指标绘制成雷达图。

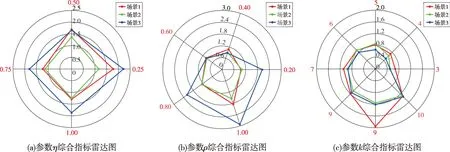
图6 聚类综合指标雷达图Fig.6 Radar charts of composite cluster indexes

判断每个超参数的取值优劣的依据是综合指数CI，当CI取最小值时对应的超参数即为最优超参数。图6 中，同心圆的半径对应CI 的值，CI 为负向指标，即半径越大则效果越差。因为本文关注重点并非是超参数的优化求解，所以通过简单枚举结合分层优化的方式确定了3 个场景中CI 值最小时对应的超参数取值。3个子图分别展示了3类超参数不同取值下的聚类综合指标结果。图6（a）给出了搜索最优参数η时的聚类综合指标雷达图，随着取值的递增，3 种场景下的CI 值并非呈现递减关系，当η取0.75时，本文所提方法在场景一和场景二都有较好的聚类表现，当η取0.5 时，所提算法在场景三的效果最佳，但综合考虑3个场景的聚类效果，选定η=0.75。图6（b）给出了搜索最优参数ρ时的聚类综合指标雷达图，当ρ取0.4 时，所提方法在场景一和场景三都有较好的聚类表现，当ρ取0.2 时，所提算法在场景二的效果最佳，综合考虑3个场景的聚类效果，选定ρ=0.4。图6（c）给出了搜索最优参数k时的聚类综合指标雷达图，当k取3 时，所提方法在3 种场景下都有较好的聚类表现，选定k=3。

4.3 算例对照分析

将所提方法与其他聚类算法作对照，进一步验证所提方法在光伏电站快速分群问题上的有效性。

除了本文所提聚类方法（算法4）外，另选择kmeans算法（算法1）、k-means谱聚类算法（算法2）和k-means++谱聚类算法（算法3），共计4 种算法作为对照算法，在3种场景下进行聚类计算并对聚类指标进行分析。整理4种算法在3种场景下的聚类结果，计算聚类指标值得到结果如表3—5所示。

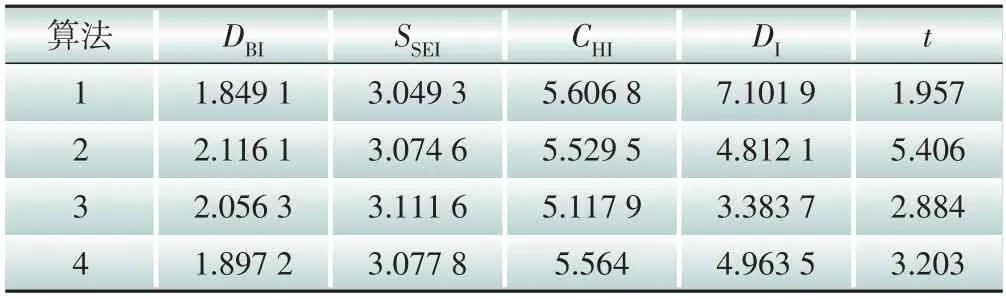
表3 场景一中各算法聚类指标值Table 3 Cluster indexes of each algorithm in scenario 1

表3、表4 和表5 分别为场景一、场景二和场景三下的4种聚类算法的聚类指标值。根据3.2 节的各指标定义可知，DBI、SSEI和t这3 个指标为负向指标，即指标值越小聚类效果越好；DI和CHI这两个指标是正向指标，即指标值越大聚类效果越好。为了更直观地比较场景与算法对聚类结果的影响，通过场景维度和算法维度，一纵一横两个角度进行对比分析。在分析场景对聚类结果的影响时，将对应场景下的4 个算法聚类结果取均值，得到各场景聚类指标对比图，如图7所示。在分析算法对聚类结果的影响时，将对应算法的3个场景聚类结果取加权均值，得到各算法聚类指标对比图，如图8所示。

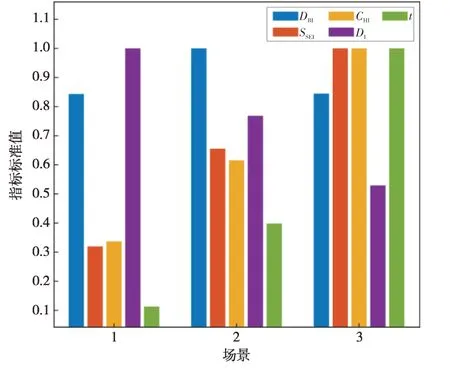
图7 各场景聚类指标对比Fig.7 Comparison of cluster indexes in each scenario

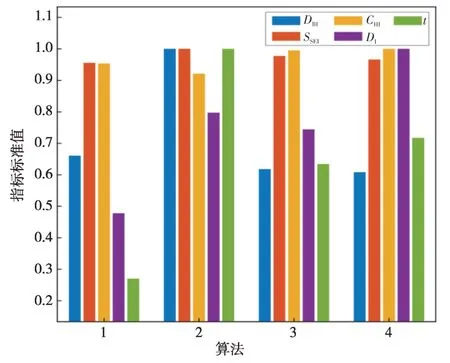
图8 各算法聚类指标对比Fig.8 Comparison of cluster indexes of each algorithm

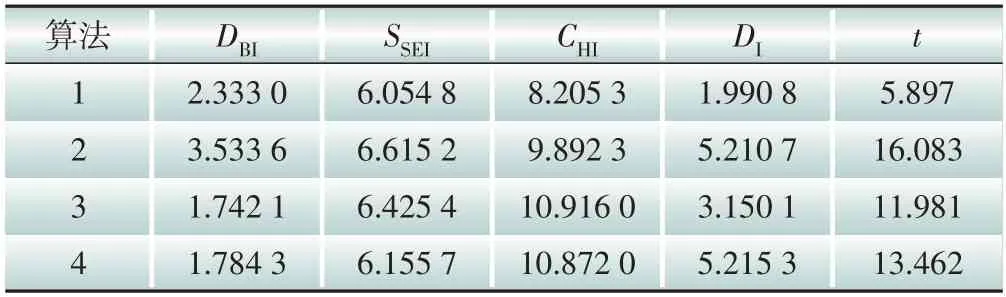
表4 场景二中各算法聚类指标值Table 4 Cluster indexes of each algorithm in scenario 2

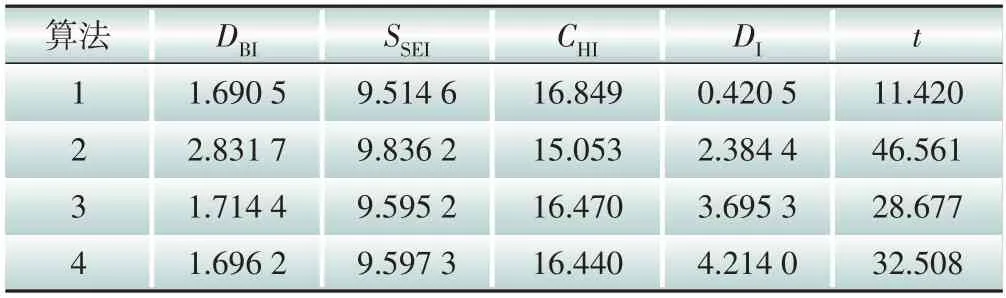
表5 场景三中各算法聚类指标值Table 5 Cluster indexes of each algorithm in scenario 3

需要说明的是，表格中的DBI、SSEI、CHI、DI和t等指标值未经标准化处理，但在图7和图8中，需要将所有指标展示在同一坐标系中，所以对指标值进行了标准化处理。

图7中给出了各场景聚类指标结果，根据对比可知，随着光伏数量的上升，负向指标数值呈现上升趋势，正向指标数值呈现下降趋势。说明随着光伏数量的上升，算法处理聚类任务的难度随之增大。图7 中的SSEI指标和CHI指标表现出了增长的一致性，但是SSEI指标为负向指标，CHI指标为正向指标，两者存在一定的矛盾。这表明不管是正向指标还是负向指标都有一定的局限性，所以为提高对照实验的可信度，算例对照环节需要参考对照多组指标。

将各算法在3 个场景下的结果加权平均处理，得到各算法聚类指标结果，如图8所示。在场景权重值方面按照场景一权重占比20%、场景二权重占比30%、场景三权重占比50%进行设定。

图8给出各算法聚类指标结果，算法1在时间上较其他算法有明显优势，传统k-means算法在3个场景的运行都十分迅速，但其余聚类指标较其他算法有着一定的劣势。这说明在应对本文所提问题上，传统k-means 算法聚类速度快但聚类效果不佳。算法2—4 对比算法1 在聚类时间上有着明显的提升，因为算法2—4 较算法1 增加了谱聚类的环节。同时，由于引入谱聚类环节，在一定程度上提升了聚类效果。

图7和图8从场景和算法维度对聚类指标进行对比，但多个指标大小各异，难以直观地对聚类效果进行综合评价。综合指标CI计算方式参见式（25）。在计算综合指标前，需对表3—5 中的指标数据进行标准化处理，标准化处理后的数据如表6—8所示。将计算得到的综合指标进行整理，具体结果如图9所示。

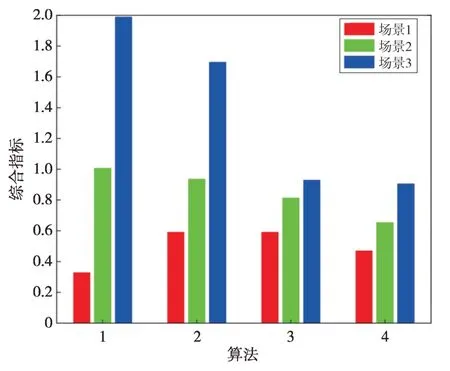
图9 各算法聚类综合指标对比Fig.9 Comparison of composite cluster indexes of each algorithm

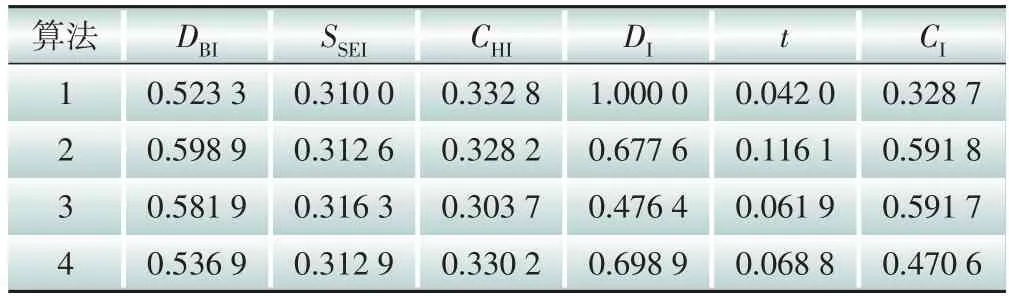
表6 场景一中各算法聚类指标Table 6 Cluster indexes of each algorithm in scenario 1

表7 场景二中各算法聚类指标Table 7 Cluster indexes of each algorithm in scenario 2

表8 场景三中各算法聚类指标Table 8 Cluster indexes of each algorithm in scenario 3

图9 中的算法1 是传统k-means 算法，不难发现：k-means 算法对计算规模有着较高的敏感性，其聚类综合指标随着聚类规模的增大呈现超线性增长，并且该算法较其余3种算法有着较为明显的劣势。算法2—4 都是k-means 系算法与谱聚类系算法的组合算法，该类组合算法基本上对聚类的规模不敏感，其聚类综合指标随着聚类规模的增大变化不明显。具体地，在这3种组合算法中，算法3 和算法4 都由k-means++算法组成。通过比较可知：这两种算法得到的聚类指标更加稳定，这是因为k-means++算法在挑选初始聚类中心点的过程中更加合理，避免陷入局部最优。通过对比算法3 和算法4 可知，算法4 即本文所提方法在处理较大规模的光伏电站聚类问题上有着更加优越的聚类性能。