考虑多类型电解槽差异化特征的分布式电热氢系统优化设计

张雪松，陈杨，倪筹帷，陈哲，李志浩，陈健

（1.国网浙江省电力有限公司电力科学研究院，杭州 310014；2.电网智能化调度与控制教育部重点实验室（山东大学），济南 250061）

0 引言

在“双碳”目标下，风机和光伏等可再生能源的大规模建设是降低碳排放的有效途径［1-3］。但由于风光出力具有强波动性和间歇性，给可再生能源的消纳和源荷实时平衡带来巨大挑战，导致了不同程度弃风弃光现象的出现。电解水制氢作为一种消纳新能源出力的有效途径，已在一些工业园区被广泛应用，因此出现了越来越多的分布式电热氢系统［4-6］。

分布式电热氢系统中，电解水制氢是最重要的一环，目前比较成熟的电解槽有3 种，分别是AEC（碱性电解槽）、PEMEC（质子交换膜电解槽）以及SOEC（固体氧化物电解槽）。其中AEC 技术最成熟、成本最低，但工作负载范围小、响应速度慢，电解效率为54%～66%。而PEMEC成本略高，负载范围更宽，响应速度更快，电解效率也有一定提升。但AEC 和PEMEC 的额定制氢效率均低于70%，相比之下，SOEC 电解效率可达到90%以上。但由于SOEC需要在高温环境下工作，其投资成本和响应速度仍落后于PEMEC。综上所述，AEC、PEMEC和SOEC分别在经济性、灵活性和高效性方面具有优势［7-13］，在具体使用场景中，应根据具体应用需求结合三者的特性差异，发挥它们的最大优势。

分布式电热氢系统中，风光发电的强波动性给电解槽的高效、稳定、经济运行带来了巨大挑战。在波动电源下，技术最成熟且经济性最优的AEC 的频繁启停和功率波动都会对其安全运行和制氢效率造成不利影响［14］。为此，文献［15-16］均采用电解槽和电储能配合消纳波动性电源的优化策略，利用蓄电池吸收风光波动功率，解决AEC无法快速响应的问题，从而提升电解槽运行效率。但是电储能设备属于短期储能，且存在自放电现象，对其增加投资将导致系统能量损失和运维成本的增加。相较于AEC，PEMEC 具有更好的动态响应速度［17-18］，能够迅速响应风光发电的强波动性，但PEMEC 过高的制造成本制约了其大规模应用。然而在制氢效率方面，AEC 和PEMEC均不及SOEC 有优势，但高昂的投资成本及高温运行条件导致其在经济性和灵活性方面有所欠缺。目前电热氢系统的优化设计研究中，对AEC与电储能配合AEC 和PEMEC 单独消纳风光出力的研究较多，较少有研究将3种电解槽的优势结合起来配合消纳具有强波动性的可再生能源的方案。

如何有机结合多类型电解槽差异化特征进行分布式电热氢系统的优化设计是一个重要问题。该问题的研究需要一个可以同时描述不同电解槽在经济性、灵活性和高效性等特性的统一通用模型以及优化配置框架和求解方法。关于优化配置框架和求解方法，目前文献［19-20］多采用双层耦合的求解框架，上层容量配置采用人工智能算法，下层优化模型采用求解器求解。关于电解槽的运行模型，文献［21-26］将电制氢过程处理为一个固定的电氢转换效率，并未考虑电解槽运行过程中的其他约束；文献［27-28］进一步考虑了电解槽启停约束，但没有考虑启停延时、爬坡速率等约束，对于灵活性描述不够充分；文献［9］建立了包括启停模型、产出模型及功率模型的电解槽统一运行模型，但忽略了电解槽的产热效应。

为了提升可再生能源利用率和分布式电热氢系统的经济性和环保性，本文从风光发电的强波动性和多类型电解槽的差异化特征出发，建立了考虑电解槽余热利用的多类型电解槽统一模型，该模型考虑了多类型电解槽的启停能力、产出特性、工作范围、爬坡能力、温度范围等特性参数。基于此提出了考虑多类型电解槽差异化特征的分布式电热氢系统优化设计方法，综合利用AEC、PEMEC和SOEC在经济性、灵活性和高效性方面的差异，使它们分别消纳不同波动特征的可再生能源，实现对多类型电解槽差别化利用，并根据运行结果优化设计系统中多类型电解槽、储氢罐、HFC（氢燃料电池）和各种储能设备的容量，使多类型电解槽的运行灵活性与风光出力波动性相匹配，充分利用AEC、PEMEC 和SOEC 在经济性、灵活性和高效性方面的优势，从而综合提升分布式电热氢系统的经济性和环保性。

1 分布式电热氢系统建模

1.1 分布式电热氢系统结构

分布式电热氢系统结构如图1所示，包括能量供给、能量转换、能量存储和能量消耗4 个部分。系统的能量供给为风机、光伏发电以及从上级电网购电，并通过能量转换设备进行电-热-氢转换，以满足不同能源的负荷。其中，电解槽包括AEC、PEMEC和SOEC，电解槽将系统中富余的可再生能源转化为氢气，在电力不足时，再通过氢燃料电池将氢气转化为电和热供给电负荷和热负荷。

1.2 电解槽数学模型

本文依据电解槽的启动延时、启停能力、产出特性、工作范围、启动功率、爬坡能力、温度范围等特性参数建立了适用于3种电解槽的统一模型，通过3种电解槽的参数不同进行区分。

1.2.1 电解槽启停模型

考虑启动延时的电解槽启停特性的数学模型如下：

1.2.2 电解槽产出模型

建立电解槽产出模型如式（6）—（7）所示。

1.2.3 电解槽功率模型

电解槽工作上、下限功率约束为：

电解槽爬坡功率约束为：

1.2.4 电解槽温度模型

建立的电解槽温度模型如式（11）—（13）所示。

1.3 储氢罐数学模型

建立储氢罐数学模型如式（14）所示。

1.4 热储能模型

建立的热储能模型如式（15）所示。

式中：Ht为热储能的储热量；Qch，t和Qdis，t分别为充、放热功率；和分别为充、放热效率；和分别为充、放热最大功率限值；Hmax和Hmin分别为热储能容量的上、下限；Ach，t和Adis，t分别为充、放热标志位。

1.5 蓄电池模型

建立蓄电池模型如式（16）所示。

式中：Et为蓄电池蓄电量；Pch，t和Pdis，t分别为充、放电功率；ηch和ηdis分别为充、放电效率；Pmaxch和分别为蓄电池充、放电最大功率限值；Emax和Emin分别为蓄电池电量的上、下限；Bch，t和Bdis，t分别为充、放电标志位。

1.6 氢燃料电池数学模型

建立氢燃料电池数学模型如式（17）—（19）所示。

2 分布式电热氢系统双层优化设计模型

2.1 上层容量设计模型

2.1.1 目标函数

上层目标函数为日净收益最大，其中，日净收益等于下层优化运行所得的日运行收益减去系统投资成本。通过设计电热氢系统各种设备（蓄电池、储热罐、储氢罐、燃料电池和多类型电解槽）的容量，使得系统日净收益最大。具体的目标函数为：

式中：下标i为不同的设备，包括碱性电解槽、质子交换膜电解槽、电储能、热储能、氢储能、氢燃料电池和电锅炉；Fup为上层优化设计的目标函数；Fdown为下层优化运行的目标函数；Cin为系统投资成本；N为综合能源系统中各设备总数；ηi为利率，取5%；ξi为各设备单位容量的投资成本；ti为各设备的使用年限；Si为综合能源系统中各设备的容量。

2.1.2 约束条件

综合考虑建设规模和建设条件等因素的限制，上层优化设计模型的约束条件包括多类型电解槽、氢燃料电池、储氢罐、储热罐、蓄电池和电锅炉等设备的容量约束，其表达式为：

式中：Si为各设备的容量；和分别为各设备容量的上、下限。

2.2 下层优化运行模型

2.2.1 目标函数

选取一天24 h 进行优化调度。以系统运行的经济性和环保性为目标，其中，在经济性目标中考虑设备启停费用、购电费用和售氢收益和售热收益，在环保性目标中考虑碳排放惩罚成本、弃风和弃光惩罚成本。优化运行模型的目标函数为：

1）经济性目标：

式中：f1为微电网与上级电网购电交易费用；为t时刻系统购电单价；Pbuy，t为系统在t时刻购买的电力；f2为电解槽启停成本；和分别为电解槽M的启动和关停成本；f3为售热售氢收益；ρheat为出售热的单价；Qsell，t为系统在t时刻售出的热能；ρH2为出售氢气的单价；为系统在t时刻售出的氢气；f4为储能使用成本；为储能单位使用成本。

2）环保性目标：

式中：α和β分别为弃光和弃风的惩罚系数；ΔPpv，t和ΔPwt，t分别为弃光和弃风功率；Kin为电-碳的转化系数；λcar为二氧化碳排放的环境惩罚因数。

2.2.2 约束条件

1）电功率平衡约束：

式中：ΔPpv，t和Pwt，t分别为光伏和风电预测出力；ΔPpv，t和ΔPwt，t分别为弃光和弃风功率；PEB，t为电锅炉消耗的电功率；Pload，t为电负荷。

2）热功率平衡约束：

式中：QEB，t为电锅炉产生的热能；Qch，t和Qsell，t分别为热储能充、放热量；Qload，t为热负荷。

3）氢气平衡约束：

4）购电功率约束：

式中：Pbuy，max为最大购电量。

5）电锅炉运行约束：

式中：ηEB为电锅炉电热转换效率；PEB，max和PEB，min分别为电锅炉出力的上、下限。

2.3 系统双层优化设计求解方法

上层优化设计模型中涉及多类型电解槽、多类型储能设备、燃料电池以及电锅炉等多种设备的容量配置决策。本文采用粒子群优化算法求解上层设备容量优化设计模型，采用Gurobi 求解器求解下层分布式电热氢系统优化运行模型，系统优化设计模型的求解流程如图2所示。具体求解步骤如下：

1）粒子群初始化

设置粒子群算法参数，包括种群规模、粒子维度、学习因子和惯性权重设定等，给定每个粒子的速度和位置的初始值。

2）计算粒子的适应度值

调用Gurobi 求解下层典型日优化运行模型，求出该容量配置结果下的日运行收益，减去等效日投资成本作为适应度值，并进行非劣排序。

3）更新粒子的位置和速度

首先给定粒子的位置和速度范围边界，并按照更新公式对粒子的位置和速度进行更新。每次更新后均进行边界检测，判断新粒子的速度和位置是否大于边界值，若大于则直接用边界值作为粒子的新位置和速度。

4）计算粒子新位置的适应度

再次调用下层优化运行结果并计算新的适应度值，按照适应度值的大小进行排序。

5）更新个体最优值和全局最优值

将新的种群粒子的适应度值与原适应度最优值进行比较，更新个体最优值和全局最优值。

6）终止条件判断

当最优个体的适应度达到给定的阈值，或者最优个体的适应度和群体适应度收敛时，或者达到最大迭代次数时，算法终止。

3 算例分析

3.1 参数设置

以图1所示分布式电热氢系统为研究对象进行算例分析，各设备容量配置参数如表1所示，多类型电解槽参数如表2所示［9］。

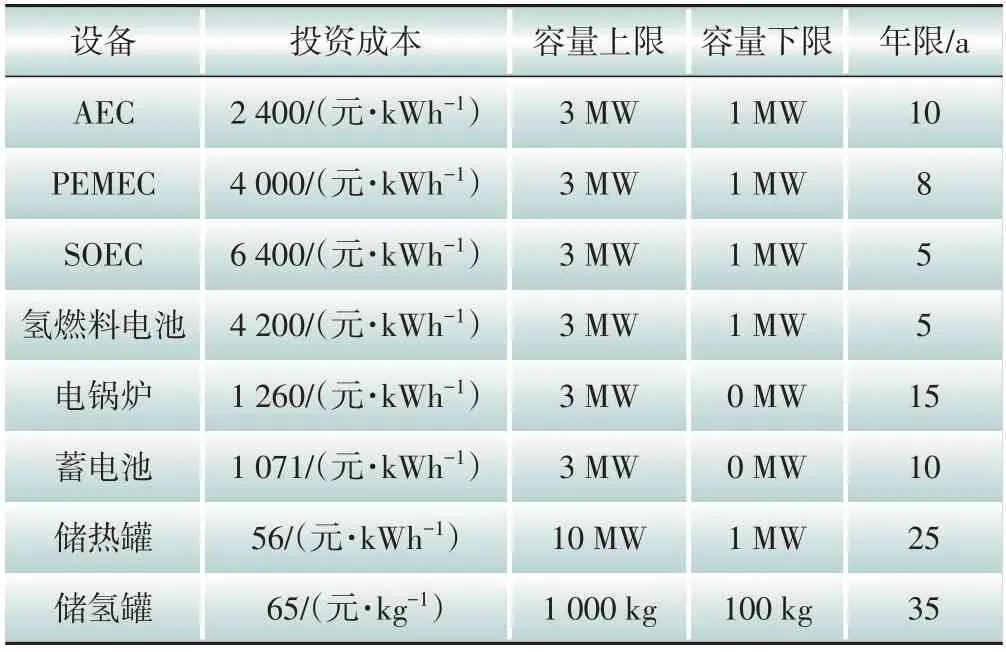
表1 设备容量配置参数Table 1 Equipment capacity configuration parameters

表2 多类型电解槽参数Table 2 Parameters of multi-type electrolyzers

分时电价如表3所示，储能设备、燃料电池和电锅炉相关参数参考文献［29］。本算例的优化运行层考虑夏季典型日和冬季典型日两种场景，两种场景的概率均设为0.5，图3 分别是夏季典型日和冬季典型日的风机和光伏以及电、热、氢负荷曲线。粒子群算法参数设置如下：迭代次数设置为100，群体粒子个数设置为300，学习因子为1.5，惯性权重为0.8。

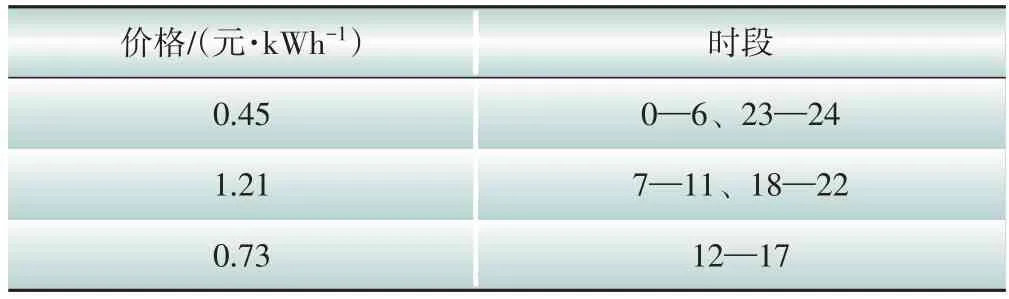
表3 分时电价Table 3 Time-of-use price

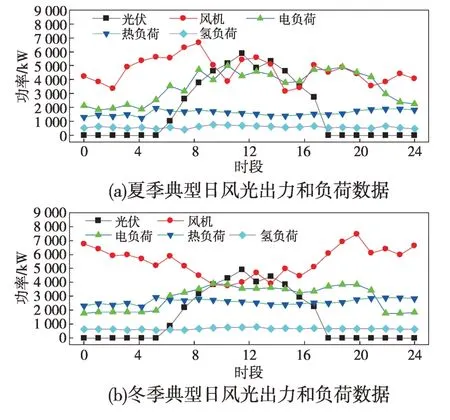
图3 典型日曲线Fig.3 Curves on typical days

3.2 算例结果分析

3.2.1 上层容量设计结果

上层求解时，将粒子群算法生成的容量配置结果代入夏季典型日和冬季典型日求其日净收益，将两者加权平均作为上层粒子群算法的适应度值，求解的收敛过程和上层容量设计结果如图4所示。

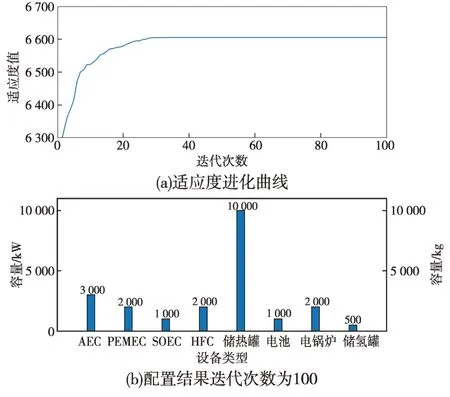
图4 粒子群算法收敛过程及容量设计结果Fig.4 The PSO convergence and capacity design results

为了对比多类型电解槽的不同配置比例方案下系统的经济性和环保性，固定电解槽以外的其他设备容量，并将3种电解槽容量之和固定为6 MW，改变AEC、PEMEC 和SOEC 的比例，使每种电解槽容量分别为1 MW、1.5 MW、2 MW、2.5 MW、3 MW，组合出19种配置方案如图5所示，结果对比如图5和图6所示，具体费用见表4。

表4 不同配置方案成本Table 4 Costs of different configuration schemes元

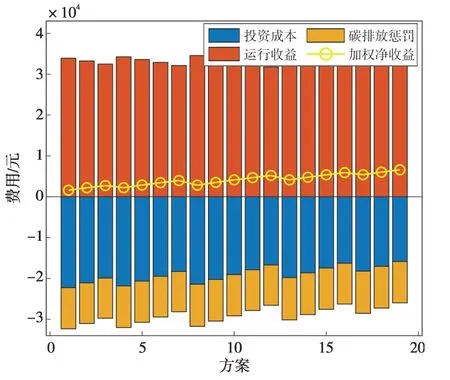
图5 不同容量设计方案结果对比Fig.5 Result comparison of design schemes with different capacities

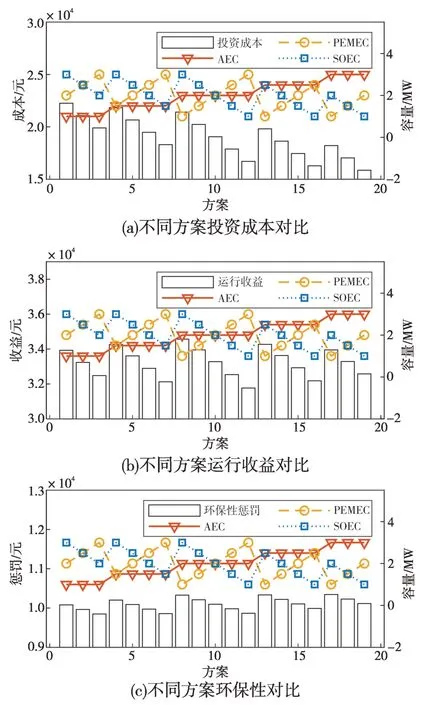
图6 不同容量设计方案特性对比Fig.6 Feature comparison of design schemes with different capacities

从图5和图6中可以看出，在经济性方面，由于AEC、PEMEC 和SOEC 投资成本递增，系统的投资成本随着AEC容量的增加而逐渐减少，在保持AEC 的容量不变时，随着SOEC 容量的减少和PEMEC 容量的增加而减少；运行收益随着SOEC 容量的减少而逐渐减少，因为AEC 和PEMEC 制氢效率低，SOEC 制氢效率高，SOEC容量的增加可以将同等电力转化为更多的高质量氢气出售，从而增加运行收益。图5中加权净收益为系统运行收益减去投资成本和环保性惩罚成本，加权净收益随着AEC的增加而逐渐增加，这是综合了AEC 的投资经济性和SOEC 的制氢高效性的结果。

在环保性方面，由于本算例的19 个容量设计方案中均未出现弃风和弃光现象，因此主要对比碳排放惩罚费用。PEMEC容量的增加会使碳排放成本减少，这是因为AEC 和SOEC 灵活性较差，而PEMEC灵活性较好，增加PEMEC配置容量也就增加了系统消纳具有强波动性的可再生能源的灵活性，减少了为适应可再生能源波动但受电解槽爬坡速率限制而导致的购电量，从而能够减少系统碳排放成本。

最终决策的配置方案为方案19，该配置方案中AEC、PEMEC和SOEC配置容量分别为3 MW、2 MW 和1 MW，AEC 灵活性较差且效率不高，但其投资成本低，用于降低系统投资成本；PEMEC灵活性强但投资成本较高且效率不高，用于灵活消纳波动性较大的可再生能源，降低系统环保性惩罚成本；SOEC 投资成本最高，但其效率高，用于提升系统运行收益。该方案使系统投资成本降低了28.74%，运行收益提升了2.55%，且环保性惩罚降低了2.22%，加权净收益最大，为本算例的最佳配置方案。

3.2.2 下层优化运行结果

以夏季典型日为例分析下层优化运行结果，本算例的容量设计结果可以实现风机和光伏的完全消纳。多类型电解槽运行结果和HFC运行结果如图7所示，多类型储能运行结果和系统功率平衡结果如图8、图9所示。

图7 夏季典型日多类型电解槽和HFC运行结果Fig.7 Operation results of multi-type electrolyzers and HFC on typical days in summer

图8 夏季典型日多类型储能运行结果Fig.8 Operation results of multi-type energy storage on typical days in summer

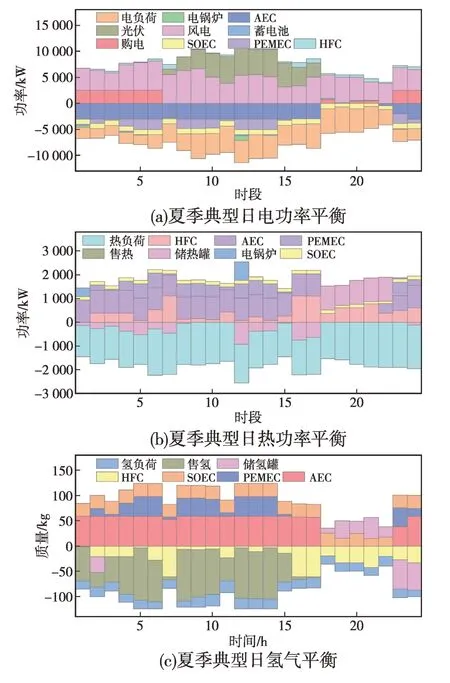
图9 夏季典型日系统功率平衡Fig.9 Power balance of the system on typical days in summer

从图7 中可以看出，由于PEMEC 爬坡速率快，灵活性强，其负责消纳可再生能源中波动性较强的部分；而AEC 和SOEC 由于产氢效率高，灵活性较差，负责消纳中稳定的部分。在18—22时段，由于PEMEC 已经处于关停状态，无法再通过调整其输入功率适应可再生能源波动，所以SOEC工作曲线也产生了小幅度波动。

从图8中可以发现，电储能、热储能和氢储能均在23—24 时段和0—17 时段处于储能状态。这是因为在0—6和23—24时段，负荷需求较小，且处于低谷电价，在7—17时段，光伏参与供能，系统能量较为充足，所以在这些时段储能系统将多余的能量储存起来；而在18—22时段负荷需求大，光伏无出力，且处于高峰电价，储能持续释放能量负荷提供足够的能量，储能起到了削峰填谷的作用。

从图9中可以发现，电价处于低谷时（0—6和23—24时段），系统购入了较多电能，不仅用于供给电负荷，也用于电解槽制氢和电锅炉产热；在7—17 时段，风光能量充足，不购电；而在18、20和21 这3 个时段，虽然处于高峰电价，系统也购入了少量电力，平衡系统的电能不足。从热平衡图可以发现，系统没有向外售热，只通过对电解槽和燃料电池的余热回收、热储能系统满足热负荷需求，以上都无法满足时用电热锅炉产热。从氢平衡图可以发现，在0—17时段系统向外大量售氢，这些时段中，0—6 时段时处于低谷电价，购入低价电力制氢出售，在7—17时段可再生能源充足，将多余电能转化为氢能出售，均能提升系统经济收益。

4 结语

分布式电热氢系统中电解水制氢技术可以将具有强波动性的可再生能源转化为高质量的氢气稳定利用。

本文针对分布式电热氢系统中风光出力的强波动性带来的挑战，围绕分布式电热氢系统建设中关键设备的容量优化设计问题，建立了考虑多类型电解槽的启停能力、产出特性、工作范围、启动功率、爬坡能力、温度范围和余热利用等特性参数的多类型电解槽统一模型；提出了考虑多类型电解槽差异化特征的分布式电热氢系统优化设计方法，该方法综合利用多类型电解槽在经济性、灵活性和高效性等方面的差异化特征；求出了本算例的最佳配置方案，使系统风光100%消纳，投资成本降低了28.74%，运行收益提升了2.55%，且环保性惩罚降低2.22%，净收益最大。