基于SWARA-CRITIC-MARCOS的负荷侧资源响应潜力评估方法

曾岚兰，闪鑫，王毅，王晨

（1.南瑞集团（国网电力科学研究院）有限公司，南京 211106；2.国电南瑞科技股份有限公司，南京 211106）

0 引言

随着国家“双碳”目标的不断推进，新能源发电占比逐步提高，其受季节、天气等因素影响表现出较大的随机性、间歇性，给电力系统的安全稳定运行带来严重影响［1-2］。电网中灵活的负荷侧调节资源成为平抑风光波动、响应新型电力系统调控需求的有效手段［3-4］。

目前国内外学者在负荷资源的响应潜力评估方面开展了大量研究。文献［5］根据电热转化原理对电采暖负荷进行建模，并根据其调节功率、电量和持续时间对电采暖的可调能力进行了评估。文献［6-7］分析了电动汽车参与电网调度的控制模式，分别给出了电动汽车上调和下调容量的计算方法。文献［8］以单个温控负荷的热力学模型为基础，进一步构建了居民温控负荷聚合模型，可有效求取典型居民温控负荷的响应潜力。从以上研究中可看出，目前对负荷侧响应潜力评估的研究大多集中于对用户的用电行为分析、对负荷进行精细化建模等方面。然而负荷侧资源的调度能力不但与设备本身运行特性相关，还受通信延迟、气候环境、用户市场行为特性等多方面因素影响，其响应潜力评估较为复杂［9-11］。另外，电网中负荷资源众多且运行状态参差不齐，在实际运行时，需要根据当前电网实际情况选取高响应潜力的资源进行调控才能高效发挥负荷资源的作用。获取全部负荷资源的精准响应量工作繁琐且难以取得效果，同时会造成不必要的人力和物力成本投入。目前，综合考虑各难以量化的影响因素，从宏观层面挖掘负荷资源响应潜力的研究较少。

为此，本文基于现有文献分析以及电网实际运行情况，从外部（经济、社会）和内部（负荷、系统特性）两个角度构建了负荷响应潜力的多维影响因素体系，包含12 个影响因素，旨在对计及多维影响因素下的负荷资源响应潜力进行充分挖掘。考虑到专家评估结果的主观性、差异性以及评估信息的有限性和模糊性，部分影响因素难以通过定量的形式精确表示。模糊数理论为处理此类模糊不确定数据的有效方法，本文将所有指标视为定性信息，并采用三角模糊数和梯形模糊数对影响因素中的定性信息进行表征［12］。确定指标常用方法有层次分析法［13］、灰色关联分析［14］、数据包络分析［15］、CRITIC（基于相关性的权重求取）方法和SWARA（逐步加权评估比率分析）等。SWARA是一种简单的主观权重确定方法，充分考虑了决策者针对指标优先级的偏好，在此基础上估计每个指标的相对重要性比率，能够有效获取指标权重，在供应商评估［16］和选择医疗药品综合评价［17］等方面皆有应用，但该方法不能客观描述各指标的重要性。CRITIC作为传统熵权法的改进，是一种基于指标所含信息量的客观赋权法，充分考虑了各指标之间的差异性和相关性［18］。影响负荷响应潜力的各因素之间往往具有一定的关联性，为了充分考虑此关联性带来的影响，本文将基于SWARA的主观权重和基于CRITIC的客观权重进行有效融合，对指标进行组合赋权，既考虑了专家的主观意见又融合了指标间的关联关系，为评估决策的合理性和可靠性提供有效保障。

负荷响应潜力评估还需借助多属性决策方法集结所有指标的评估信息，进一步确定最终的评估结果。文献［19］采用了MARCOS（基于折中方案的备选方案排序），通过定义备选方案与参考方案之间的关系，计算各备选方案的效用函数，并实现与理想方案和反理想方案相关联的折中排序。MARCOS避免了繁琐的计算，不需参数预设，并且还考虑了距离的相对重要性，与其他多属性决策方法相比具有更高的评估可靠性和准确性［20］。目前MARCOS在配电网风险识别、海上风电选址等方面已有广泛的应用［21-22］。

基于以上分析，本文提出一种基于SWARACRITIC-MARCOS的负荷侧资源响应潜力评估方法，旨在从宏观角度建立一个综合的群体决策框架，从多属性决策的视角出发，综合考虑经济、社会、负荷以及系统特性层面的影响因素，并基于模糊数理论将专家提供的评估信息进行语义转化，将模糊数应用于评估决策，通过模糊环境下的基于SWARA-CRITIC方法计算各项指标的主、客观权重信息，进一步求取综合权重，再通过MARCOS的多属性决策方法计算响应潜力的综合评估值。以上海市部分可调度用户负荷为算例基础，验证本方法的有效性。

1 影响因素指标构建

负荷响应潜力的评估属于典型的多属性决策问题。本文从负荷层面、经济层面、社会层面以及系统特性层面构建以下12 个负荷响应潜力的影响因素指标。

1.1 负荷层面

持续时间C11表示负荷在某一时间段内参与响应的可持续时长。参与响应的负荷的持续时间应满足电网的需求时间。

可中断和可转移负荷投入占比C12表示在该负荷集群可中断负荷和可转移负荷占所有负荷的比重。通常具有高可中断和高可转移负荷占比的负荷用户具有更高的响应潜力。

负荷重要性程度C13表示负荷的重要性。重要交通枢纽、医院等一级负荷需要更高的供电可靠性，一旦中断供电将产生重大社会、经济影响。因此，在负荷参与调度的过程中，具有高重要性的负荷往往响应潜力较低。

1.2 经济层面

用户响应损失C21表示负荷在响应过程中因实施负荷中断或负荷转移造成的经济损失。一般来说，响应损失大的负荷为避免严重的经济损失而具有较低的响应潜力。

经济激励水平C22表示当地政府对参与响应负荷的经济补偿。经济激励水平越高，越能提高负荷用户参与响应的意愿。

用户的经济效益C23表示用户经济水平的高低。在面对相同的经济激励政策时，C23越高的用户受激励的影响可能较小，响应意愿较低。

1.3 社会层面

用户社会影响度C31用来评价负荷对社会的影响程度。规模大的企业可带动周边地区的经济效益、解决就业等，对社会的影响程度相对较大。该类型企业参与负荷响应有可能会对周边地区产生影响，因而具有较小的响应潜力。

公众接受度C32表示周围民众对该负荷参与负荷响应的接受程度，周围民众接受程度越高，则响应潜力越高。

用户响应意愿C33高的电力负荷用户会更愿意接受电价激励政策，可能会通过适当改变生活方式、调换生产线、调休等方式参与响应，具有更高的响应潜力。

1.4 系统层面

系统运停切换难度C41表征整个可调节负荷系统在参与响应时进行负荷转移或者负荷中断的难度大小。例如，部分具有完整生产线的工业用户受工艺技术等因素的影响，系统运停切换的难度较大，而空调、照明等负荷可通过关闭或者调暗来进行响应，运停切换难度相对较小。

系统响应时间C42表示负荷接收到调度指令后，达到响应目标功率所需的时间。响应时间越短说明该负荷能更快速地响应，在实际运行中应优先考虑响应时间短的负荷参与响应。

系统管理水平C43较高的负荷用户可更加合理安排用电时间，规划生产计划，通常在参与响应时也会具有更短的响应时间和更高的响应准确性，因此具备更优的负荷响应潜力。

2 负荷响应潜力评估

本文结合模糊环境下SWARA-CRITIC 的权重计算方法和MARCOS多属性决策方法设计了负荷响应潜力评估框架，如图1所示。在第1章中已定义了12 个负荷响应潜力影响因素指标，指标集表示为Cj=(C1，C2，…，Cn)，j=1，2，…，n。假 设备选方案（即待评估负荷用户）有m个，备选方案集表示为Ai=(A1，A2，…，Am)，i=1，2，…，m，并有K名专家组成决策群体对以上备选方案进行评估，专家群体表示为Dk=(D1，D2，…，DK)，k=1，2，…，K。

图1 负荷响应潜力评估框架Fig.1 The framework for load response potential assessment

2.1 基于SWARA的主观权重获取

本文将SWARA 运用到模糊环境中来确定负荷响应潜力评估中影响因素指标的主观权重。各指标的重要性程度由决策者根据表1中所给出的语义变量进行评估获得，并根据表1中模糊标度转化为三角模糊数［23］。主观权重获取步骤如下。

表1 评估影响因素指标权重的语义变量及对应模糊标度Table 1 Semantic variables and the corresponding fuzzy scales for assessing indicator weights of influencing factors

步骤1：首先通过收集专家意见，按照表1中的语义变量对指标重要性进行评估。记专家k对指标j评估的语义变量为，对应的三角模糊标度为，j=1，2，…，n。

步骤2：获取K位专家对于指标权重的评估结果矩阵：

计算每个指标j的平均三角模糊数：

步骤4：从排序第二的指标开始计算指标j和前一个指标j-1间的差值cj，以确定每个指标得分的相对重要性。

步骤5：评估指标的相对系数rj：

步骤6：计算指标的修正权重值πj：

步骤7：计算各影响因素的主观权重αj：

2.2 基于CRITIC的客观权重获取

本文采用模糊环境下基于CRITIC 的方法求取客观权重，步骤如下。

步骤1：与采用SWARA方法相似，首先形成与式（1）相同的指标权重评估结果矩阵

步骤3：将标准化矩阵中每个元素的三角模糊进行去模糊化，计算其三角模糊清晰值［24］，如式（10）—（12）所示。

步骤4：求取标准化评估矩阵相关系数及标准差。

CRITIC方法用标准差来表示指标之间的对比度，并用指标之间的相关系数来量化冲突性，冲突性越高，指标之间关联性越低。每个指标之间的标准差σj及相关系数ρij通过式（13）与式（14）求取。

步骤5：计算客观权重βi。

由相关系数和标准差求取每个指标包含的信息量Ej。

当某个指标蕴含的信息量Ej越大，则它所占的权重也就越大。指标的客观权重βi表示为每个指标的信息量占所有信息量的比重。

2.3 综合权重的确定

在获取了每个指标的主观权重和客观权重后，本文采用线性加权方法将两部分权重进行结合确定综合权重wj。

式中：0<ζ<1，αj代表由SWARA方法求的指标j的主观权重，βj表示由CRITIC 方法求的指标j的客观权重。

2.4 基于MARCOS的多属性决策

在获得负荷响应潜力各个影响因素的数值以及对应权重后，还需要综合这些因素进行评估，但简单的线性加权方法难以保证评估结果的准确性。因此，本文将基于模糊环境下MARCOS的多属性决策方法与各影响因素指标相结合，实现对负荷响应潜力的综合评估。MARCOS的具体步骤如下［25］。

步骤1：在群体决策过程中，首先构建一个由m个备选方案和n个指标构成的初始群决策矩阵Am×n=[]m×n。由于本文所有影响因素均为定性因素，难以用清晰数进行准确的定量表示，因此需要专家根据表2所示的梯形模糊数及相应的模糊标度［26］，提供各备选方案在所有影响因素指标下的评估信息。

表2 评估方案的语意变量及其对应的模糊标度Table 2 Semantic variables and the corresponding fuzzy scales of the assessment scheme

将由评估信息矩阵Am×n与由式（17）求出的各指标的权重相乘，计算加权决策矩阵：

步骤2：构建扩展的加权决策矩阵。在这一步中，在式（19）的矩阵中加入AI（理想解矩阵）和AAI（反理想解矩阵）来实现初始决策矩阵的扩展，具体如式（20）所示。

式中：AI=[xaj]1×n且AAI=[xaaj]1×n。表示针对指标Cj的理想值，表示针对指标Cj的反理想值，即矩阵AI代表每个指标下性能最佳的方案，AAI代表每个指标下性能最差的方案。

式中：B代表效益型指标；C代表成本型指标。

步骤3：利用式（23）对初始矩阵Xm×n进行规范化，生成规范化矩阵N=[]m×n。

步骤4：计算各个方案的效用度Ki。

步骤5：根据各方案的效用度和相关效用函数计算各个方案的最终效用函数f(Ki)：

式中：f()为与AI有关的效用函数；f()为与AAI有关的效用函数，如式（27）和式（28）所示。

步骤6：根据式（26）—（28）求出的效用函数值大小并进行排序，得到不同负荷响应潜力的最终评估结果。

3 算例及结果分析

3.1 算例

选取上海市钢铁企业、水泥行业、电子元件行业、大型商场4 类电力用户，采用本文所提的SWARA-CRITIC-MARCOS 方法对2023 年5 月某一典型工作日下用电高峰时期（14：00）的4 类电力用户（A1—A4）进行负荷响应潜力评估。评估信息分别由来自政府、电网调度、电网运营和电网营销部门的4 位专家（D1—D4）给出。首先要获取影响因素指标权重评估信息以及方案评估信息。专家根据表1中的语义术语，结合自身经验及专业对12 个影响因素指标在负荷响应潜力评估中的重要性进行评价，形成影响因素指标权重的初始评估矩阵如表3所示。另外，4位专家还需要根据表2的语义信息对4类电力用户在12个影响因素指标下的性能进行评估，得到初始决策矩阵，如表4所示。

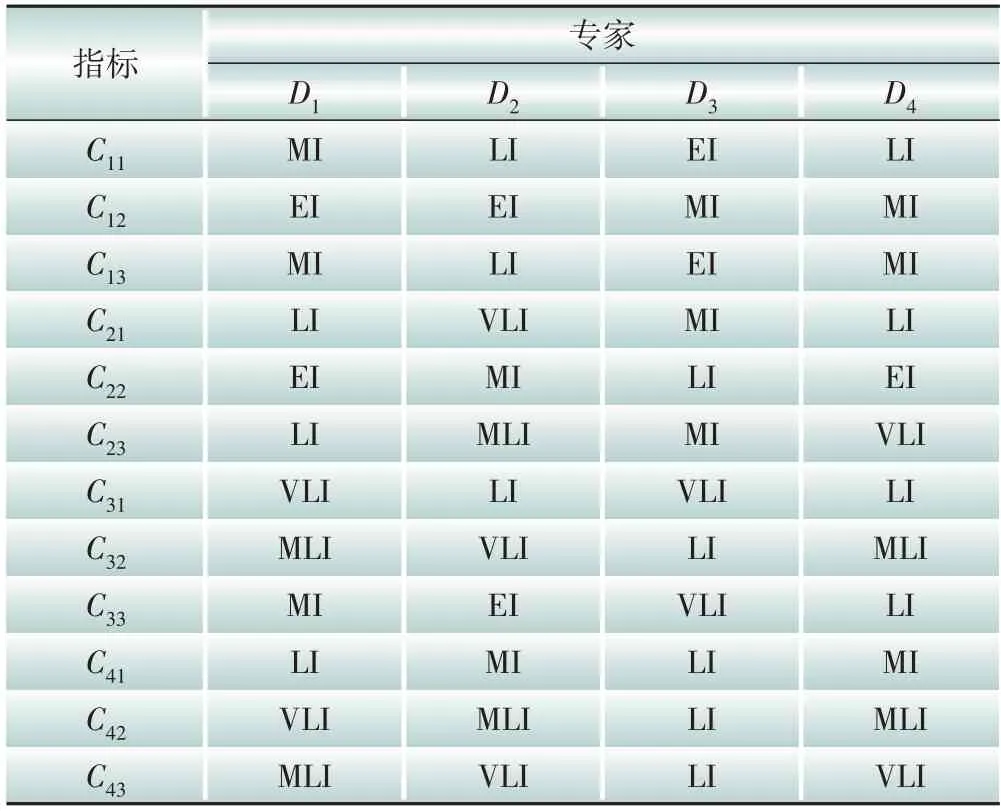
表3 初始评估矩阵Table 3 The initial evaluation matrix

表4 初始决策矩阵Table 4 The initial decision matrix

采用SWARA 方法计算各影响因素指标的主观权重。根据表1中的对应关系，表3中的评估数据可进一步量化为三角模糊数，由式（2）计算每个影响因素指标权重的平均三角模糊数，并结合式（3）获得各清晰值。进一步地，根据式（5）—（7）计算各影响因素的相对系数、修正权重值和最终权重计算结果如表5所示。

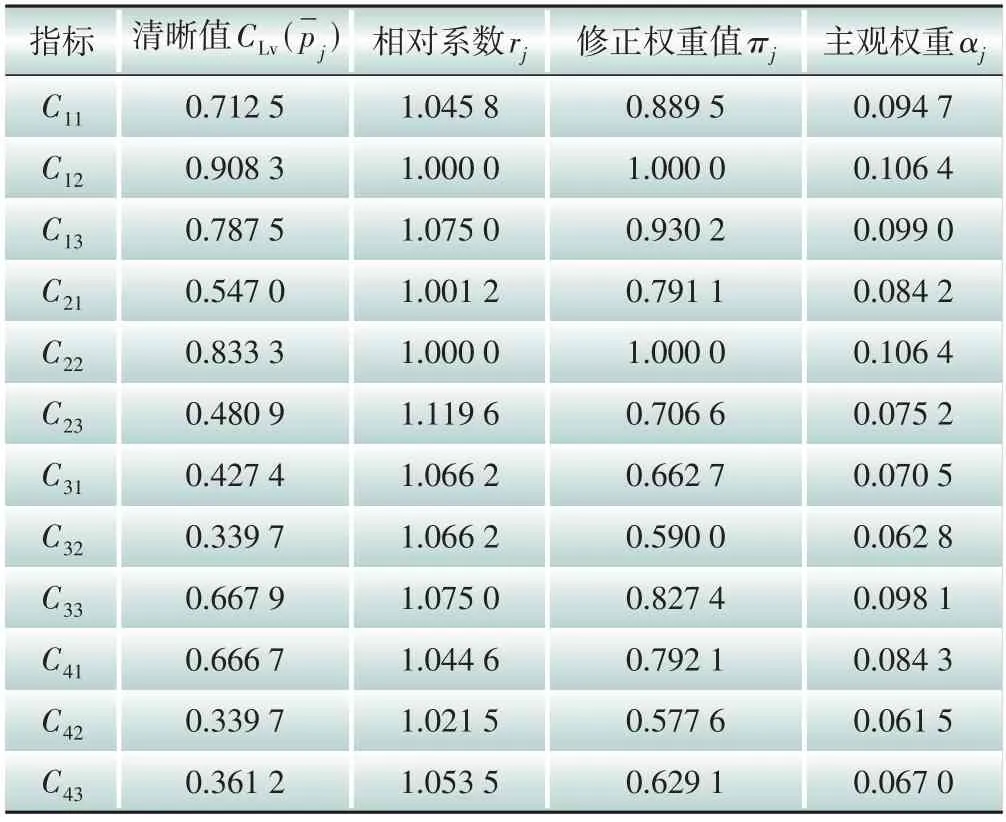
表5 基于SWARA方法计算的各指标清晰值、相对系数、修正权重值和主观权重Table 5 Clear values，relative coefficients，adjusted weights and subjective weights of each index based on the SWARA method

考虑到基于SWARA 方法的主观局限性，本文采用CRITIC方法获取客观权重。根据表3中的初始评估矩阵以及式（8）—（16）得到针对每个指标的信息量Ej和客观权重βj，计算结果如表6所示。

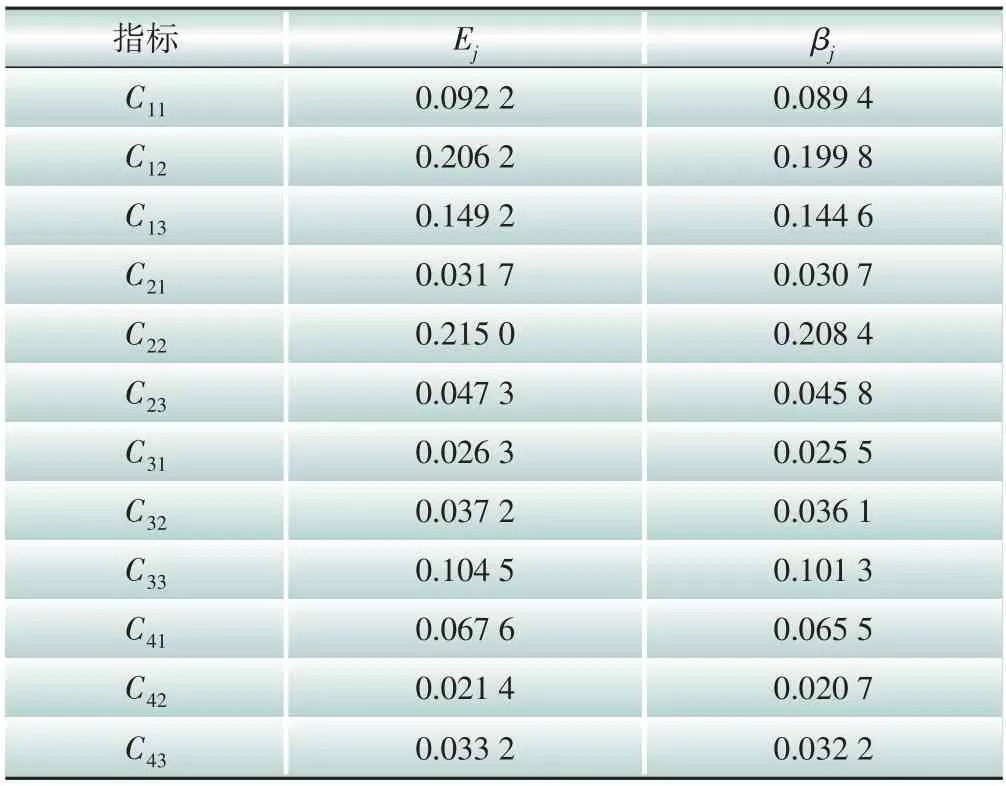
表6 基于CRITIC方法的各指标信息量及客观权重Table 6 Information values and objective weights for each indicator based on the CRITIC method

将基于CRITIC 的客观权重和基于SWARA的主观权重进行线性加权，本文令式（17）中的参数ξ=0.5，即认为主、客观权重的重要性为同等程度，得到的各影响因素指标综合权重如图2所示。

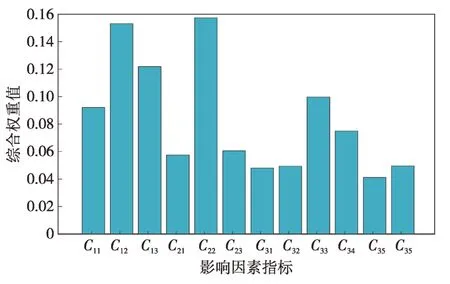
图2 各影响因素指标的综合权重Fig.2 The comprehensive weights of the impact factor indicators

计算各影响因素的权重后，采用基于MARCOS的方法结合各指标对负荷响应潜力进行评估。首先，构建如表4所示的初始决策矩阵，与已求出的综合权重结合可得到加权的决策矩阵。接着，分析12个影响因素的属性，其中C13、C21、C23、C31、C41、C42为成本型指标C，即该指标越低，用户负荷响应潜力越高，对应的其余指标为效益型指标B。根据式（21）—（22）可以得到每个影响因素下的理想解与非理想解，将AAI与AI引入加权矩阵得到扩展决策矩阵。根据式（23）将加权矩阵进行规范化生成规范化矩阵如表7所示。

表7 规范化后加权矩阵Table 7 The normalized weighted matrix

由此，采用式（24）—（28）计算各电力用户负荷响应潜力的效用函数值，结果如表8所示。

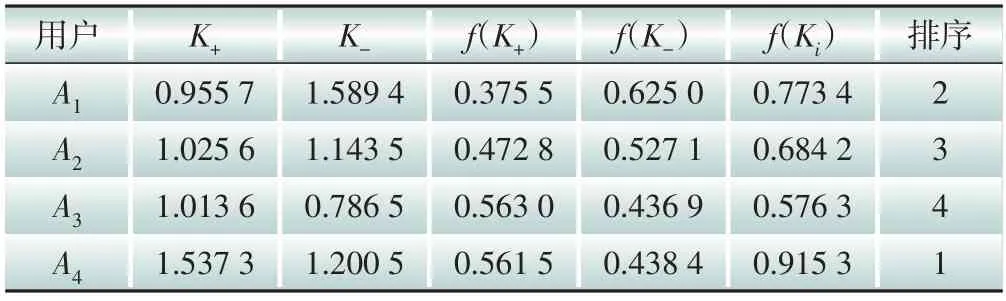
表8 用电高峰时各电力负荷响应潜力评估的效用函数值及排序结果Table 8 The utility function values for power load response potential assessment during peak consumption period and the ranking results

根据以上结果，可以得到用电高峰时期4类负荷的响应潜力排序为：A4>A1>A2>A3，即A4负荷用户的响应潜力最高，A3的响应潜力最低。结合实际情况分析，A4为大型商场，商场属于公共设施类用电负荷，用电主要以空气调节系统和照明负荷为主，同时空气调节系统和照明用电可以作为可中断负荷通过温度以及亮度调节参与需求响应管理，系统运停切换难度小、响应时间短、负荷重要性等级较低，在夏季高峰时期响应比较灵活，成本相对较低，能够在不影响用户舒适度的情况下参与响应。A3为电子元件制造企业，其负荷在8：00—11：00和14：00—16：00会出现峰值，需要更大的激励措施，且电子元件制造企业涉及精密仪器，响应成本可能较高。此外，A1和A2分别为钢铁企业和水泥企业，钢铁企业中轧钢生产线具有可中断潜力，生产的灵活性较高，具有良好的避峰潜力，在面对合理的经济激励政策时，此类负荷为了降低生产成本也可能参与需求响应，减轻系统供电压力。水泥企业大部分负荷属于二级负荷，且水泥行业设备运转周期较长，总体负荷曲线的波动小，但处于生产淡季时可参与的可中断负荷较大，可中断响应潜力高。

为了验证本文所提出的负荷响应潜力研究框架在不同用电情况下评估的有效性，以2023 年5月某一典型工作日用电低谷时（06：00）为例，与用电高峰时段的评估过程类似，对以上4类电力用户（A1—A4）的响应潜力进行评估。所得的各电力负荷响应潜力评估的效用函数值及评估结果如表9所示。

表9 用电低谷时各电力负荷响应潜力评估的效用函数值及排序结果Table 9 The utility function values for power load response potential assessment during valley consumption period and the ranking results

由评估结果可以看出，在用电低谷时期，4类负荷的响应潜力评估结果与用电高峰时期略有不同，排序结果为：A1>A4>A3>A2，产生区别原因可能为在用电低谷时期，钢铁企业与大型商场均具有较大的响应潜力，而钢铁企业的响应较集中，单位用户的执行容量更大。且这时候电子元件制造行业用电负荷曲线不处于高峰值，相比于负荷曲线波动较小的水泥行业具有更高的响应潜力。

3.2 对比分析

为了验证本文所提方法的有效性与可行性，重新选取了3 种典型的多属性决策方法，TODIM（交互式多属性决策方法）［27］，TOPSIS（逼近理想解排序法）［28］以及VIKOR（变权多准则优化妥协决策）［29］。

为便于比较，采用相同的评估环境以及赋权方法，以上方法简称为SWARA-CRITIC-TODIM方法、SWARA-CRITIC-TOPSIS 方法以及SWARA-CRITIC-VIKOR方法，采用以上3种方法与本文所提的SWARA-CRITIC-MARCOS 方法进行对比分析。SWARA-CRITIC-TODIM 方法基于前景理论的价值函数，将备选方案进行对比并建立各方案的优势度函数Ψi，根据优势度的大小对方案进行择优［27］。在SWARA-CRITICTOPSIS 方法中，通过计算各个方案与正理想解以及负理想解之间的加权欧式距离，进一步计算各方案与最优方案之间的接近系数CCi作为评价方案的优劣标准，接近系数的方案为最优方案［28］。SWARA-CRITIC-VIKOR 方法依据正理想解与负理想解计算每个方案的群体效应指数、个体遗憾值以及总体适应指数Qi，总体适应指数越小，代表方案更为优越［30］。采用不同方法对用电高峰时期4类用户的响应潜力进行评估，得到的比较结果如表10所示。

表10 采用不同决策方法评估结果对比Table 10 Comparison of the assessment results obtained using different decision-making methods

从SWARA-CRITIC-TODIM 的计算结果可看出，4类电力负荷的响应潜力排序结果为：A4>A1>A2>A3，与本文所提的方法计算结果一致，并且所有方法均认为A3具有最低的响应潜力，由此可验证本文所提方法的有效性及可行性。在应用SWARA-CRITIC-TOPSIS 方法时，A4和A1之间的排名与其他三种方案不同，但总的来说，这4 种方法都认为A4的响应潜力在所有负荷资源中排在前两位。而之所以造成评估结果的不同，是因为TOPSIS 方法更依赖于每个备选方案与理想方案和负理想方案之间的距离（和），并且只对它们进行简单的加权计算，而没有考虑它们之间的相对重要性，因此容易导致逆序问题的发生［31］。与负荷A4相比，A1的较小而较大由此导致A1>A4结果。而MARCOS 方法考虑了备选方案与理想和反理想解之间的关系，实现与理想方案和反理想方案相关联的折中排序，从而很好地消除了上述TOPSIS 方法的缺点，提高了评估方法的可靠性和稳定性［25］，使SWARA-CRITICMARCOS得到的评估结果更为合理。在SWARACRITIC-VIKOR 方法下，A1与A2评估结果发生了交换，两种方案的总体适应度较为接近，这是因为决策环境对VIKOR方法的影响最为显著，难以有效区分两种方案的差异性，但对其他备选方法的评价结果也与本文所提方法保持一致。

通过上述不同评估方法的比较实验，可以得出本文提出的SWARA-CRITIC-MARCOS 决策框架在实际应用中是有效和可靠的。

4 结论

本文针对负荷侧资源响应潜力评估问题开展研究，从宏观层面构建了负荷响应潜力的多维影响因素体系。将模糊数理论应用于本文的方法中，采用SWARA-CRITIC 方法对各影响因素的主、客观权重进行求取，利用线性加权获取综合权重，采用MARCOS综合各影响因素对负荷响应潜力评估与排序。结合理论与案例分析，主要结论如下：

1）根据不同用电时段下，钢铁企业、水泥行业、电子元件行业、大型商场4类负荷响应潜力的评估情况，同时，选取另外3种典型的多属性决策方法与本文所提方法进行了对比分析，验证了本文提出的影响因素指标体系的合理性以及基于SWARA-CRITIC-MARCOS 方法的有效性和可行性。

2）针对传统响应潜力评估方法中单纯考虑负荷自身特性制定评估方案的不足，本文从宏观层面构建了负荷、经济、社会和系统层面的多维影响因素体系。并采用SWARA-CRITIC 方法从主观与客观的角度对各影响因素指标的重要性程度进行了精细化计算，全面考虑了各因素对负荷响应潜力的影响。

3）利用SWARA-CRITIC-MARCOS 方法可计算出各负荷的响应潜力效用函数值，并根据效用函数值的大小有效感知各负荷资源的响应潜力并进行排序，有助于调度人员对各负荷资源的响应潜力进行整体感知及负荷优选，优化了负荷资源配置，充分挖掘负荷的响应潜力。本文所提出框架也为群体决策环境下建模、评估提供了一个可行的视角，并为其他领域的研究提供参考。

本文采用线性加权法获取综合权重，后续研究中可探索更科学有效的综合权重计算方法，以保证获取的综合权重更可能地接近主观和客观权重，降低误差，使计算结果更加科学合理。另外，本文着重于从宏观角度进行分析，缺乏从微观角度的动态响应潜力评估。下一步工作将结合时间尺度特点对负荷的响应潜力进行更深入的研究，以获得更具体、精细化的结果。