一次函数图像是一条直线

函数图像是认识函数的重要工具，借助函数图像我们可以进一步研究函数。那么，如何画出一个一次函数图像呢？

我们知道函数图像是由一个个符合条件的点构成的，用描点法画出函数图像就是经历“列表、描点、连线”的三个步骤。现在有很多的数学软件工具可以帮助我们更加精确地画出图像，如网络画板、几何画板、GGB等动态几何软件。今天，我们就用网络画板来画一次函数的图像。

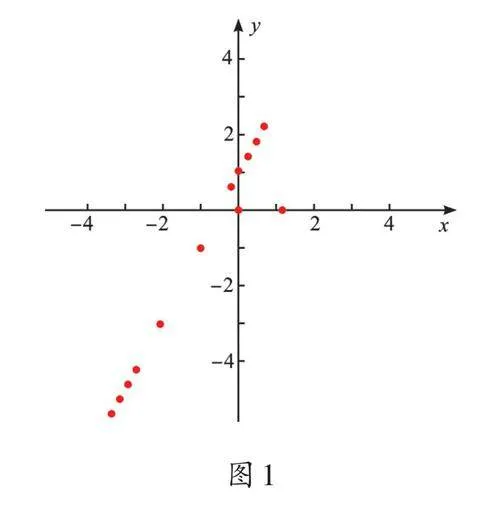
打开网络画板，建立平面直角坐标系，先描出以一次函数y=2x+1的对应值为坐标的若干个点，如图1。观察这些点，我们发现，这些点好像在一条直线上，但这些不足以说明一次函数的图像就是一条直线。因此，我们需要取更多对应的x、y值，并在平面坐标系中构造这些点，观察这些点的分布情况，发现都在这条直线上，由此，坚定我们的猜想：一次函数y=2x+1的图像可能是一条直线。

如图2，在x轴上构造一个点X，记横坐标为x，绘制动点P（x，2x+1）；移动点X，观察点P经过的路径，发现它是一条直线。

我们再任意给一个一次函数，用自己的方法画出它的图像，发现仍然是一条直线。

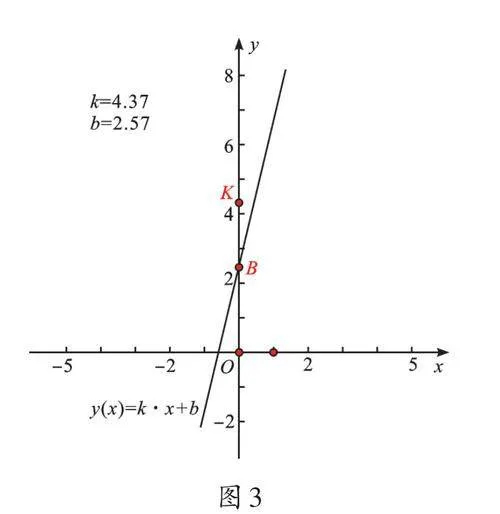
进一步建立直角坐标系，在y轴上构造点K、B，分别记它们的纵坐标为k、b，画函数y=kx+b的图像，如图3。移动点K，观察函数y=kx+b图像发生的变化，再移动点B，观察函数y=kx+b图像发生的变化。经过这样的探究，我们可以得到“一次函数的图像是一条直线”。当然，到九年级时，我们就可以自己证明这个结论了。

函数图像是研究函数的基础，初中阶段主要借助图像直观认识函数性质。函数内容中，一次函数具有奠基作用，仅凭在直角坐标系中描出几个点，就得出“一次函数图像是一条直线”的结论，缺乏可信度。借助动态几何软件，也可以是图形计算器，通过描点、加密点、跟踪点，探索一次函数对应值为坐标的点的分布规律，可以更加直观、一般地得出“一次函数的图像是一条直线”的结论。

（作者单位：江苏省盐城市毓龙路实验学校）