学好“一次函数”的必备攻略

领 "衔 "人：姜鸿雁（江苏省特级教师）

组稿团队：江苏省无锡市初中数学名师工作室

同学们，你知道吗，函数被德国著名数学家克莱茵称为数学的“灵魂”，可见它的地位和价值至关重要。学完“一次函数”之后，有的同学感到些许迷糊，甚至觉得有点难。那我们就一起来看看学好一次函数的几条必备“攻略”吧。

攻略一：明晰概念，经历数学抽象，认识数学模型

函数研究的是一个变化过程中两个变量x、y之间的关系，当变量x取一个值，变量y有唯一值与它对应。函数是从“常量数学”到“变量数学”的跨越，必然进入另一番天地。函数是一个“庞大的家族”，我们从最基本、最简单的一次函数开始学习，它的定义是：形如y=kx+b（k、b是常数，k≠0），y是x的一次函数。它就在我们的生活中，比如：

（1）一辆汽车的油箱中现有汽油5L，加油枪平均加油量为6L/min，那么油箱中的油量y（L）与时间x（min）之间的函数表达式为y=6x+5；

（2）某水库的水位在5h内持续上涨，初始水位高度为6m，水位以每小时0.3m的速度上升，则该水库的水位高度y（m）与时间x（h）之间的函数表达式为y=0.3x+6；

（3）某登山队大本营所在地的气温为30℃，海拔每升高1km，气温下降6℃，登山队员所在位置的气温y（℃）与海拔x（km）之间的函数表达式为y=-6x+30。

透过现象看本质，这些实际问题反映的等量关系都是：新值=均匀变化部分+初始值，因此可以抽象出y=kx+b（k≠0）这个数学模型来描述共性。

攻略二：研究图像，体会数形结合，培养几何直观

一次函数的图像是一条直线，以此表达“均匀变化”的特质，其图像位置由k和b决定。我们可以用“控制变量法”来理解。

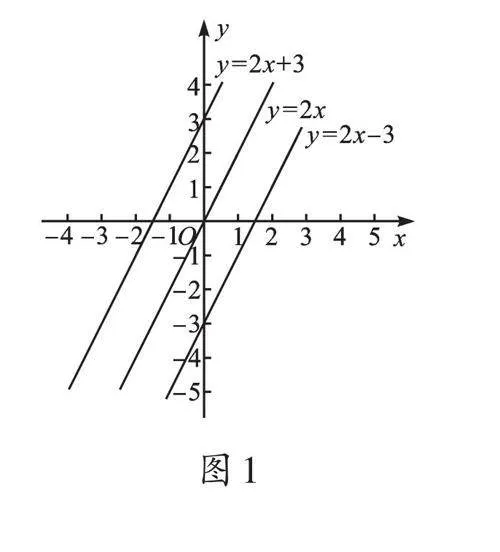
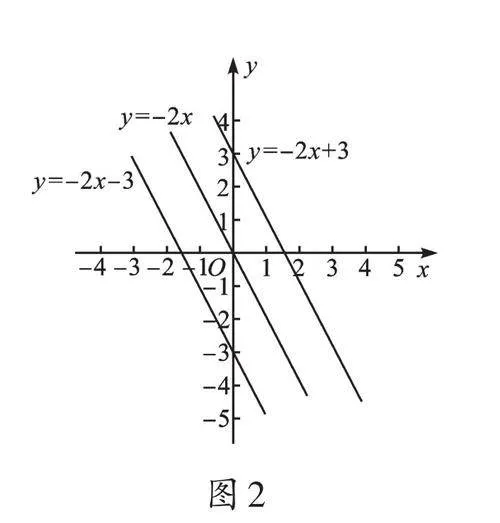
设k=2（如图1），随着b的变化，图像的位置发生变化，但相互平行；当k=-2时（如图2），也是如此。对比图1、图2可知，k值影响图像走势：当k＞0时，y随x的增大而增大（上升），必过第一、三象限；当k＜0时，y随x的增大而减小（下降），必过第二、四象限。

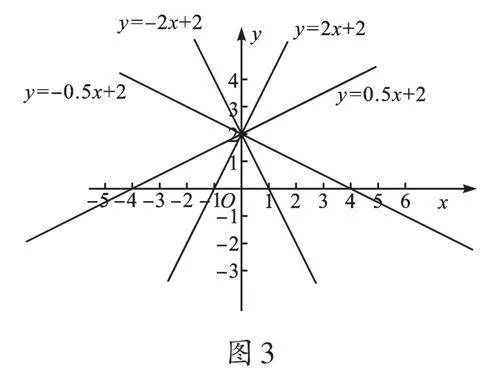
再设b=2（如图3），随着k的变化，图像与y轴的公共点始终为（0，2）。

可见，k、b的取值与图像的位置建立了联系。例如，若一次函数y=kx+k+1的图像不经过第三象限，求k的取值范围。这里要注意，“不经过第三象限”指经过第一、二、四象限或经过第二、四象限和原点。此类问题都只需画出草图，以形助数，故此题答案为-1≤k＜0。

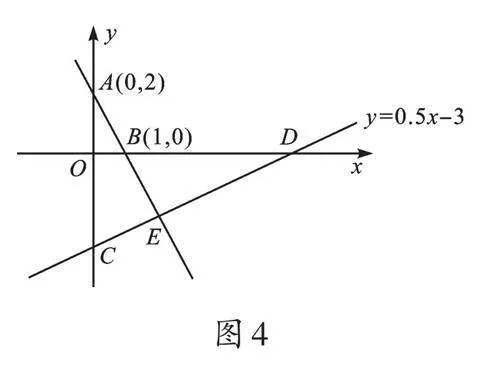
借助数形结合，我们还可以进一步研究如下问题。如图4，观察图像的信息，可求直线AB的函数表达式和点C、D坐标，联立两个表达式还可以求出点E坐标；利用图像法能求出不等式-2x+2＞0.5x-3的解集；还可求出△BED的面积……

通过研究一次函数图像，我们可以深入理解它的性质，深度剖析它与方程、不等式之间的关系，培养几何直观的能力。

攻略三：回归生活，体验建模过程，实现问题解决

函数源自生活，回归生活。在实际生活中，一次函数一直发挥着它的应用价值。

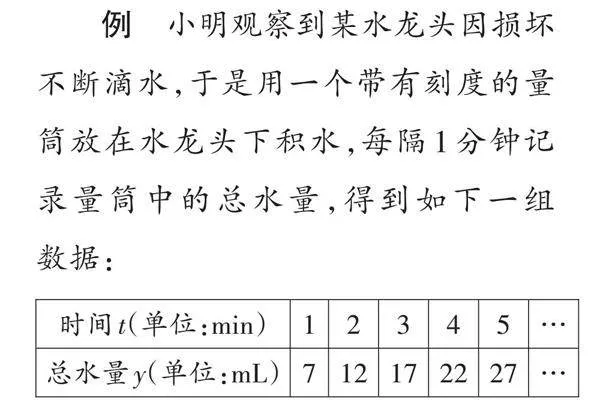
例 小明观察到某水龙头因损坏不断滴水，于是用一个带有刻度的量筒放在水龙头下积水，每隔1分钟记录量筒中的总水量，得到如下一组数据：

（1）开始计时时，量筒中有水吗？

（2）20分钟时，量筒中的水量是多少mL？

（3）一个人一天大约饮用1500mL水，估算这个水龙头一个月（按30天计）的漏水量可供一人饮用多少天。

观察表格发现，前后一分钟都相差5毫升水，具有“均匀变化”特质，故建立一次函数模型：y=kt+b（也可以把一组组值作为点的坐标，在平面直角坐标系中描出，观察函数图像），用待定系数法求出表达式y=5t+2；令t=0，y=2（mL）；令t=20，y=102（mL）；1个月的总滴水量：30×24×60×5=216000（mL），再得天数：216000÷1500=144（天）。真是不算不知道，一点一滴皆重要！

同学们，以上“攻略”沿着“概念、图像与性质、实际应用”的路径展开，这也是学习函数的一般路径，为日后学习其他类型的函数积累经验。一次函数仅仅打开了函数的大门，里面有非常广阔的天地任我们驰骋，让我们一起慢慢细品这一“数学之魂”吧！

（作者单位：江苏省宜兴外国语学校）