有趣的坐标系

平面直角坐标系是一种重要的数学工具，它可以帮助我们确定地理位置，是“数”与“形”之间的桥梁，还可以帮助我们直观、形象、简明地解决许多问题。在现实生活中还有多种坐标系，今天我们来简单认识一下它们。

“菱形”坐标系

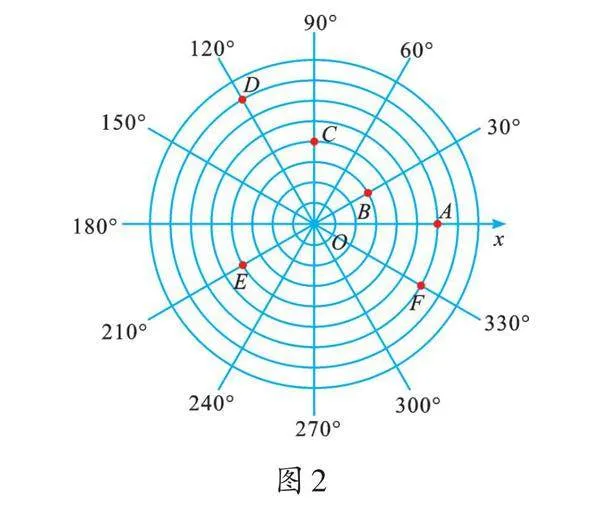
类似于平面直角坐标系，在平面内画两条原点重合、单位长度相同的数轴，但夹角非90°，仍然记这两条数轴为x 轴、y轴；过每一刻度点分别画平行于x 轴、y 轴的直线，每条相交的直线将平面分成若干个小菱形。这样的坐标系称为“菱形”坐标系。

如图1，在“菱形”坐标系中，原点O 的坐标表示为（0，0），点A 的坐标表示为（4，0），点C 的坐标可表示为（-3，2）。同样，我们能写出图中点B和点D 的坐标。

“圆”坐标系

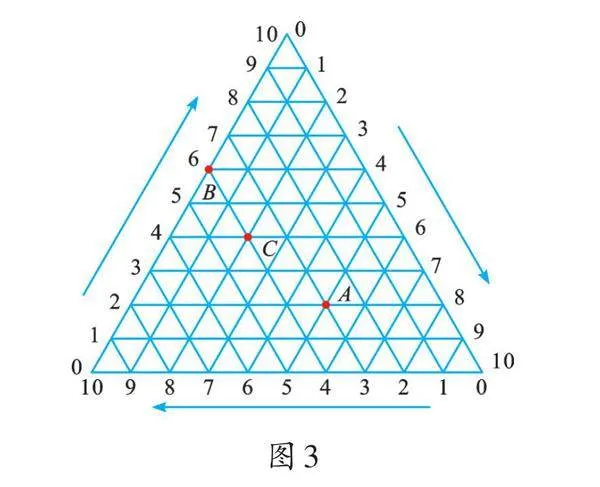
画一条水平数轴，以原点O 为圆心，过数轴上的每一刻度点画同心圆，过原点O 按逆时针方向画与数轴正半轴的角度分别为30°、60°、90°、120°、150°……330°的射线，这样就建立了“圆”坐标系。

如图2，在“圆”坐标系中，我们可以将点A、B、E的坐标分别表示为A（6，0°）、B（3，30°）、E（4，210°）。同样，我们也能写出图中点C、D、F 的坐标和在图中找到点G（6，120°）、H（2，300°）、I（4，135°）。

“三角形”坐标系

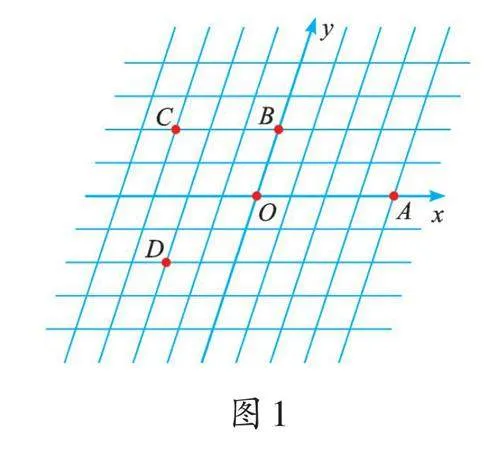
将一个等边三角形的三条边分成10等分，按顺时针方向（图中箭头方向）标注端点及各等分点的序号0、1、2、3、4、5、6、7、8、9、10，将不同边上序号和为10的两点依次连接起来，这样就建立了“三角形”坐标系。

如图3，在“三角形”坐标系中，每一点的坐标用过这一点且平行（或重合）于原三角形三条边的直线与三条边交点的序号来表示（水平方向开始，按顺时针方向），如点A的坐标可以表示为（2，5，3）。同样，我们能写出图中点B、C 的坐标。观察 A、B、C 三点的坐标，你有什么发现？

坐标系是为了描述物体的位置而建立的参考系，但它的作用远不止于此。在未来的学习中我们会发现，通过坐标系中点的坐标表示，可以将代数问题与几何问题互相转化，从而解决问题。坐标系的应用，推动了微积分等现代数学的发展，我们必须掌握各种坐标系对点的位置的表述规则，才能科学地研究各种几何对象的数学性质。

（作者单位：江苏省盐城市毓龙路实验学校）