钢箱梁桥设计验算时第一体系与第二体系叠加的问题分析
2024-05-15王翰珣合肥市市政设计研究总院有限公司安徽合肥230001
王翰珣 (合肥市市政设计研究总院有限公司,安徽 合肥 230001)
1 钢箱梁的传力体系
随着我国城市化进程不断加速,经济不断发展,对基础设施建设特别是市政及交通建设的需求日益增加。桥梁工程,特别是大型及特大型桥梁工程在其中发挥着重要的节点作用,而对于大跨径桥梁,在工程材料短时间没有突破性研究进展的情况下,钢结构是目前公认的最优选择。
《钢桥》《桥梁工程》《现代钢桥》是国内高校及业界主流的教材,均将钢桥面板分为三个基本结构体系。
Ⅰ:由顶板和纵肋组成的结构系,是主梁的一个组成部分,与主梁共同受力,称为主梁体系。
Ⅱ:由纵肋、横肋和顶板组成的结构系,顶板被看成纵肋、横肋上翼缘的一部分。结构系Ⅱ起到了桥面系结构的作用,把桥面上的荷载传递到主梁和刚度较大的横梁,称为桥面体系。
Ⅲ:把设置在肋上的顶板看成是各向同性的连续板,这个板直接承受肋间的轮荷载作用,同时把轮荷载传递到肋上,称为盖板体系。
在荷载作用下,钢桥面板任何一点的内力可由上述三个基本结构体系的内力适当叠加而近似地求出,其中体系Ⅲ根据多次实验证实可以忽略不计。
2 国内外行业规范的验算要求
我国目前现行的《公路钢结构桥梁设计规范》(JTG D64-2015)及《铁路桥梁钢结构设计规范》(TB10091-2017)中关于受弯构件的验算,均未对上述的钢桥面板的结构体系Ⅰ、Ⅱ如何叠加进行论述解释,仅针对体系Ⅲ提出了桥面板变形验算要求(第8.2.5条)。
《公路常规跨径钢结构桥梁建造技术指南》要求考虑上述的三个结构体系,但未明确如何对三个结构体系进行叠加验算。而《公路钢桥面铺装设计与施工技术规范》(JTG/T 3364-02-2019)则针对体系Ⅲ的桥面板变形验算给出详细的验算要求。
日本规范直接叠加体系Ⅰ与体系Ⅱ的结果,通过将材料允许值提高40%来考虑体系之间的相互作用。
欧洲规范采用体系Ⅰ取max+0.7×体系Ⅱ取max;0.7×体系Ⅰ取max+体系Ⅱ取max 两种情况中更不利的一种作为验算标准。
3 精细化(板壳)模型结果与单梁验算方式的对比
由于目前我国规范对钢桥面板的两种体系缺乏相应的验算标准规定,在实际工程中,钢桥面板构件的设计验算往往由各设计院或钢结构生产机构自行确定相应标准。因此本文针对某一实际工程项目进行桥面板设计验算的对比,提出两种体系的叠加验算方法。
3.1 主梁设计资料
主梁采用单箱单室闭口截面,全宽9.0m,高1.9m,跨径为单跨40m 简支梁,材料采用Q345qD。顶板厚度采用16mm,底板厚度采用20mm,腹板厚度采用16mm。顶板翼缘板与底板的加劲肋采用190mm×16mm 板肋,腹板加劲肋采用160mm×14mm 板肋,顶板箱内加劲肋采用U-2(桥梁钢结构用U 形肋冷弯型钢YB/T 4624-2017)型闭口U肋。翼缘板下横隔板按顺桥向2m 间距布置,实腹式横隔板和框架式横隔板均按顺桥向4m 间距布置。支座横桥向间距4.8m,对称布置。
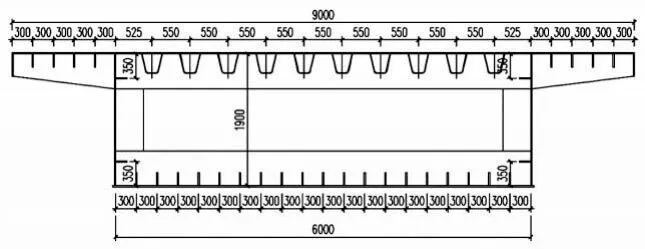
图1 主梁典型断面
3.2 模型概况
建模采用Midas Civil(2021 版)有限元软件建立计算模型。为确保模型的标准统一,先建立板壳单元模型,后验算其结构自振频率及自重恒载反力,再建立单梁模型并根据板壳单元模型的自振频率和恒载反力分别对其汽车荷载冲击系数及自重系数进行修正。为方便核查结果,活载仅设置车道荷载,采用城-A级,两车道左偏布载。
3.2.1 主梁单梁模型
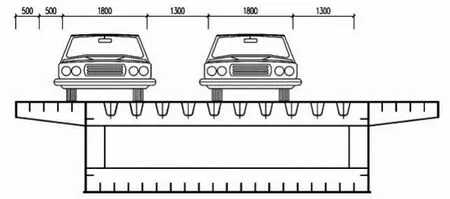
图2 车道布载示意
模型共计采用41 个节点、40 个单元。单元截面为顶、底、腹板及其纵向加劲肋,不含横隔板。截面有效宽度考虑剪力滞效应及局部受压稳定的折减,见图3。
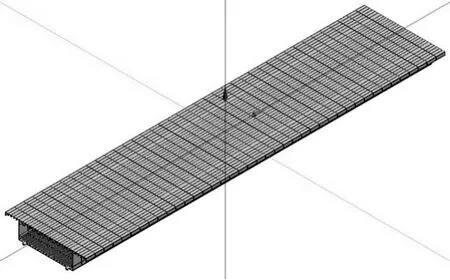
图3 结构离散模型
①自重恒载下的反力结果
自重恒载作用下的主梁每个支座竖向反力均为443053.0N,即梁的自重为1772212.0N(180.8t),显示单梁模型的外部边界条件模拟较为可靠,与板壳单元计算结果基本一致,见图4。
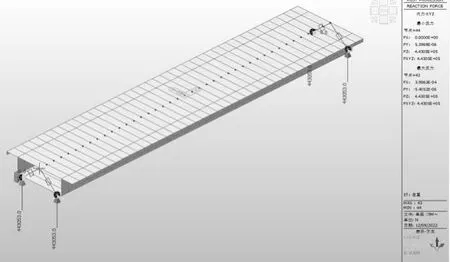
图4 自重恒载反力图(单位:N)
②自重恒载下的内力(纵向弯矩My)结果
自重恒载作用下的主梁标准组合内力(弯矩)结果显示简支梁跨中处正弯矩最大为8861.1kN·m,内力分布规律符合简支梁受力特性,见图5。
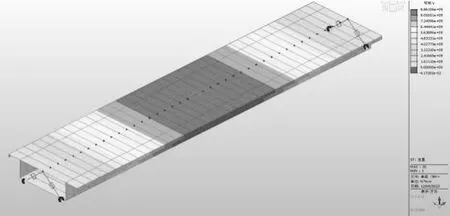
图5 自重恒载内力图(单位:N·mm)
③自重恒载下的应力结果(顶板)
自重恒载作用下的主梁标准组合跨中顶板最大压应力为21.9MPa,应力分布规律符合简支梁受力特性,见图6。
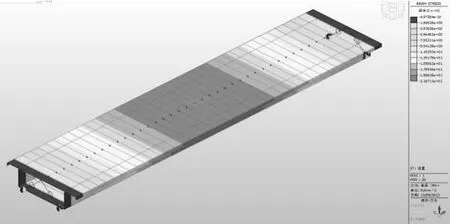
图6 自重恒载应力图(单位:MPa)
④汽车活载下的反力结果
汽车活载作用下的主梁偏载一侧的两个支座竖向反力为1078440.5N,另一侧两个支座竖向反力为543909.2N,显示单梁模型的外部边界条件模拟较为可靠,与板壳单元计算结果基本一致,见图7。
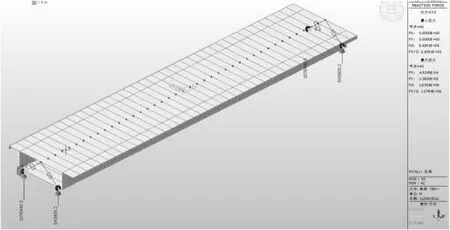
图7 汽车活载反力图(单位:N)
⑤汽车活载下的内力(纵向弯矩My)结果
汽车活载作用下的主梁标准组合内力(弯矩)结果显示简支梁跨中处正弯矩最大为1335.3kN·m,内力分布规律符合简支梁受力特性,见图8。
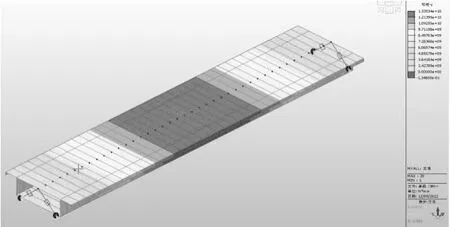
图8 汽车活载内力图(单位:N·mm)
⑥汽车活载下的应力结果(顶板)
汽车活载作用下的主梁标准组合跨中顶板最大压应力为33.5MPa,应力分布规律符合简支梁受力特性,见图9。

图9 汽车活载应力图(单位:MPa)
3.2.2 板肋单梁模型
模型共计采用41 个节点、40 个单元。单元截面为190mm×16mm 板肋及布置间距300mm 的主梁翼缘顶板。截面有效宽度考虑剪力滞效应及局部受压稳定的折减。板肋与横隔板连接处采用全固结支座模拟,汽车荷载采用车辆荷载(城A),考虑到模型结构的截面宽度为300mm,根据规范,单个车轮的宽度为600mm。因此该模型的汽车荷载横向分布系数采用0.5×300/600=0.25,冲击系数按局部加载取0.4,见图10、图11。

图10 结构离散模型

图11 单元截面(单位:mm)
①自重恒载下的反力结果
自重恒载作用下的主梁支座竖向反力合计为24617.6N,即梁的自重为2.5t,显示单梁模型的外部边界条件模拟较为可靠,见图12。

图12 自重恒载反力图(单位:N)
②自重恒载下的内力(纵向弯矩My)结果
自重恒载作用下的主梁标准组合内力(弯矩)结果显示主梁跨中处正弯矩最大为102573.3N·mm,中支点处负弯矩最大为205146.7N·mm,内力分布规律符合连续梁受力特性,见图13。

图13 自重恒载内力图(单位:N·mm)
③自重恒载下的应力结果(顶板)
自重恒载作用下的主梁标准组合支点顶板最大拉应力为0.5MPa,应力分布规律符合连续梁受力特性,见图14。

图14 自重恒载(顶板)应力图(单位:MPa)
④自重恒载下的应力结果(底板)
自重恒载作用下的主梁标准组合支点底板最大压应力为1.3MPa,应力分布规律符合连续梁受力特性,见图15。

图15 自重恒载(底板)应力图(单位:MPa)
⑤汽车活载下的反力结果
汽车活载作用下的主梁支座竖向反力结果显示单梁模型的外部边界条件模拟较为可靠,见图16。

图16 汽车活载反力图(单位:N)
⑥汽车活载下的内力(纵向弯矩My)结果
汽车活载作用下的主梁标准组合内力(弯矩)结果显示主梁跨中处正弯矩最大为14.7kN·m,中支点处最大负弯矩为17.3 kN·m,内力分布规律符合连续梁受力特性,见图17。

图17 汽车活载内力图(单位N·mm)
⑦汽车活载下的应力结果(顶板)
汽车活载作用下的主梁标准组合支点顶板最大拉应力为41.3MPa,应力分布规律符合连续梁受力特性,见图18。

图18 汽车活载(顶板)应力图(单位:MPa)
⑧汽车活载下的应力结果(底板)
汽车活载作用下的主梁标准组合中支点底板最大压应力为108.5MPa,应力分布规律符合连续梁受力特性,见图19。

图19 汽车活载(底板)应力图(单位:MPa)
3.2.3U肋单梁模型
模型共计采用41 个节点、40 个单元。单元截面为U-2 型闭口加劲肋,顶宽300mm、底宽170mm、高280mm、厚8mm 以及布置间距550mm 的主梁顶板。截面有效宽度考虑剪力滞效应及局部受压稳定的折减。板肋与横隔板连接处采用全固结支座模拟,汽车荷载采用车辆荷载(城A)。考虑到模型结构的截面宽度为550mm,根据规范,单个车轮的宽度为600mm,因此该模型的汽车荷载横向分布系数采用0.5×550/600=0.458,冲击系数按局部加载取0.4,见图20、图21。

图20 结构离散模型

图21 单元截面(单位:mm)
①自重恒载下的反力结果
自重恒载作用下的主梁支座竖向反力合计为45952.5N,即梁的自重为4.7t,显示单梁模型的外部边界条件模拟较为可靠,见图22。

图22 自重恒载反力图(单位:N)
②自重恒载下的内力(纵向弯矩My)结果
自重恒载作用下的主梁标准组合内力(弯矩)结果显示主梁跨中处正弯矩最大为191468.6N·mm,中支点处负弯矩最大为382973.1N·mm,内力分布规律符合连续梁受力特性,见图23。

图23 自重恒载内力图(单位:N·mm)
③自重恒载下的应力结果(顶板)
自重恒载作用下的主梁标准组合支点顶板最大拉应力为0.3MPa,应力分布规律符合连续梁受力特性,见图24。

图24 自重恒载(顶板)应力图(单位:MPa)
④自重恒载下的应力结果(底板)
自重恒载作用下的主梁标准组合支点底板最大压应力为0.7MPa,应力分布规律符合连续梁受力特性,见图25。

图25 自重恒载(底板)应力图(单位:MPa)
⑤汽车活载下的反力结果
汽车活载作用下的主梁支座竖向反力结果显示单梁模型的外部边界条件模拟较为可靠,见图26。

图26 汽车活载反力图(单位:N)
⑥汽车活载下的内力(纵向弯矩My)结果
汽车活载作用下的主梁标准组合内力(弯矩)结果显示主梁跨中处正弯矩最大为36.9kN·m,中支点处最大负弯矩为30.5kN·m,内力分布规律符合连续梁受力特性,见图27。

图27 汽车活载内力图(单位:N·mm)
⑦汽车活载下的应力结果(顶板)
汽车活载作用下的主梁标准组合支点顶板最大拉应力为22.6MPa,应力分布规律符合连续梁受力特性,见图28。

图28 汽车活载(顶板)应力图(单位:MPa)
⑧汽车活载下的应力结果(底板)
汽车活载作用下的主梁标准组合中支点底板最大压应力为53.0MPa,应力分布规律符合连续梁受力特性,见图29。

图29 汽车活载(底板)应力图(单位:MPa)
3.2.4 板壳模型
模型共计采用8525 个节点、6423个单元。单元均为薄板单元,厚度采用相应的实际设计值,模型包含主要构件的顶、底、腹板及其纵向加劲肋,以及翼缘板横隔板、实腹式横板和框架横隔板。
为方便核查结果,活载仅设置车道荷载,采用城-A 级,两车道左偏布载,见图30、图31。

图30 车道布载示意
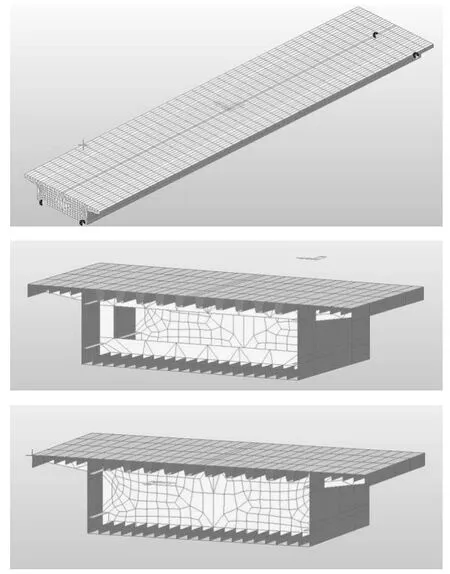
图31 结构离散模型
①自重恒载下的反力结果
自重恒载作用下的主梁每个支座竖向反力均为443127.0N,即梁的自重为1772508.0N(180.7t),显示板壳模型的外部边界条件模拟较为可靠,与单梁单元计算结果基本一致,见图32。

图32 自重恒载反力图(单位:N)
②自重恒载下的应力结果(顶板)
自重恒载作用下的主梁标准组合顶板最大压应力为21.9MPa,应力分布规律符合简支梁受力特性,见图33。

图33 自重恒载(顶板)应力图(单位:MPa)
③自重恒载下的应力结果(顶板板肋)
自重恒载作用下的主梁标准组合顶板板肋最大压应力为21.6MPa,应力分布规律符合简支梁受力特性,见图34。

图34 自重恒载板肋应力图(单位:MPa)
④自重恒载下的应力结果(顶板U肋)
自重恒载作用下的主梁标准组合顶板U 肋最大压应力为21.9MPa,应力分布规律符合简支梁受力特性,见图35。

图35 自重恒载U肋应力图(单位:MPa)
⑤汽车活载下的反力结果
汽车活载作用下的主梁偏载一侧的两个支座竖向反力为1064765.8N,另一侧两个支座竖向反力为541449.0N,显示板壳模型的外部边界条件模拟较为可靠,与单梁单元计算结果基本一致,见图36。
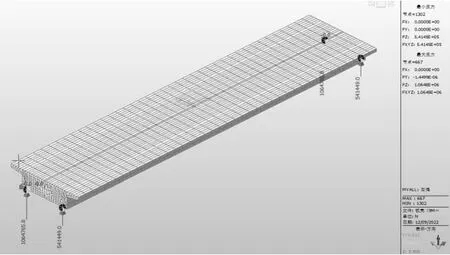
图36 汽车活载反力图(单位:N)
⑥汽车活载下的应力结果(顶板)
汽车活载作用下的主梁标准组合顶板最大压应力为65.3MPa,应力分布规律符合简支梁受力特性,见图37。

图37 汽车活载顶板应力图(单位:N·mm)
⑦汽车活载下的应力结果(顶板板肋)
汽车活载作用下的主梁标准组合顶板最大压应力为113.8MPa,应力分布规律符合简支梁受力特性,见图38。

图38 汽车活载板肋应力图(单位:MPa)
⑧汽车活载下的应力结果(顶板U肋)
汽车活载作用下的主梁标准组合顶板最大压应力为86.4MPa,应力分布规律符合简支梁受力特性,见图39。

图39 汽车活载U肋应力图(单位:MPa)
3.3 结果假设与对比验证
3.3.1 仅考虑主梁单梁模型第一体系结果与板壳单元模型结果的对比
由表1 可知,两个模型的结果中恒载作用基本相同,而活载作用(汽车)的应力结果差别较大(113.8-33.5=80.3 MPa),差值接近2.4 倍,而基本组合下结果的差别也较大(185.6-73.2=112.4 MPa),差值超过1.5 倍。显然,对于承受直接荷载作用于桥面顶板的主梁,仅考虑第一体系的结果是不合理的。

表1 最不利应力σmax结果表(单位:MPa)
因此,如何考虑第一与第二体系两个结果,并结合目前国内现行规范进行设计验算,最直接的方式就是第一体系结果+第二体系结果,再与欧洲及日本规范的规定进行对比,选择较为可靠的设计验算方法。
3.3.2 主梁单梁模型第一体系结果及第二体系纵向加劲肋结果的线性叠加
由表2 可知,直接将单梁第一体系的顶板结果与第二体系纵向加劲肋结果进行线性叠加后,其与板壳模型的结果接近,但仍有一定的差距,其中活载差值约25%,基本组合差值约22%,虽然直接线性叠加的结果对结构设计是偏安全保守的,但这种差距在设计时是不可接受的。
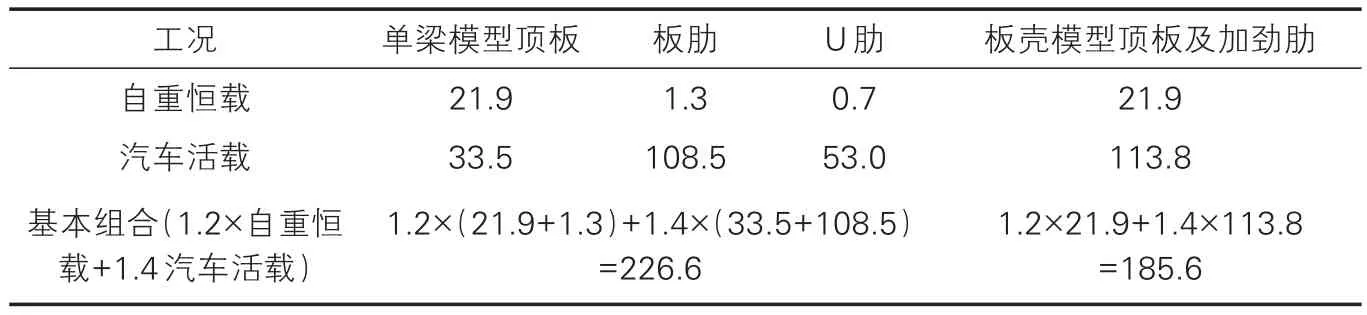
表2 最不利应力σmax结果表(单位:MPa)
3.3.3 按欧洲规范叠加结果
由表3 可知,根据欧洲规范考虑两种体系活载应力结果叠加后进行验算,活载应力结果与板壳模型结果接近,差值约16%,基本组合差值约15%,其结果对结构设计仍是偏于安全保守的,且相较于两种体系的直接叠加,差值较小。
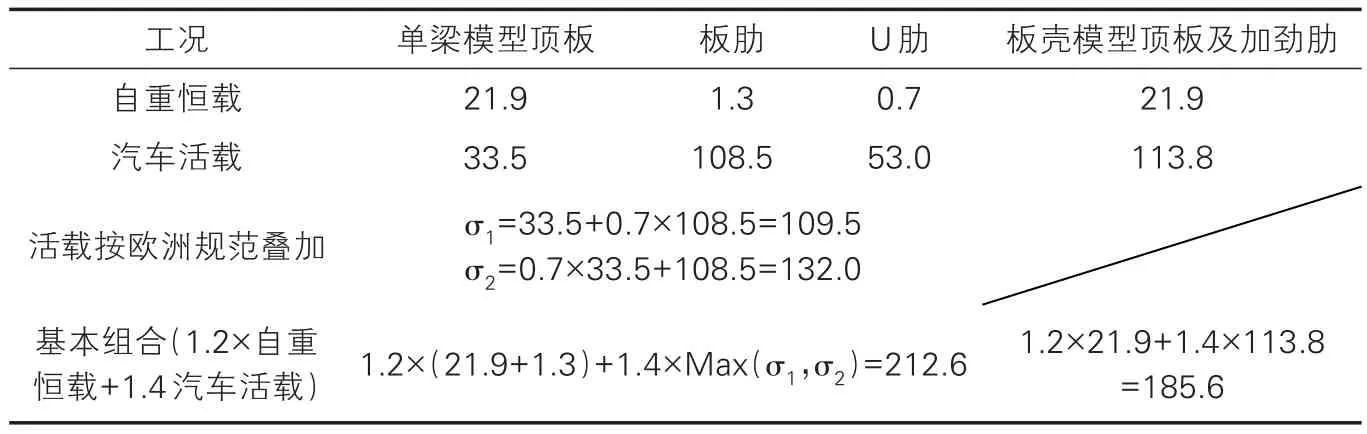
表3 最不利应力σmax结果表(单位:MPa)
3.3.4 按日本规范叠加结果
此方式的两种体系叠加计算结果即为其直接叠加的基本组合结果,根据表3,其结果为226.6MPa。
按《公路钢结构桥梁设计规范》(JTG D64-2015),其验算结果为226.6MPa≤fd=270MPa,结构安全富余约16%;板壳单元的基本组合结果验算为185.6MPa≤fd=270MPa,结构安全富余约31%。
而按日本相关设计规范,其验算结果 为 226.6MPa≤1.4×fd=1.4×270=378MPa,其结构安全富余约40%。
由上述对比可见,根据日本规范考虑两种体系活载应力结果的叠加后的验算,其结构安全的富余度较板壳单元模型结果偏不保守。考虑到本次计算模型仅考虑了结构自重的恒载作用及两车道的汽车活载作用参与验算组合,当计算模型的作用荷载增加,例如二期恒载作用、温度及风荷载作用等,使桥面板的汽车荷载作用效应进一步占比减小,其将验算允许限值增加1.4 倍的设计方式对结构而言偏不安全。
4 结束语
目前国内对正交异性钢桥面板结构的两种传力体系如何叠加验算没有明确规定,如何考虑其验算方式对结构的设计合理性起着至关重要的影响。
根据本次建模计算结果的研究对比可知,采用日本规范的验算规定,其整体结果偏于不安全;而采用欧洲规范的验算规定,整体结果偏于安全,且相较于两种体系的直接线形叠加的验算方式,与板壳单元的验算结果差值更为接近,是一种较为可靠的验算方式,可以为广大设计单位在进行相关结构设计计算时提供有效的参考。
