圬工拱桥UHPC加固方案分析
2024-05-15崔德军
崔德军
(重庆市市政设施运行保障中心,重庆 400015)
随着交通运输基础建设事业的飞速发展,桥梁的数量日益增多,规模也越来越大,根据交通运输部2021年数据统计:全国公路桥梁96.11万座,比上年末分别增加4.84万座,其中特大桥梁7 417座,大桥13.45万座。总的来说,桥梁基数的增加,随之而来的是桥梁服役的年限逐年增加。从大量实例中可以看出,多数桥梁一般在投入使用运营30年后,就会面临桥梁正常使用功能下降的问题,结构构件及材料出现耐久性问题甚至面临安全性问题。目前我国公路服役中的桥梁约40%桥龄超过20年,技术状况等级为三、四类的桥梁约占30%,超过10万座桥梁成为危桥,相比美国42%的桥梁至少有50年的历史,安全隐患不容忽视。
在各种桥型中,圬工拱桥历史最为悠久,是我国早期经常使用的桥梁结构形式,在服役桥梁中占有较大的比重。但由于建设年代早、荷载设计标准偏低,随着交通量的逐步增加,圬工拱桥出现了大量的病害,亟待开展针对性的病害治理与结构性能提升工作。这其中拱圈裂缝是最常见的病害之一,是桥梁结构实际状况的直观表现[1-2]。因此,加强对拱圈开裂的研究,阐明裂纹产生的机理,对于桥梁的修复和性能提升具有理论和实际意义。在实际工程的基础上,阐述了圬工拱桥拱圈设计的基本理论,并结合断裂力学原理,分析拱圈裂缝产生的原因,进而提出利用超高性能混凝土(Ultra-high Performance Concrete,UHPC)进行加固的方案。
1 圬工拱圈设计计算理论
对于拱桥而言,随着裂缝的不断发展,截面弯矩不断减小,而轴力却相对增大。因此截面的开裂深度与内力大小并不是线性关系[3]。在国内外,大量学者都对混凝土拱桥裂缝建立了有限元模型并进行了相关的力学分析,但是对圬工拱结构开裂状态下的结构力学性能尚没有进行深入的分析。
1.1 无铰拱理论
根据拱的约束条件,一般可将它视为无铰拱,因此可用弹性中心法求得各截面内力。力学方程为
δ11X1+ΔP1p=0δ22X2+ΔP2p=0δ3X3+ΔP3p=0
(1)
式中:X1、X2、X3分别为单位轴力、单位剪力和单位弯矩;δ11、δ2、δ33分别为X1、X2、X3方向发生的位移;ΔP1p、ΔP2p、ΔP3p分别为荷载P作用下X1、X2、X3方向发生的位移。
由图1、图2,根据结构的平衡条件,可得
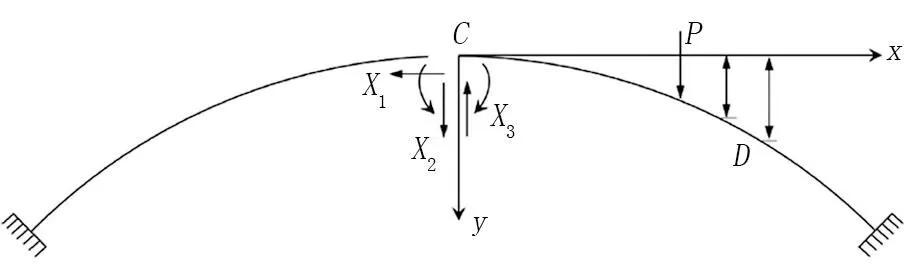
图1 固结模式拱内力计算简化模型
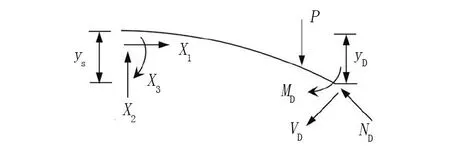
图2 固结模式拱内力计算隔离体
MD=X1(yD-ys)+X2xD+X3+Mp
VD=X1sinφD+X2cosφD+Vp
ND=X1cosφD-X2sinφD+Np
(2)
式中:ND、VD、MD分别为截面D处的轴力、剪力、弯矩反力;Np、Vp、Mp分别为荷载P在截面D处产生的轴力、剪力、弯矩反力;yD、ys分别为截面D、C的竖向坐标;xD为截面D的横向坐标;φD为截面D的法线与x坐标的夹角。
1.2 平铰拱理论
当石拱桥拱脚开裂时,将其视为铰接或者固接都会有较大的误差,因为其既能承受轴力,又能承受弯矩,并且能通过微小的转动释放一部分弯矩,因此通常可以将其视为平铰,这种理论也经常用于分析拱身开裂的石拱桥。
2 圬工拱圈开裂原因分析
因石砌拱圈采用分环砌筑,环与环之间搭接不良容易产生纵向裂缝;拱上侧墙土压力的拉扯作用使拱圈产生裂缝;结构本身的特殊受力原因,弯扭组合使本身承受拉应力很弱的石拱承受过大的拉应力,使拱圈被拉坏产生裂缝;拱上侧墙和桥台侧墙连在一起,在较大的侧土压力的共同作用下,桥台不可避免地将发生侧向受力变形。
但是,传统的圬工拱圈纵向开裂原因只能适用于部分地区中的小范围圬工拱圈。在对重庆等西南片区的石拱桥的定期检查中可以了解到,上述开裂的原因都不能很好地解释大多数拱圈的开裂。但是,这些石拱桥开裂的共通点为:如果渗水发生在条石之间的砂浆砌缝,大多数条石在砌缝的方向上都会产生裂缝。综合考虑桥梁的正常工作使用寿命、环境等各种因素的不同,出现的纵向裂缝的长度和宽度也不同。因此,裂缝的扩展与伸长才是圬工拱圈纵向开裂的主要原因。
3 基于断裂力学的拱圈裂缝拓展理论
条石的堆砌组合构造了现有的石拱桥的拱圈,水泥砂浆填充在条石与条石之间,那必然在条石界面之间存在凹凸不平,这些凸起会产生空隙,加上水泥砂浆强度差易受到温度变形的影响,因此极易形成早期裂缝。
在西南片区特别是重庆区域内,运营时间超过10年的石拱桥非常常见,自然环境较为险恶,空气中湿度较大,并持续受到外荷载的影响,拱圈灰缝中的裂缝极易发展直至贯通整个截面,甚至导致灰缝脱落并出现渗水、泛碱现象。
通过断裂力学理论可知,应力的奇异性是由拱圈的裂纹所导致的,即应力集中现象将在裂纹尖端有着强烈的展现。伴随着裂纹的发生,结构的强度将显著降低。裂纹的发展将被应力强度因子所掌控,裂纹在应力强度因子达到其临界值时,将扩展直至拱圈破坏[4]。
拱桥是一种以承压为主的结构,然而从竖向看,两排条石之间的联系其实较为薄弱,可以认为板拱中存在纵向裂缝。
拱圈条石按受力情况可以划分为双向均匀受压板、单向均匀受拉板和四周均匀受剪板等三种情况,见图3。
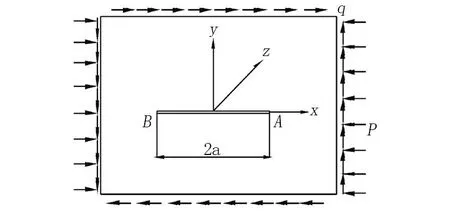
图3 拱圈纵向裂缝与条石脱离的受力情况
设p=σ,q=τ,双向均匀受压板和单向均匀受拉板在裂纹尖端场叠加后的应力分量表达式为
δx=σ
δy=0
τxy=0
(3)
式中:δx为x方向的应力;δy为y方向的应力;τxy为剪应力。
分解图4中(c)为Ⅱ型加载下经典裂纹问题,Westergaard应力函数为
(4)
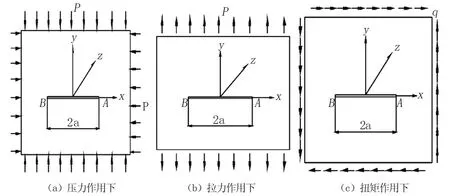
图4 纵向裂缝受力分解图
式中:ZII(z)为复变解析函数;a为裂纹的半长;z为纵坐标。
Westergaard应力函数的应力分量和位移分量表达式为
(5)
式中:y为竖坐标;B为常数,可取为τ;Re(·)为复数的实部;Im(·)为复数的虚部。
以及
(6)
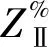
将公式(4)代入公式(5)和(6),可以求得裂纹尖端区域(r< (7) 以及 (8) 可知,当r< (1)整体性较好。裂缝形成后会迅速发展,甚至贯穿整个主拱圈。 (2)整体性较差。当裂缝进入条石间的横向连接缝时,会横向发展。 根据断裂力学理论,裂缝的尖端往往会应力集中,集中的区域汇集了大量能量。而能量释放时一般向着结构最薄弱的地方进行。因此,裂缝一旦形成,由于能量的释放,其会不断发展扩大,最终导致石拱桥承载能力降低,甚至危及桥梁安全。 红岩桥位于黔南州长顺县云盘至鼓扬的农村公路上,桥梁中心桩号为K18+907,该桥于1984年12月12日建成通车。桥梁全长25.0 m,跨径组合为1×4.2 m+1×5.1 m+1×4.2 m。桥面总宽5.0 m,净宽4.4 m。桥梁设计荷载为汽车—15级,跨越摆所河。 根据现场勘查以及定期检查报告,该桥总体技术状况等级为4类,主要存在以下表观病害。 (1)主拱圈:主拱圈为石砌拱,渗水、碱蚀多处;主拱圈底部勾缝砂浆脱落严重;主拱圈裂缝3条,总长度为3.2 m;拱圈轻微下挠,砌块脱落1处,面积为250 cm2。 (2)下部结构:本桥为浆砌块石重力式桥墩。经检查,桥墩砌石水蚀、风化。 (3)桥面铺装:原桥为沥青混凝土桥面铺装,破损非常严重,总面积为23.1 m2,但经实际勘察发现该病害经过处治,现为水泥混凝土路面。 根据该桥的病害情况,结合普通混凝土加固圬工拱桥的经验,确定主拱圈采用UHPC加固,桥墩采用普通C40混凝土加固,加固厚度均为15 cm。加固层中配置一层受力钢筋网,纵向钢筋直径为20 mm,横向钢筋直径为12 mm,间距均取20 cm。加固层同原结构采用锚杆的方式粘结,锚杆直径12 mm,分别植入原拱圈和桥墩深度20 cm、15 cm,空间上呈梅花形布置。UHPC的组分和制备方法应该符合现行国家标准《活性粉末混凝土》(GB/T 31387—2015)的相应要求,抗拉强度满足UHPC-1的材料性能要求(7 d抗拉强度为6.21 MPa)。在此基础上,建立了桥梁的有限元模型,并开展了桥梁承载能力的验算。 承载能力极限状态下,根据《公路圬工桥涵设计规范》(JTG D61—2005),圬工拱桥结构承载力检算应符合下式要求。 当e≤0.6S时 γ0Nd≤αyφAZiξefcd (9) 当e>0.6S时 (10) 式中各参数见规范规定。 (1)承载力检算系数。 按下式计算确定结构承载能力检算系数评定标度d。 d=∑αjdj (11) 式中:αj为某项检测指标权重值,按表1取值;dj为结构某项检测指标的评定标度。 表1 承载能力检算系数检测指标权重值 分别计算主桥上部主要承重构件与桥墩结构承载能力检算系数评定标度d,见表2。 表2 结构承载能力检算系数评定标度d计算结果 根据结构承载能力检算系数评定标度,依据表3确定桥梁承载能力检算系数Z1值。 表3 配筋混凝土桥梁的承载能力检算系数Z1值 由表3知,本桥主桥部分检算系数Z1取值为0.96。 (2)混凝土截面及圬工拱桥折减系数。 配筋桥梁结构或构件的截面折减系数ξC,应根据截面损伤的综合评定标度按表4确定。 表4 截面折减系数值 表5 材料风化、碳化及物理与化学损伤权重 其中,R=∑αjRj,主桥上部承重构件与桥墩评定如下。 综上评定,确定主桥上部承重构件与桥墩的界面折减系数ξC=0.93。 (3)计算结果。 因本桥上部结构对称,对主拱圈进行验算。表6~表8列出了该桥在恒载及公路—Ⅱ级活载组合作用下主拱圈加固前控制截面(拱脚、1/4截面、1/2截面)的内力分析验算结果。 表6 1#拱圈加固后承载能力检算部分结果 表7 2#拱圈加固后承载能力检算部分结果 表8 3#拱圈加固后承载能力检算部分结果 由表6~表8可知,采用UHPC加固后,圬工拱桥的承载能力有很大的提升,全桥整体应力水平显著下降,各关键截面的验算结果均合格,表明所提加固方案能使桥梁满足正常使用极限和承载能力极限状态要求。 (1)腹拱圈设计计算目前主要有三种模式,即无铰拱理论、铰接理论和平铰拱理论,由于运营中的石拱桥拱脚处开裂现象普遍,因此,介于无铰拱与铰接之间的平铰理论运用最多。 (2)基于断裂力学理论,分析了拱桥纵向开裂的成因。圬工砌体抗拉强度远小于抗压强度,在结构出现一定拉应力时便会产生裂缝,而裂缝的尖端会汇聚大量的能量,并朝着结构薄弱的地方发展,导致裂缝的拓展,进而损害石拱桥的承载能力,甚至危害桥梁结构的安全。 (3)采用UHPC加固后,圬工拱桥的承载能力有很大的提升,采用UHPC材料进行套箍加固后,全桥整体应力水平显著下降。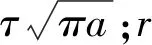
4 UHPC加固拱桥实例分析
4.1 工程概况
4.2 分析计算方法



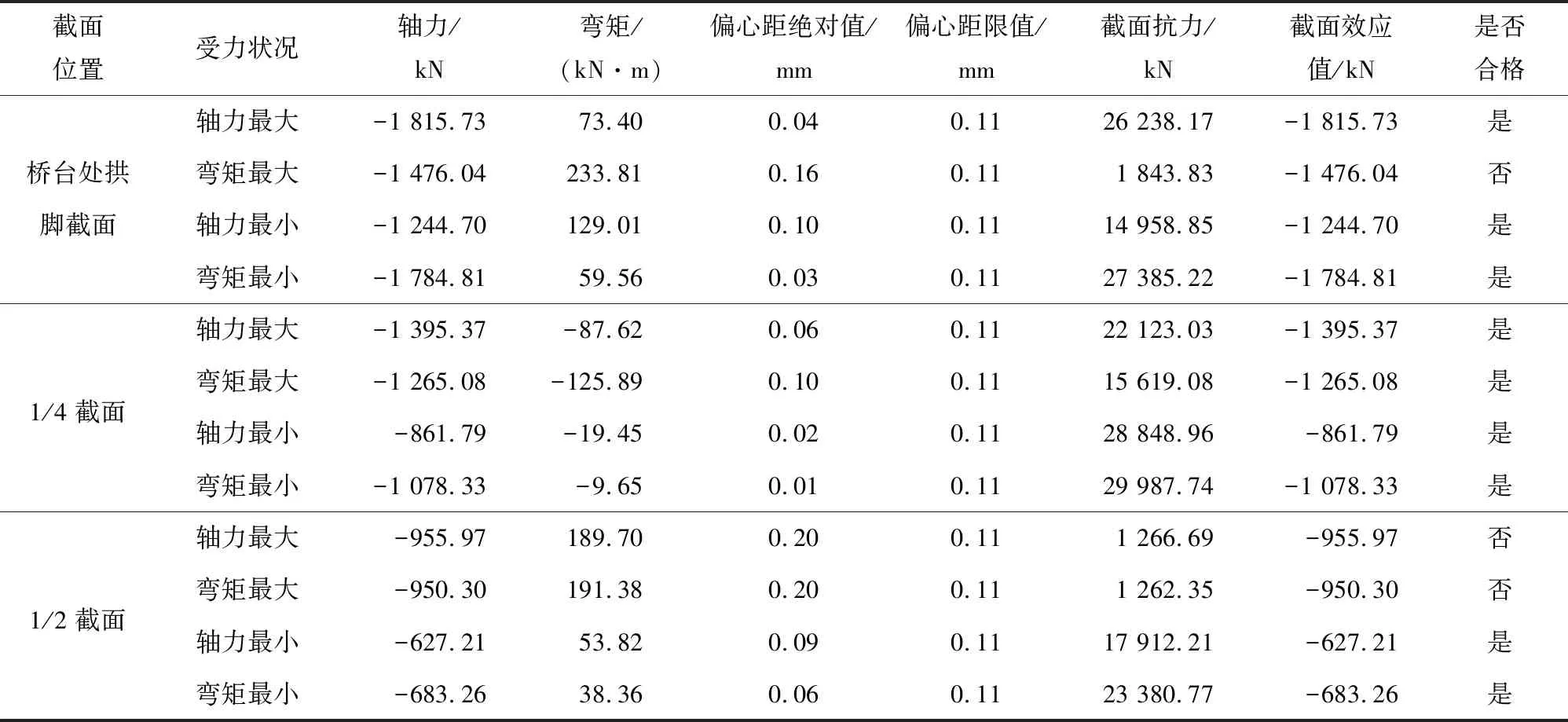
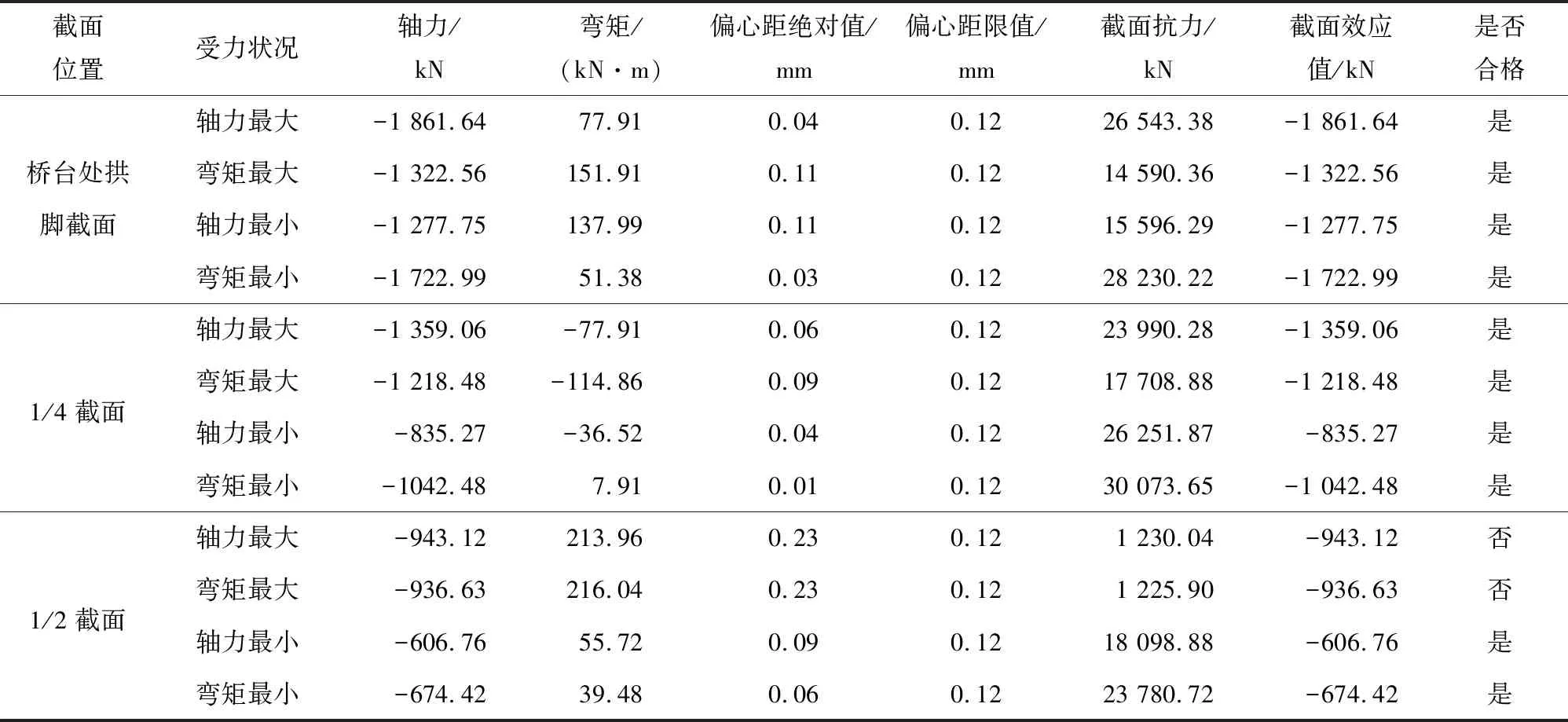
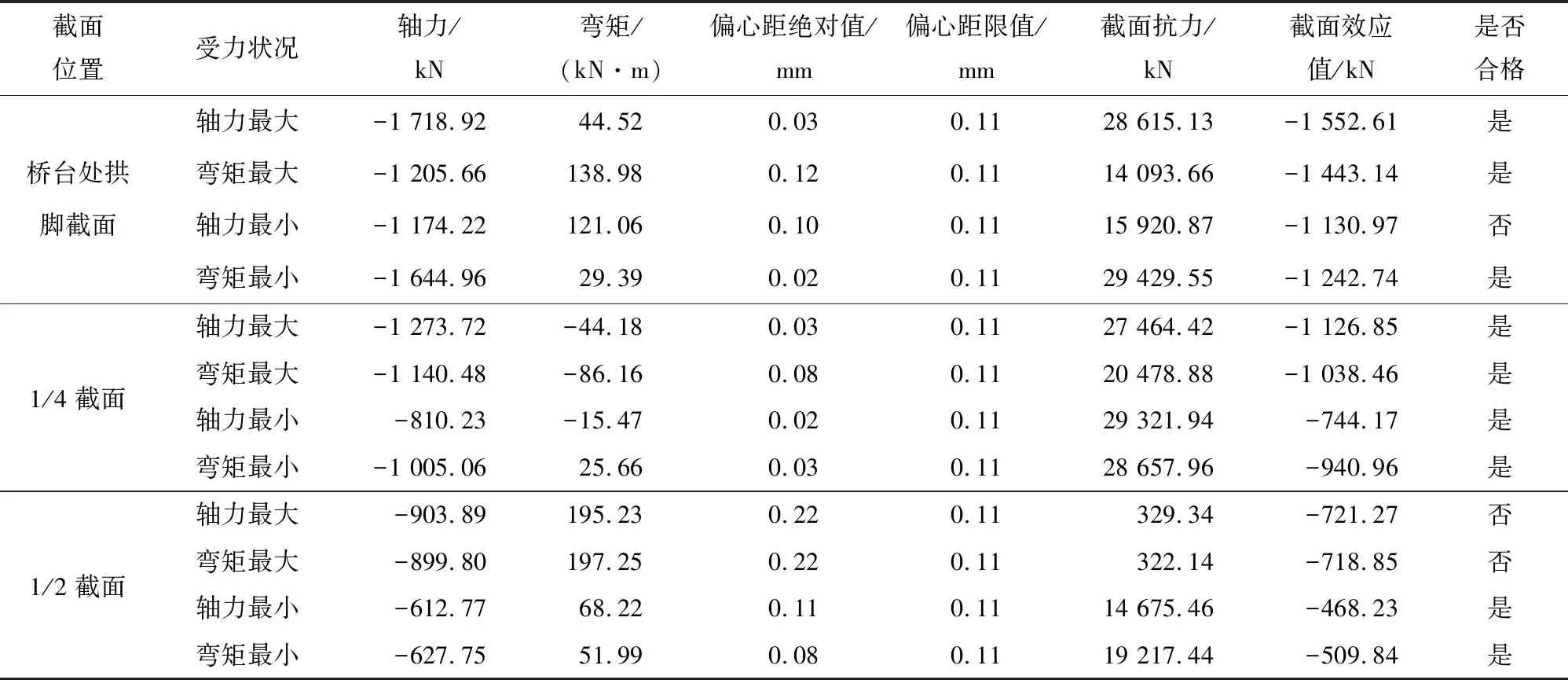
5 结 论
