异形钢拱塔桥梁温度效应分析

陈立忠

(中国水利水电第一工程局有限公司,吉林 长春 130033)

钢箱梁具有自重轻、强度高、施工便捷等特点,因此近年来在城市桥梁施工中得到了广泛运用。由于钢材导热性能好,温度作用对钢结构的影响显著[1]。虽然目前对钢箱梁温度效应的研究取得了一些成果,但影响温度场的因素众多(如日照和风力等),不可能全面考虑所有影响因素。另外,虽然我国规范对钢桥的温度作用做了相关规定,但我国幅员辽阔、各地温度差异性较大,规范中的温度作用模式与实际温度场之间的区别还有待进一步研究。有研究者开展了温度场实测试验,但研究成果大多仅适用于桥址处附近的地区[2-3]。此外,随着对桥梁美观度要求的提高,异形斜拉桥的数量日益增多,但异形桥梁结构受力复杂,温度效应的影响也更加突出[4-5],因此有必要对异形斜拉桥的温度效应开展相应的研究。

张玉平等[6]根据传热学和有限元原理,基于实测数据,运用线性函数和指数函数拟合了无铺装层钢箱梁日照条件下的温度梯度。李传习等[7]结合杭州江东大桥的施工监控对钢箱梁的日照温差分布进行观测分析。聂玉东等[8]对气候环境比较恶劣、天气非常寒冷地区的混凝土梁桥做相应的温控和检测,对大量的实测数据进行统计和分析,发现桥梁箱型梁的温差主要集中在箱梁腹板的内部,顶、底板的温差反而较小。以大庆市秀水路跨线桥为工程背景,以4个国家的规范中温度梯度模式的规定为基础,研究了异形钢拱塔斜拉桥在不同温度梯度模式和系统温度变化下的温度应力。

1 工程概况

大庆市秀水路跨线桥为单索面异型拱塔斜拉桥,桥塔造型为拱塔形式,与水平面夹角为65°,全长96.3 m(含钢混结合段),拱塔最高为26.344 m(基于塔座顶)。拱塔塔底设置塔座,钢塔根部锚入塔靴4 m。钢塔均为单箱单室倒梯形钢结构,倒梯形顶部宽3～4.3 m,底板宽0.8 m,沿拱塔轴向为变截面,顶底板厚30 mm,腹板厚30 mm,顶底板、腹板纵向采用I型加劲肋。钢塔分节段在工厂预制。各节段在工厂预制并进行预拼装,完成后运至现场,采用由根部向塔顶吊装,节段吊装就位后采用对接熔透焊方式形成整体。

主梁采用三跨连续钢箱梁,单箱双室斜腹板断面,钢梁宽度为6.2 m,梁高1.5 m,钢箱梁顶底板设置单向1.0%横坡,在边跨渐变到平坡;钢箱梁顶板、腹板厚为12 mm,底板厚为16 mm。纵向采用I型加劲肋,加劲板高120 mm,厚12 mm。横隔板采用实腹式横隔板,标准段布置间距为2 m,横隔板厚度为12 mm;支点处横隔板厚度加强至16 mm。桥梁全长94 m,分节段在工厂预制。各节段在工厂预制完成后运至现场,采用由支点向跨中吊装,节段吊装就位后采用对接熔透焊方式形成整体。桥面铺装采用3 cm彩色混凝土沥青。支座采用板式橡胶支座。

斜拉索顺桥向间距4 m,全桥共计13根斜拉索,对称布置。斜拉索索体采用镀锌铝合金钢丝双层HDPE的防腐索体,斜拉索公称直径为37.082 mm,每根斜拉索由55股钢丝组成,钢丝强度等级1 760 MPa。桥塔塔座、承台及桩基采用混凝土结构,桩基采用钻孔灌注桩。主梁中墩采用Y形钢墩与主梁固结。Y墩上部为1.4 m×1.2 m矩形截面,壁厚30 mm,Y墩下部为2 m×1.2 m矩形截面,壁厚30 mm。连接墩桥墩采用圆形变截面钢墩,截面尺寸为0.3～0.6 m,壁厚20 mm。

2 建立有限元模型

采用midas Civil软件建立该桥的有限元模型,如图1所示。主梁、拱塔、桥墩和基础均采用梁单元模拟,斜拉索采用桁架单元模拟。斜拉索底端与主梁采用弹性连接(刚性)连接。承台底部采用节点弹性支撑模拟桩基提供的平动和转动刚度。桥梁地震反应分析中,桩基础的常用处理方法是在承台底加六个方向的弹簧来模拟桩基础的作用,如图2所示,并由承台底部内力按静力方法反推单桩最不利受力。弹簧刚度根据土层状况和桩的布置形式按静力等效原则确定,由土性资料确定m值,这种处理方法在低桩承台桩基础中广泛采用。经计算,群桩基础的六弹簧刚度如表1所示。过渡墩的板式橡胶支座采用弹性连接模拟,并按照支座的剪切刚度设置水平向刚度,板式橡胶支座的计算如公式(1)所示。

(1)

表1 群桩基础的六弹簧刚度

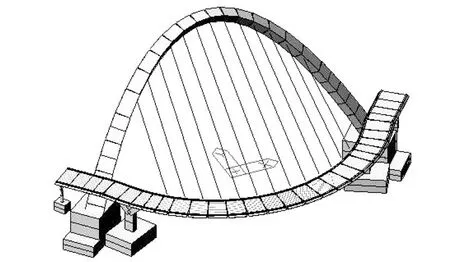
图1 秀水路跨线桥结构有限元模型

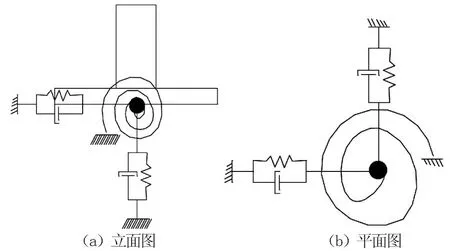
图2 桩基础的六弹簧模型

式中:k为橡胶支座的水平刚度,kN/m;Gd为橡胶支座的动剪切模量,kN/m2,一般取1 200 kN/m2;Ad为支座的剪切面积,m2;∑t为橡胶层总厚度,m。

3 各国规范温度梯度比较

3.1 英国BS-5400规范

英国BS-5400规范是各国规范中对于温度梯度规定最为详细的一本规范,在设计一些特殊桥梁,若无实测的温度场数据时,设计单位通常都会参考英国BS-5400规范[9]。英国BS-5400规范根据桥梁结构类型(混凝土桥或钢桥)以及铺装层的种类和厚度,将桥梁结构分成四种类型,并规定了相应类型桥梁的正温度梯度和负温度梯度。英国BS-5400规范的温度分布模式如图3所示。正温差为四段折线,从梁顶计算,分布间距分别为0.1 m、0.2 m和0.3 m。负温差模式只包含一段折线,从梁顶计算温度变化范围为0.5 m。

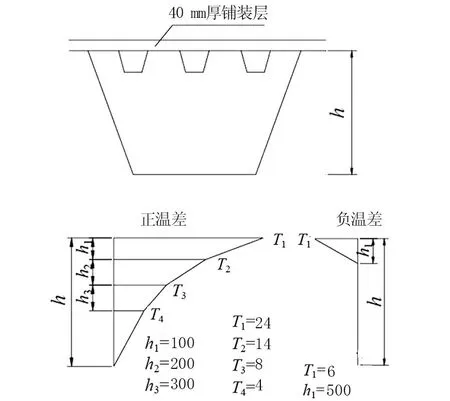
h—主梁高度,mm;h1～h3—三组从梁顶至梁底的间距,mm;T1～T4—各层顶部温度,℃。

3.2 新西兰NZBM-2003规范

新西兰NZBM-2003规范给出了钢结构和混凝土结构的温度梯度模式,该规范根据Priestley的试验和分析研究成果,采用五次幂函数描述梁体的温度梯度分布,温度梯度函数如公式(2)、公式(3)所示,温度梯度模式如图4所示。在进行分析时,可将五次幂函数采用分段的线性函数近似代替,沿梁高方向划分为4段。

(2)

h—主梁高度,mm;T1—梁顶温度,℃。

T1=32-0.2d

(3)

T1—梁顶温度,℃;T2—去除铺装层的梁顶温度,℃;T3—梁底温度,一般取0℃;A—钢梁竖向温度梯度控制参数,mm。

T1—梁顶温度,℃;T2—去除铺装层的梁顶温度,℃;A—钢梁竖向温度梯度控制参数,mm。

式中:Ty为计算点的温度,℃;T1为梁顶温度,℃;d为沥青层的厚度,mm;y为计算点到梁顶的距离,mm。

3.3 美国AASHTO规范

美国AASHTO规范温度梯度模式如图5所示,其中t为铺装层厚度,A根据梁高H确定,当H≥400 mm时,A=300 mm;当H<400 mm时,A=(H-100)mm。T1、T2根据桥梁所在地区进行取值,全美共分为4个大区,如表2所示。根据本桥例大庆市所在位置,计算时选用美国AASHTO规范的4区温度基数。负温差为正温差的-0.2倍。

表2 美国AASHTO规范温度基数取值

3.4 中国JTG D60—2015规范

中国JTG D60—2015规范参考了美国AASHTO规范的温度梯度模式,如图6所示,T1、T2选用了美国2区温度参数,但并未像ASSHTO规范一样设置不同温度分区。日照负温差为正温差的-0.5倍。

4 异形钢拱塔斜拉桥温度应力计算

4.1 正温度梯度下主梁应力

为了研究不同温度梯度模式对异形钢拱塔斜拉桥温度应力造成的差异,分别研究英国、新西兰、美国、中国规范中的温度梯度模式下的主梁应力,并将主梁应力沿主梁纵向的结果绘制如图7所示。

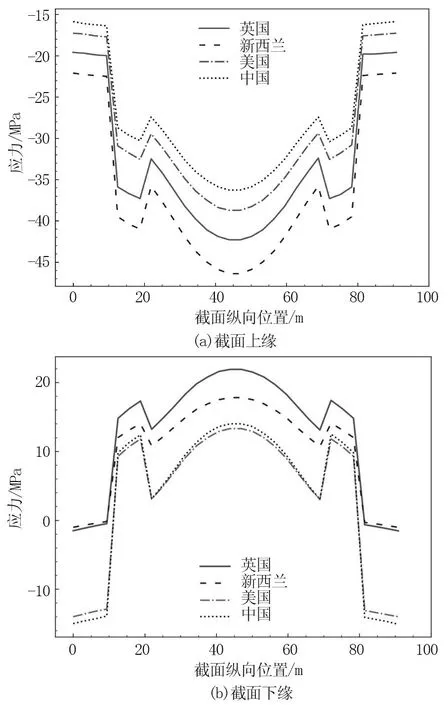
图7 4种规范正温度梯度下的主梁应力对比

根据图7(a)可以看出,不同规范下截面上缘应力纵向分布规律相似,最大应力位于主梁跨中,英国、新西兰、美国、中国规范下的最大应力分别为42.3、46.4、38.7、36.3 MPa,新西兰规范的最大应力值在4种规范当中最大,这也与文献中的研究结果一致[10],中国规范的应力值最小。主梁上缘受压应力,这是因为截面上缘温度更高,在温度作用下本应上缘伸长下缘缩短,但由于桥梁结构为超静定结构,在约束作用下主梁伸长受限,相当于外部约束为主梁施加了压力,因此上缘温度应力为压应力。除了主梁跨中应力较大外,中墩处主梁应力存在突变,应力值达到局部的极大值。由于中墩为Y形墩,主梁与中墩相交的两处位置应力均较大,而中墩分叉之间主梁温度应力大致呈平台段过渡。过渡墩由于采用的是板式橡胶支座,该处温度应力得到有效释放,温度应力较小[7]。

图7(b)为主梁截面下缘应力沿纵向的分布规律,从中可以看出,下缘应力的变化趋势与上缘应力相近,极值点分布在主梁跨中和中墩处。英国、新西兰、美国、中国规范下截面下缘的最大应力分别为21.9、17.8、13.3、14.0 MPa。英国规范的最大应力值最大,美国规范最大应力值最小。同时可发现,美国和中国规范下梁端截面下缘存在压应力,这可能是由于两者的温度梯度模式均为双折线所致,两者的截面下缘应力趋势也很接近,而英国和新西兰规范的温度模式为多段线或曲线,温度梯度沿截面变化的突变点更少。美国和中国规范下梁端截面下缘应力为负,跨中应力为正,这使得主梁的应力幅值相比英国和新西兰规范更小。

4.2 负温度梯度下主梁应力

负温度梯度下主梁应力如图8所示,图8(a)为截面上缘应力,英国、新西兰和中国规范的负温度梯度下主梁截面上缘应力相近,美国规范明显偏小,这是因为美国规范规定负温度梯度仅为正温度梯度的-0.2倍,而中国规范规定负温度梯度为正温度梯度的-0.5倍。截面上缘应力最大值位于跨中,英国、新西兰、美国、中国规范下截面上缘的最大应力分别为8.9、9.2、4.6、9.5 MPa。在中墩支点处主梁存在局部应力的极大值。图8(b)为截面下缘应力,应力最大值位于主梁跨中,中国规范的截面下缘应力最大。英国、新西兰、美国、中国规范下的截面下缘最大应力分别为2.7、5.4、4.2、8.5 MPa。

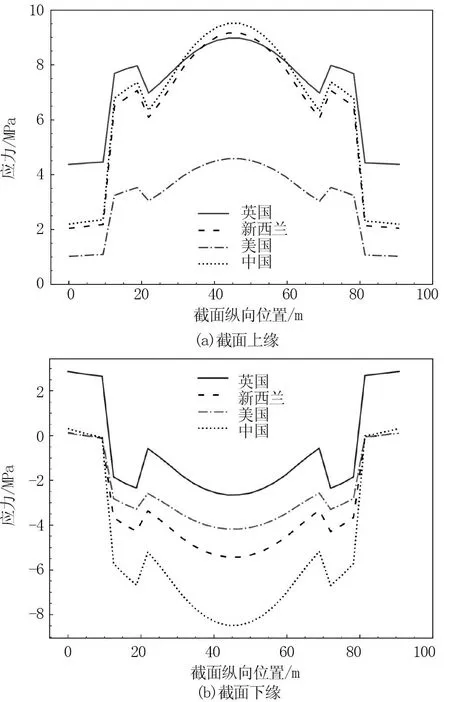
图8 4种规范负温度梯度的主梁应力对比

4.3 系统温度下主梁应力

由于异形钢拱塔桥梁为高次超静定结构,在系统温度变化下,结构也将产生温度应力。本桥例所处的大庆市全年温差显著,体系升温39 ℃,体系降温-56 ℃。系统温度变化下主梁和拱塔应力如图9所示。图9(a)为主梁应力沿桥例纵向分布,从图中可以看出,主梁的最大应力位于跨中,系统升温和系统降温下主梁最大应力分别为8.5 MPa、11.3 MPa。此外,由于中墩与主梁固结,边墩为活动支座,故主梁的应力较大区域集中在中墩到跨中区域。图9(b)为拱塔应力分布,拱塔的最大应力位于拱顶,从拱脚到拱顶应力逐渐增加。系统升温和系统降温下拱塔最大应力分别为6.1 MPa、8.8 MPa。

图9 系统温度变化下主梁和拱塔应力

5 结 论

对异型拱塔斜拉桥的温度作用开展了研究,得到以下结论。

(1)在4种规范规定的温度梯度作用模式下,异型拱塔斜拉桥主梁截面应力分布规律大致相同。其中在正温度梯度下,新西兰规范计算的截面应力最大,而中国规范计算的截面应力较小,这在一些特殊桥梁上可能是偏于不保守的。在负温度梯度作用下,美国规范下的温度梯度应力最小。

(2)在系统温度变化作用下产生的温度应力小于梯度温度作用产生的温度应力,说明该异型拱塔斜拉桥在设计分析时以考虑梯度温度作用为主。我国设计规范没有设置温度分区,可以考虑采用英国规范偏保守地进行验算。

(3)在梯度温度和系统温度下,主梁温度应力最大值均位于跨中,中墩处也存在局部应力的极大值,系统温度下拱塔的温度应力最大值位于拱顶,在进行设计时可考虑对这些部位进行加强。

(4)对异型拱塔斜拉桥温度应力的研究只考虑了竖向温度效应,而未考虑横向温度效应,主梁的上下游温度差也尚未考虑,由于这些因素,对异型拱塔斜拉桥的温度作用有待开展更深入的研究。