组合梁桥双层单元模型计算方法与验证

陈 畅,吴俊杰

(长沙理工大学土木工程学院,湖南 长沙 410114)

0 引 言

组合梁桥建模原理与其他的桥梁结构不同。在组合梁桥施工的过程中,同节段的混凝土桥面板与钢主梁并非同时安装,一般先拼装钢梁,再进行预制桥面板安装,然后浇筑湿接缝混凝土。浇筑湿接缝之前,所有因钢梁与混凝土桥面板自重产生的荷载均由钢梁承担。浇筑混凝土湿接缝后,钢主梁与桥面板互相结合,才形成整体结构共同参与受力。为了准确模拟实际工况,在建模时必须将钢梁与桥面板分开创建单元,将组合梁单元划分成双层单元。

1 双层梁单元计算原理

在双层梁单元中,上层单元模拟混凝土桥面板,赋予混凝土板的材料与截面几何特性,下层单元模拟钢主梁,赋予钢梁的材料与截面几何特性[1]。结合时,两层单元之间用刚臂进行连接。加荷载后,求解等效节点力,由公式{F}={K}×{δ}求解未知的节点位移,然后计算杆端力[2]。

1.1 带刚臂单元刚度矩阵

为局部坐标系;x′oy′为单元ab的局部坐标系;i、j为带刚臂单元节点;β为单元ab单元与轴之间的夹角;分别为刚臂ai、bj在坐标系下方向的长度;分别为刚臂ai、bj在坐标系下方向的长度。

1.2 双层梁单元刚度矩阵

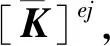
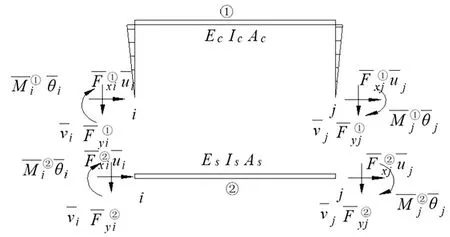
Ec、Ic、Ac、Es、Is、As分别为单元①混凝土板与单元②钢梁单元的弹性模量、截面惯性矩及截面面积;分别为混凝土板单元与钢梁单元的节点荷载矩阵;由于带刚臂混凝土板单元与普通钢梁单元存在共节点关系,故为①、②单元在i、j节点的节点位移矩阵。

1.3 初始内力、应力计算

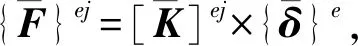
类似于一般有限元计算方法,根据钢梁单元、混凝土板单元的位移场函数式,由几何方程可以得到单元的应变场表达式,即{ε}=[B]{δ},其中[B]为单元应变矩阵。

2 工程概况

赤壁长江公路大桥为国道G351台州至小金公路跨越长江的控制性工程。主桥通航孔采用主跨为720 m的双塔对称钢-混组合梁斜拉桥,桥跨布置为90 m+240 m+720 m+240 m+90 m[5],如图3所示。主桥采用的支撑体系为半漂浮结构体系,主塔下横梁、辅助墩及边墩处均设置竖向活动支座,横向设置抗风和抗震支座[6]。主塔结构横桥向为H型结构,由塔柱及上下横梁组成[6]。主梁采用钢-混组合梁断面,桥面总宽为36.5 m,桥梁中心线处梁高3.8 m。全桥主梁横断面共有上下游两片钢主梁,每片钢主梁断面形式均为箱型,两钢主梁横桥向之间的中心距为32.52 m,设置2%的双向横坡[7]。

ZL16H、ZL17H、ZL18H为洪湖侧主梁16#节段、17#节段及18#节段编号;图中数字为单元及节点编号。

3 简支和悬臂组合梁算例分析

赤壁长江大桥主桥的主梁为双层结合梁,下层为钢主梁,上层为混凝土桥面板。在计算这种主梁时,可以直接建立双层梁模型计算。为了求证双层梁模型计算结果的准确度,以整体梁计算结果为参照,根据赤壁桥主桥标准节段的基本参数,使用上述两种不同的方法建立三节段共36 m的组合梁模型,再进行计算求解。对比两种模型的跨中挠度以及跨中截面上下缘应力,来论证两种方法计算结果是否具有一致性。

3.1 双层梁单元计算

通过自研软件建立双层梁模型:共两层单元,下层为钢主梁,上层为桥面板,单元长度均为2 m,上下两层单元之间用刚臂连接,再限制模型两端节点使其成为简支梁,双层梁模型如图3所示。其几何特性和材料特性等参数与赤壁长江大桥主梁标准节段的设计参数一致,具体取值如表1所示,荷载为双层梁的自重。

表1 截面参数表

由自研程序的输出文件可得双层梁的相关计算结果。

(1)跨中挠度:7.7 mm。

(2)跨中弯矩:钢主梁为15 835.1 kN·m,混凝土桥面板为318.7 kN·m。

(3)跨中主梁截面上下缘应力:钢主梁下缘应力为33.613 MPa,钢主梁上缘应力为-8.522 MPa;桥面板下缘应力为-0.845 MPa,桥面板上缘应力为-2.030 MPa。

3.2 整体换算单元计算

在计算整体换算单元时,设弹性模量为Ec的混凝土桥面板单元截面面积为Ac,在应力σc作用下,其应变为εc=σc/Ec。需要将其换算成等效的弹性模量为Es的钢截面,设换算后的钢截面面积为σs,应力为εs,应变为εs。等效换算后保持换算前后单元面积承受的合力大小不变和应变相等。通过换算单元法计算原理可知As=Ac/nE,nE=Es/Ec,那么上层混凝土截面便可用下层钢梁截面来代替,即可将整个截面换算为单一弹性模量Es的截面。

根据上述方法将双层梁截面换算成整体截面时,取ZL16H,ZL17H,ZL18H三节段的几何参数为计算参数,共计36 m,计钢主梁和混凝土预制板总自重均布荷载q=267.952 kN/m(此荷载与双层梁计算的自重荷载一致),以简支梁为计算模型进行计算。

3.3 计算结果对比与分析

(1)简支梁均布荷载。

计算结果对比如表2所示。

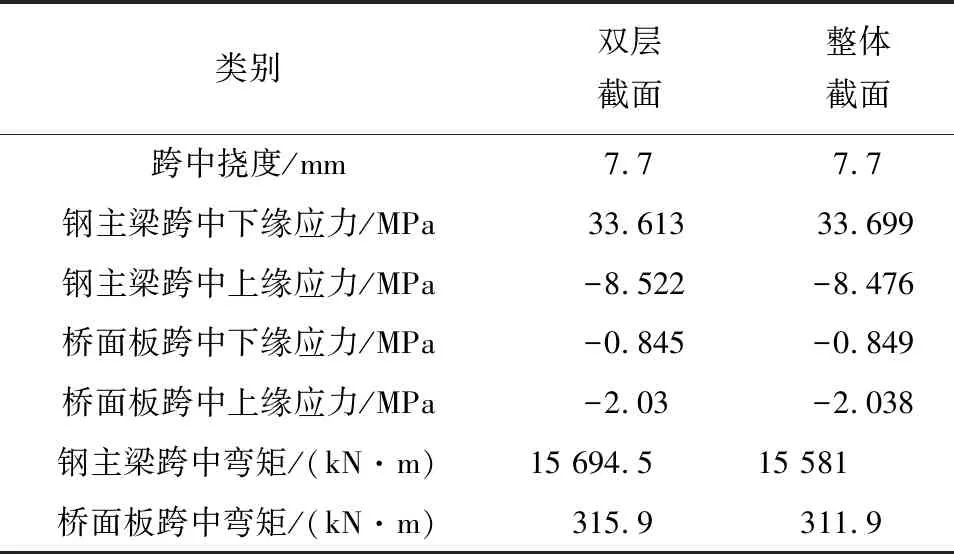
表2 均布荷载作用下计算结果的对比

由表2可知,两种计算方法的跨中挠度数值是相等的,钢主梁与混凝土桥面板跨中的上下缘应力的差值<1%,跨中弯矩的差值<1.5%。

(2)简支梁集中荷载。

将1 000 kN的集中荷载加于简支梁跨中位置,其他条件保持不变,对比结果如表3所示。

由表3可知,在保持原有计算模型不变的情况下,在跨中加1 000 kN的集中荷载后,跨中挠度的差值仍相等,钢主梁和桥面板的跨中上下缘应力有所增大,但不超过1.5%,跨中弯矩差值<3%。

(3)悬臂梁均布荷载。

上述计算采用的模型为36 m简支梁模型,根据赤壁长江大桥主梁悬臂施工的方案,现将模型改为24 m的悬臂梁模型,计算结果如表4(表中应力和弯矩的位置均为固定端)所示。

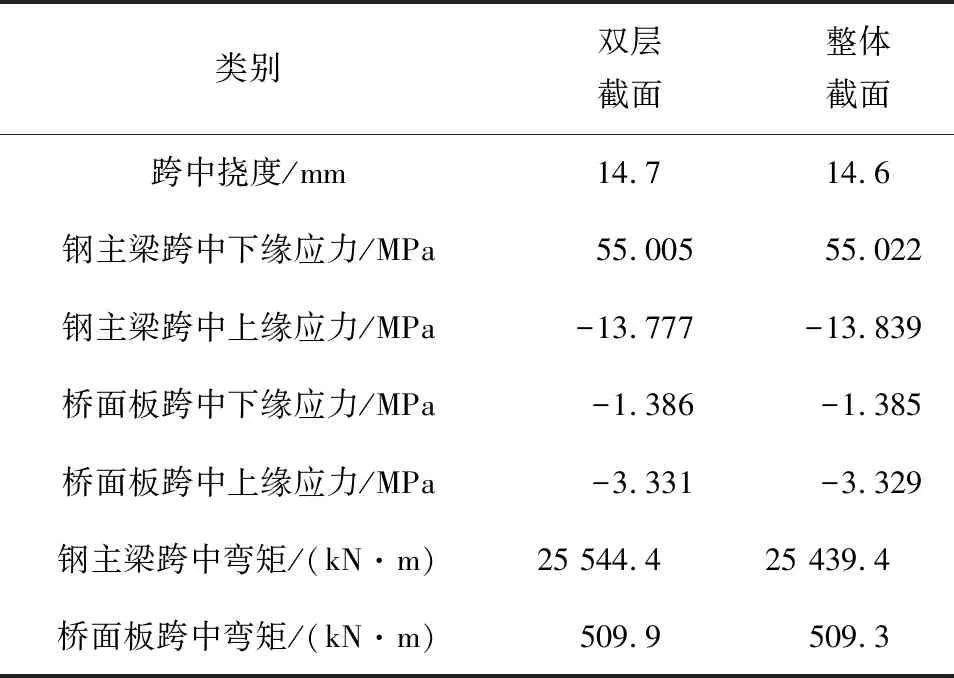
表4 悬臂状态下计算结果的对比

由表4可知,在悬臂梁模型中,两种计算结果中的悬臂端挠度差值仅相差0.1 mm,且固定端的上下缘应力以及弯矩的差值不超过1%。

上述分别对比了简支梁均布荷载、简支梁集中荷载以及悬臂梁均布荷载三种加载情况下的双层截面和换算截面的计算结果跨中各项数据的百分比差值,将表2、表3、表4的百分比差值汇总到同一张图,如图4所示。

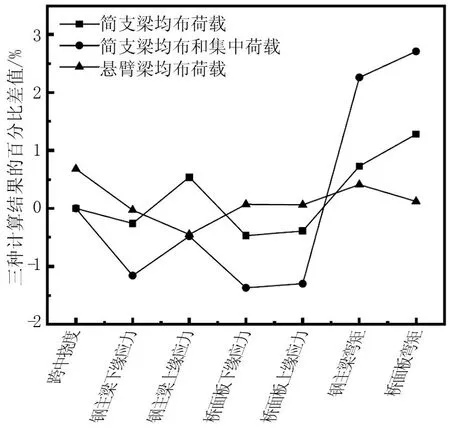
图4 三种情况计算结果的百分比差值

由图4可知,简支梁同时施加均布荷载和集中荷载模型各项数据的百分比差值相对其他两种模型的结果误差更大,但最大差值<3%。

(4)划分不同单元长度。

考虑到模型的单元长度不同可能带来计算结果的差异。上述模型中单元长度为2 m,可再将单元长度设置为1、3、6 m等三种情况进行建模计算分析,加载情况为简支梁模型施加均布荷载,1、2、3、6 m单元的双层截面与换算截面的计算结果的跨中各项数据的百分比差值如图5所示。

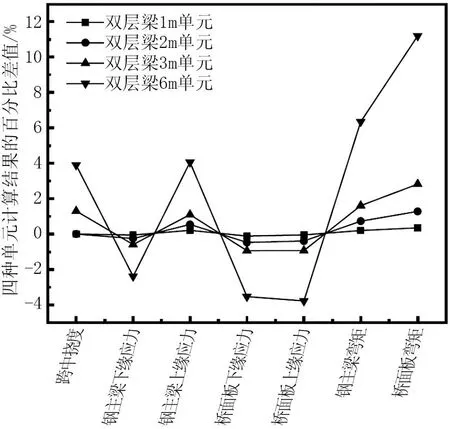
图5 不同单元长度计算结果的百分比差值

由图5可知,模型中的双层截面单元长度越小,其计算结果与换算截面值相差越小,当单元长度划分为6 m时,跨中应力差值可达4%,跨中弯矩差值可达12%。而单元长度划分为3 m时,其计算结果各项数据百分比差值都<3%。1 m和2 m单元的计算结果各项数据百分比差值都<1.5%,相较于3 m和6 m单元的计算结果更准确。

(5)考虑不同承重截面。

上述双层梁模型中的钢梁和桥面板自重荷载都加在钢梁上。现将模型里的自重荷载全部加于桥面板上,选取单元长度为2 m和3 m的模型进行计算对比分析,计算结果如下。

不同承重截面模型计算结果的跨中各项数据的百分比差值如图6所示。

图6 不同承重截面和不同单元长度计算结果的百分比差值

当模型中的荷载作用在桥面板上时,桥面板上缘应力会增大,而桥面板下缘应力等三组应力值会减小,作用在桥面板上的百分比差值最大可达20%。荷载作用在桥面板上时,钢主梁的跨中弯矩有所增大,桥面板的跨中弯矩明显减小,百分比差值达60%。

3.4 考虑徐变效应的双层梁算例分析

在上述悬臂梁模型中加入徐变计算,将自研程序中徐变计算工况时间划分为0、5、15、50、100、200、500、1 000、2 000、5 000、10 000 d,然后统计各时间点的悬臂端节点的位移值,再与根据规范计算的徐变结果进行对比验证[8-9]。

当混凝土初始龄期为180 d时,软件计算的位移与根据规范手算所得的位移对比如图7所示。

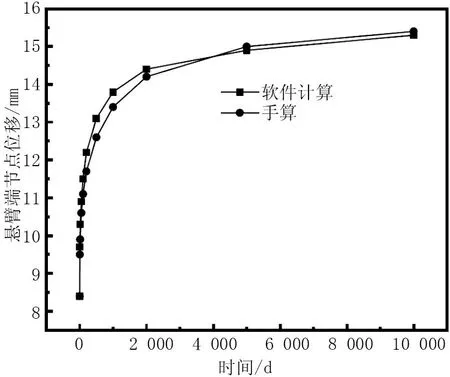
图7 初始龄期180 d时的徐变趋势对比

当混凝土初始龄期为7 d时,软件计算的位移与手算的位移对比如图8所示。

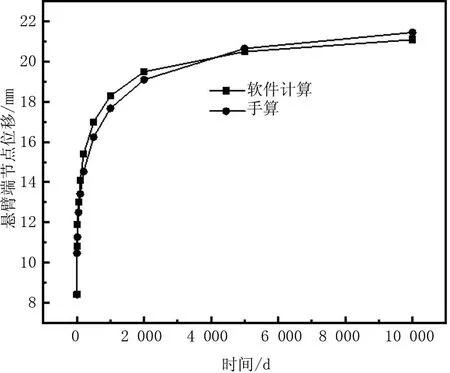
图8 初始龄期7 d时的徐变趋势对比

3.5 结果分析

(1)在计算考虑混凝土徐变时,徐变时间在1 000 d内,两种计算的挠度位移基本一致。1 000 d之后,两种计算结果存在差值,但差值百分比都在10%之内。

(2)混凝土的初始加载龄期越长,徐变对位移增量的影响越小。

总体来说,软件计算的徐变位移与规范算得的徐变位移结果较为接近。

4 结 论

(1)在不同的结构方式(简支梁或悬臂梁)和不同的荷载类型(均布荷载或集中荷载)条件下,自研程序计算出的双层梁模型计算结果与换算截面的计算结果数据基本吻合。

(2)当单元长度为2 m或2 m以内时,两种截面计算结果的百分比差值<1.5%,即在单元划分长度较小时双层梁单元模拟具有较高准确性。

(3)当模型中荷载作用在桥面板上时,计算结果差值>10%,即在建模时荷载作用位置会对模拟结果产生较大的影响,应当把荷载加在钢主梁上,此举能够提高双层梁单元模拟准确性。

(4)混凝土徐变时间与初始加载龄期均会对双层梁单元模拟计算结果产生较大影响。