隧道内部爆破质点峰值振速分析与预测

周亚林

(中铁十六局集团路桥工程有限公司,北京 101500)

钻爆法作为隧道开挖的主要方式,具有开挖效率高、施工快速等优点。然而炸药爆破所释放的能量只有少部分直接用于破碎岩石,大部分能量以振动、冲击波和飞石等形式产生负面效应[1]。其中以爆破振动的危害最为突出,振动过大可能破坏围岩、邻近隧道及地下建筑物。因此,控制爆破振动对保障施工安全有重要意义。

为衡量爆破振动的幅度,现行爆破安全规程以质点峰值振速(Peak Particle Velocity,PPV)作为评估指标,并对各类工程划分了安全范围。过往的研究与大量工程经验表明,毫秒延期爆破技术可有效达到降振效果[2]。毫秒延期爆破技术的关键在于其控制了多炮孔的起爆顺序,使炸药能量在空间、时间两个维度上分散,从而提高了炸药能量利用率,使岩石得到充分破碎。因此,毫秒延期爆破技术被广泛用于隧道爆破开挖,准确预测隧道内部质点峰值振速可为延期时间确定、孔网参数调整等提供有效的依据。

在隧道爆破质点峰值振速的研究中,按照振动波的传播方向将其分为水平径向、水平切向和竖直方向,使用三轴振速传感器采集爆破振动波的波形,进而计算出三方向上的质点峰值振速。在工程实践中,竖直方向上的质点峰值振速通常大于其余两个方向,故多数研究以其为预测目标。从预测方法而言,萨道夫斯基公式因简洁且便于理解的形式而被广泛应用,学者们为了进一步提高它的拟合优度与预测精度,基于量纲分析提出了多种修正经验公式。虽然这类经验公式有一定的借鉴意义,但是其预测精度难以满足工程需求[3-5]。近年来,基于机器学习的模型在岩土领域展现了强大的预测能力,相较于经验公式具有实用性强、精度高等优点[6-9]。除此之外,开挖后的隧道并不稳固,亟需对拱顶、拱腰、边墙与底板的质点峰值振速特性展开分析,找出开挖后隧道的风险区域才可为后续支护工作提供理论指导。

围绕隧道爆破开挖现场开展测振工作,记录每次爆破作业的爆破参数与振动波波形,探寻开挖后隧道拱顶、拱腰、边墙与底板的质点峰值振速的分布特性,在此基础上使用萨道夫斯基公式与极端梯度提升树(Extreme Gradient Boosting,XGBoost)分别建立质点峰值振速预测模型,并对比它们的预测精度与拟合优度,从而验证预测模型的可行性。

1 工程试验

1.1 工程概况

研究依托的工程为小西库隧道。小西库隧道为分离式隧道,总长1 247 m,其中隧道左幅全长557 m,右幅全长690 m,断面尺寸宽14.1 m,净高11 m。隧道以上元古界蓟县系雾迷山组基岩地层为主。地层中主要含硅质条带细晶白云岩与叠层石粉晶白云岩,岩体节理发育,以Ⅴ级围岩为主。隧道掌子面采取三台阶分段起爆的方式,上中下台阶间的延期时间设为50 ms。

1.2 现场测振试验

为准确测量爆破振动波的波形,采用中科测控生产的TC-4850爆破测振仪作为现场爆破振动波采集系统,该款测振仪的采样频率为1～50 kHz,频响范围为5～500 Hz;记录精度为0.01 cm/s。由于旨在分析开挖后隧道的质点峰值振速分布特征,故现场测点离掌子面距离较近,考虑隧道内部的结构特征,并避免削波现象,选用TCS.B3低频宽带三维振动速度传感器采集振动信号。传感器采集的振动信号以电信号形式传输给测振仪,测振仪对电信号进行转换处理并存储,从测振仪导出数据用电脑端软件进行爆破振动波形分析。

试验的采集频率设定为2 000 Hz,触发延时为-100 ms。为准确记录爆破振动波形,依次在拱顶、拱腰、边墙与底板共四个位置上布置测点。其中,底板测点布置于隧道底板的中线上,拱顶测点使用卡扣将传感器与隧道刚性连接。

2 隧道内爆破质点峰值振速分布特征

试验共记录了19次爆破试验、76条爆破振动有效波形数据。鉴于试验在三方向、四测点下进行,质点峰值振速的待分析因素过多,可首先分析三方向上的质点峰值振速是否有明显差异。图1为三方向质点峰值振速的概率密度分布对比图。从图中可看出,水平径向与水平切向的爆破质点峰值振速分布较为接近,竖直方向的质点峰值振速分布与其余两个方向有明显差异。此外,竖直方向的质点峰值振速均值大于其余方向,且分布得也更为离散。

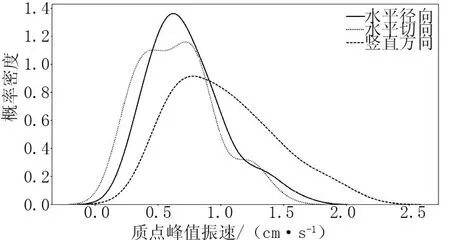
图1 三方向质点峰值振速概率密度分布

表1列出了三方向质点峰值振速的统计量,竖直方向上质点峰值振速的统计量均大于其余两方向,然而其方差较大,并不能直接得出竖直方向与其余方向有显著性差异的结论。为进一步验证差异的显著性,采用威尔科克森秩和检验[10],检验的结果如表2所示,在显著性水平为0.05的条件下,水平径向与水平切向间的质点峰值振速并无显著差异,而竖直方向与其他两方向的质点峰值振速统计意义上的显著差异。

表1 三方向爆破质点峰值振速统计量

表2 三方向爆破质点峰值振速差异显著性检验结果

鉴于竖直方向上的质点峰值振速与其余两个方向显著不同,且最大值、平均值均较大,为了保障开挖隧道的稳定性,需重点关注竖直方向上的质点峰值振速特性。基于上述考虑,图2对比了竖直方向上测点之间的质点峰值振速概率分布密度,拱腰与边墙的爆破质点峰值振速分布较为接近,拱顶与底板的分布更为相似。拱腰与边墙的爆破质点峰值振速均值小于拱顶与底板,从分布的形态而言也更为集中。可认为拱腰与边墙的爆破质点峰值振速属于一类,拱顶与底板归为第二类。

图2 竖直方向各测点质点峰值振速概率密度分布图

表3列出了竖直方向上各测点质点峰值振速的统计量,可看出拱顶与底板的统计量接近、拱腰与边墙的统计量相差较小。为验证各测点质点峰值振速分组的合理性,采用威尔科克森秩和检验做进一步分析,检验的结果如表4所示,在显著性水平为0.05的条件下,拱顶与底板并无显著差异,拱腰与边墙也无显著差异。同时,拱顶与底板分别与拱腰与边墙均有显著差异。

表3 竖直方向各测点爆破质点峰值振速统计量

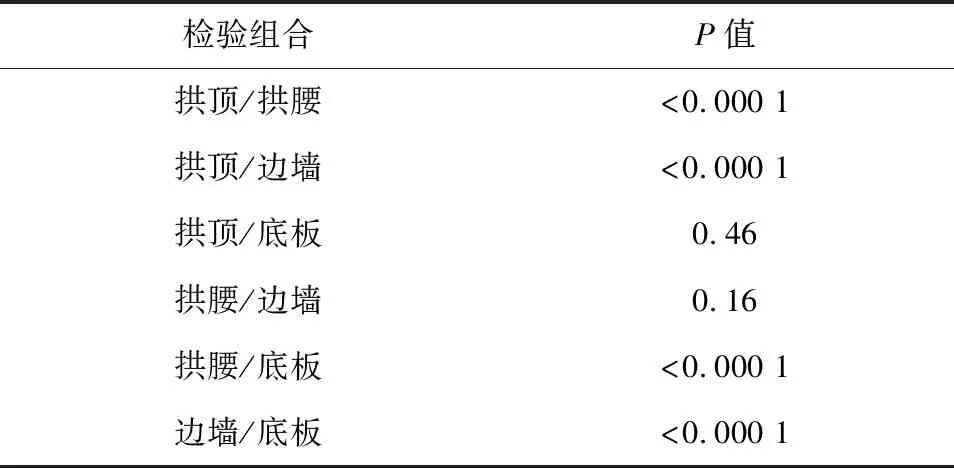
表4 三方向爆破质点峰值振速差异显著性检验结果

从上述结果可知,竖直方向上拱顶与底板的爆破质点峰值振速特性一致,拱腰与边墙的特性无显著差异,故可将竖直方向上测点数据归为两类,供后续研究使用。

3 隧道内爆破质点峰值振速预测

从前文可知,竖直方向上的爆破质点峰值振速显著大于水平径向与水平切向,且竖直方向上拱顶与底板的分布可归为一类,拱腰与边墙归为另一类,故针对竖直方向上的爆破质点峰值振速分别建立预测模型。首先使用回归方程对萨道夫斯基公式进行拟合,随后建立XGBoost预测模型,并对比两种模型的拟合优度与预测精度。

3.1 模型验证方法与评价指标

由于爆破质点峰值振速为连续性变量,为了评估不同模型的优劣,选用拟合优度R2作为模型评估指标,其定义为

(1)

此外,为客观验证模型预测的精确度,从总体数据集中随机抽取30%作为测试集,余下70%数据作为训练集。

3.2 萨道夫斯基公式拟合与预测结果

在隧道工程现场应用中,主要用萨道夫斯基公式作为爆破质点峰值振速预测经验公式,其形式为

(2)

式中:v为爆破质点峰值振动速度,cm/s;Q为单段最大装药量,kg;R为爆心距,m;K、α为与地形和地质条件有关的系数。

对式(2)两侧取对数,可得

(3)

基于现场试验测取的爆破质点峰值振速数据,对公式(3)进行最小二乘法拟合,结果如表5所示。拱顶与底板模型的测试集R2较之于拱腰与边墙模型高了17.9%,说明萨道夫斯基公式对拱顶与底板的质点峰值振速特性拟合程度不佳,预测精度难以满足现场工程应用的需求。

表5 萨道夫斯基公式拟合结果与测试集R2

3.3 极端梯度提升树模型(XGBoost)与预测结果

XGBoost是作为梯度提升决策树的一种改进算法,具有更高的预测精度、支持并行处理等优点[11],主要思想是利用决策树迭代训练以得到最优模型,其优化目标函数ObjT(x)为

ObjT(x)=L(y,fTt(x))+Ω(fT(x))

(4)

式中:y为质点峰值振速真实值,cm/s;L为损失函数;Ω为复杂度函数;fT(x)为T颗决策树的累加模型。

进一步地,定义复杂度函数

(5)

式中:M为决策树叶子个数,个;Wj为第j片叶子的输出值;γ为收缩系数;λ为约束系数。

以装药量Q和爆心距R为自变量,爆破质点峰值振速v为因变量建立XGBoost模型。XGBoost算法中包含多个超参数,如决策树个数、学习率、收缩系数等,故采用网格搜索法及交叉验证[12]以确定最终模型的超参数。表6为XGBoost经过三折交叉验证后R2最高的超参数组合。

表6 XGBoost最优超参数组合

基于现场试验测取的爆破质点峰值振速数据建立XGBoost模型,结果如表7所示。拱顶与底板XGBoost模型的测试集R2较之于萨道夫斯基公式提高了45.3%,拱腰与边墙XGBoost模型的测试集R2较之于萨道夫斯基公式提高了16.7%,以上结果表明XGBoost模型可捕捉爆破质点峰值振速特性,具有更高的预测精度,可满足工程应用的精度需求。

表7 XGBoost测试集R2

4 结 论

通过记录测取小西库隧道爆破开挖现场的爆破参数与振动波形,分析了隧道内部爆破质点峰值振速的分布特性,建立了隧道内部爆破质点峰值振速预测模型,主要结论如下。

(1)竖直方向上的质点峰值振速与水平切向、水平径向的质点峰值振速有统计意义上的显著差异,且竖直方向上质点峰值振速的最大值、平均值均较大,为了保障施工安全,应着重分析竖直方向上的质点峰值振速特性。

(2)竖直方向上拱腰与边墙的爆破质点峰值振速经检验后可归为一类,拱顶与底板属于第二类。其中拱顶与地板爆破质点峰值振速的最大值、平均值等均显著大于拱腰与边墙的爆破质点峰值振速对应统计量。

(3)基于萨道夫斯基公式的拱顶与底板组合、拱腰与底板组合在测试集上的R2分别为0.64与0.78。基于XGBoost的拱顶与底板模型、拱腰与底板模型在测试集上的R2分别为0.93与0.91,相较于萨道夫斯基公式R2分别提高了45.3%与16.7%。XGBoost模型实现了隧道内部爆破质点峰值振速的精准预测,可满足工程现场的应用需求。