二维硼结构中条带状空位长程有序分布的理论研究*

徐诗涵 何长春 杨小宝

(华南理工大学物理与光电学院,广州 510640)

在二维硼结构中,有序分布的高浓度空位可以增强其结构的稳定性,并对材料性能产生显著影响.根据最近的实验进展,本文重点关注二维硼结构中空位呈条带状分布的体系,提出有效模型系统研究结构稳定性随空位分布的变化.结合第一性原理计算结果,对空位不同近邻作用参数进行拟合,预测了不同空位浓度的稳定结构,发现在该体系中空位不同近邻存在竞争,导致长周期分布的趋势,揭示了不同近邻作用的相互竞争导致长周期结构稳定存在的关键机制.

1 引言

根据价键理论(valence bond theory)可知[1],原子的价电子数目影响原子间的成键方式,而空位的出现可以调制体系的稳定性和材料性能.在过渡金属碳化物和氮化物中,空位通过影响d 轨道键合态,从而对体系的机械性质产生影响[2].对于典型的非化学计量系统 Sc12-x□xS 体系,高浓度空位会减少体系中电子反键态的数量从而提高结构的稳定性[3].在二维硼烯中,稳定的结构被预测为平面三角晶格中由原子和六边形空位构成的准二元合金,不同的空位分布影响硼烯在电子性质、硬度、光学性质等方面的表现.因此,研究硼烯中的空位分布将拓展硼烯在纳米器件、传感器、储能材料、光学器件等领域的潜在应用[4].

理论方面,来自耶鲁大学的Ismail-Beigi 教授课题组[5]和清华大学倪军教授课题组[6]各自独立提出一种三角晶格和六边形空位混合的二维硼烯结构模型,这种模型相当于在原有三角晶格上挖去硼原子.随后,研究人员借助全局优化算法预测出硼α 和β 系列里最稳定的硼单层结构[7].硼烯结构的热力学稳定性不高以及其固有的多态性给实验制备带来诸多挑战,需要选取合适的衬底来增强硼烯结构的稳定性[8].计算表明,不同衬底对硼结构的空位分布有显著的影响: 在Al(111),Mg(0001)和Ti(0001)衬底上可以生长出六角蜂窝状硼烯[9];在Ag(111)和Au(111)衬底上可以合成不同空位浓度、分布的二维硼结构[10];硼原子在Cu(111)衬底上沉积可以形成团簇并过渡到硼烯,将在实验中存在较好的可行性[11].基于第一性原理的集团展开方法和表面结构搜索方法,研究人员预测在 Au,Ag,Cu,Ni 金属衬底上可以形成稳定单层二维硼烯[12].

实验上,使用超高真空分子束外延技术(简称MBE 方法),最先在真空环境的Ag(111)表面上成功生长出二维硼结构[8,13].Feng等[13]在纯净的Ag(111)表面上生长出单层硼烯结构,其中在Ag(111)表面生长的S1 和S2 相分别与理论计算的β12(ν1/6)和χ3(ν1/5)结构模型一致.在Ag(110)和Ag(100)表面上也可实现单层硼烯的生长,其中在Ag(110)表面主要有χ3(P1),β(P2,P3)和β8(P4)四种相[14].在Ag(100)表面上,生长出的单层硼烯结构可以看作是不同浓度硼结构按照一定比例组成的混合长程有序相,其中A相是由β12:χ3=2:1混合而成,B相是β12纯相,C相是β12:χ3=1:2混合[15].此外,实验人员分别在Al(111)上生长出六角蜂窝型硼烯[16]、在Cu(111)生长出χ3相的六方孔洞混合结构[17]、在Ir(111)生长出χ6相的六方孔洞结构[18]、在Au(111)上生长出理论模型为ν1/12的单层硼烯结构[19].

在硼烯结构中,空位浓度经常高达1/9—1/4,其分布情况非常复杂,对材料的性能有着更加显著的影响.在之前的研究中,我们提出了基于α硼平面结构的自组装通用规律,发现基于自组装的空位分布有利于提高单层硼烯结构稳定性[20].本文重点关注实验中观测到的具有长周期的硼结构,将二维硼结构空位分布简化为由点空位组成的条带状硼链,探究空位与空位之间的相互作用对体系结构稳定性的影响.根据硼原子成键特征产生合理的候选结构,并借助第一性原理计算得到总能,通过对不同近邻作用进行能量拟合,对不同空位浓度的结构进行进一步的筛选预测.在轴向次近邻伊辛(axial next-nearest-neighbor Ising,ANNNI)模型中,最近邻和次近邻之间相互竞争会导致体系出现长程有序性[21].根据空位有效作用模型,二维硼结构具有形成长周期结构的趋势,与第一性原理计算所得到的结果相符.该模型能够对包含带状空位的硼烯结构稳定性进行预测,并揭示了不同近邻作用的相互竞争导致长周期结构稳定存在的关键机制.

2 计算方法

寻找稳定的硼烯结构需要对结构的总能进行评估,本文采用基于密度泛函理论第一性原理计算方法,使用的是VASP (Viennaab initiosimulation package)软件进行总能计算,选择Perdew-Burke-Ernzerhof (PBE)泛函的广义梯度近似处理电子的交换关联作用.考虑到硼烯是二维结构,沿垂直平面方向加入 20 Å 的真空层避免周期性边界条件导致的镜像相互作用.在对截断能和k点进行收敛性测试后,选取 374 eV 的截断能,以及任意两个k点的间隔小于 0.1 Å-1,设置总能收敛标准为 10-5eV,力收敛标准为 10-2eV/Å对初始结构进行充分弛豫.当候选结构数目过多或者结构尺寸太大时,直接使用第一性原理计算所需要的计算成本太大,有必要预先排除掉部分不合理的结构以提升计算效率.针对条带状空位分布结构建立模型,采用设定一系列条件限制对其进行结构筛选,通过对结构中空位之间不同近邻作用参数拟合,对结构能量进行快速评估.

实验中观察到的二维硼烯可以看作是不同空位浓度的结构模块拼接而成,本文提出空位有效相互作用模型来描述此类结构的稳定性.实验中观察到的条状空位硼烯结构如图1(a)所示纵向切割拼接.如图1(b)所示,横向上将该结构变为一个如图1(c)的等效结构,其中实心绿色点代表硼原子,空心点代表空位.将不同空位分布对总能的影响等效为空位之间的相互作用,每个结构的能量可以用不同近邻作用总和表示为

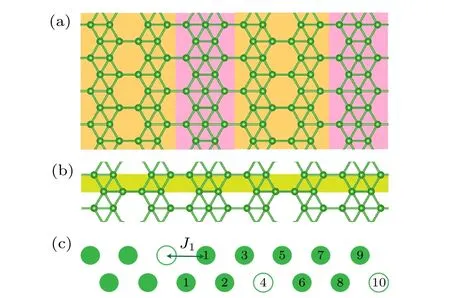
图1 (a)在Ag(100)表面生长出的A 相的理论模型结构;(b)将该结构从横向看作是一个包含点空位分布的条带硼链;(c)上述条带硼链的模型示意图,其原胞为包含3 个空位的16 个原子位点的结构,其中空点圆代表空位,实心圆代表硼原子,对于最左边的空位,用数字标出其不同近邻的位置Fig.1.(a) Theoretical model structure of phase A grown on the Ag(100) surface;(b) a lateral view of the structure as a strip boron chain containing a distribution of point vacancies;(c) a schematic representation of the strip boron chain model,with a unit cell consisting of 16 atomic sites,including 3 vacancies.The point vacancies are denoted by open circles,while the boron atoms are represented by solid circles.For the vacancy on the far left,the diagram has been annotated with numbers to indicate its various neighboring positions.

其中J0是参考能量常数,Ji代表第i近邻对总能的贡献值,ni代表体系中第i近邻作用的个数.

在进行结构总能计算之前,需要对所有候选结构进行初步筛选排除掉重复的、不合理的结构.空位浓度范围为η=m/n,其中n和m分别为晶胞中的位点和空位数目,含有n个位点的二维硼烯有2n种可能结构.借助本课题组自主开发的程序SAGAR (structures of alloy generation and recognition)[22]可以去掉重复结构,但随着体系晶胞包含原子增多,可能的候选结构数目将急剧增长.本文结合硼原子成键特征设定限制条件对结构进行进一步筛选: 1)规定空位与空位不能产生第一近邻(保证形成的是六边形空位);2)排除空位之间的第二近邻(保证不会出现配位数是3 的硼原子);3)排除空位之间的第七近邻(防止硼原子过多聚集).将结构的空位分布情况表示成二进制数,按照限制条件进行结构检查和筛选.加上限制条件后,遍历筛选出的结构数目大幅度下降.例如在包含32 个原子的晶胞中引入6 个空位,在筛选前结构数目为4.295 × 109,经过筛选后得到93 个候选结构.考虑到计算成本,本文选择最大晶胞包含48 个位点,得到的候选结构空位浓度范围为η ∈[1/7,1/4] .

3 结果分析

以实验中空位浓度为3/16 系列结构为例,根据筛选条件得到候选结构,并结合第一性原理计算结果拟合模型参数,进一步研究晶胞更大的体系;针对长周期趋势,选取浓度1/6 系列结构进行详细计算分析,根据近邻系数的变化,探究近邻相互竞争对结构趋于长周期分布的关键作用.

3.1 参数拟合快速评估

在有效相互作用模型下,不同空位分布的硼烯结构的能量表示为不同近邻作用的总和,相应的结构用对应的近邻统计序列表示.在经过条件限制和对称操作后,在包含32 个原子的晶胞中引入6 个空位的体系共有93 个候选结构.对这些结构进行第一性原理计算其总能后,再根据各自的近邻统计序列拟合出每一个近邻对于能量的贡献值.对于空位浓度η=6/32 的结构,拟合后得到的近邻作用参数J2—J10分别为4.9474,3.4886,2.1270,1.1765,-0.0800,-0.1012,-0.1076,-0.1111,-0.1054,空位相互作用对总能贡献值从第6 近邻开始收敛.为了能够更好地描述该浓度系列稳定结构近邻统计的变化规律,将近邻截断范围选取到第10 近邻.这组参数同样可以描述其他不同空位浓度结构的稳定性,其拟合总能与其第一性原理计算所得的总能相关性如图2(a)所示.在随机选取空位浓度下,使用参数拟合的结果能够与第一性原理计算总能具有较好的相关性.对于空位浓度η=3/16 的结构,其拟合计算得到的稳定结构如图3(a)所示,与实验中在Ag(110)表面上得到的长程有序单层硼烯结构一致.使用参数模型评估稳定性并进一步筛选时,尽管会有部分能量简并的结构出现,但是候选结构数目明显下降,有效节约了后续进行第一性原理计算的时间成本.

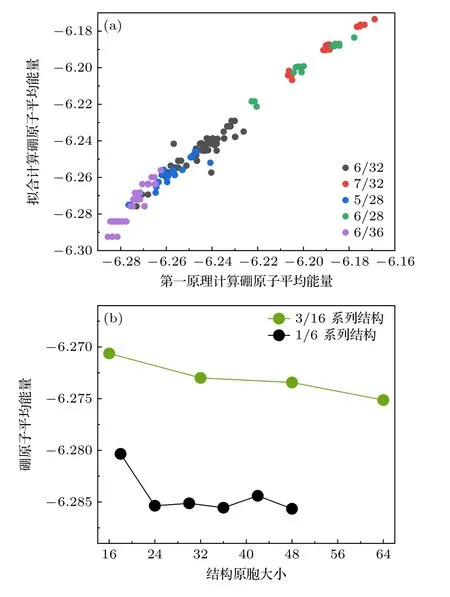
图2 (a)参数拟合计算和第一性原理计算的相关性图像,其中不同颜色的点代表不同空位浓度的候选结构;(b)第一性原理计算下3/16 和1/6 系列结构随着原胞大小变化的硼原子平均能量趋势图Fig.2.(a) Correlation plot between parameter fitting calculations and first-principles calculations;(b) trend graphs of average energy of boron atoms in structures of 3/16 and 1/6 under different cell sizes,as calculated by first-principles methods.

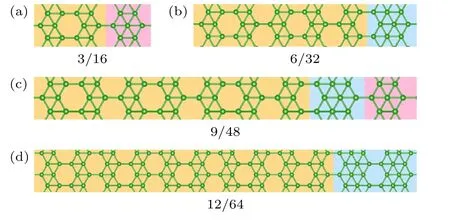
图3 (a)—(c)分别为在第一原理计算下3/16 系列结构不同原胞大小下的稳定结构,同时也是参数拟合计算所指向的稳定结构;(d)构造原胞大小为64 的3/16 系列结构Fig.3.(a)-(c) Stable structures of the 3/16 series under different cell sizes obtained through first-principles calculations,which are also the stable structures indicated by parameter fitting calculations;(d) artificially constructed structures of 3/16 with a cell size of 64.

表1 4 个相同浓度结构的近邻统计数目Table 1. Neighbor count for four structures at the same concentration.

3.2 空位分布的长周期结构

如图4(a)—(f)所示,随着晶胞尺寸的增大,其稳定结构中空位的分布随之变化.根据参数拟合的结果,在此浓度下第4,5,6 近邻对于总能的贡献占比最为突出.随着原胞尺度的增大,图4(g)中第4,5,6 近邻统计数目也呈现一定的规律,可以使用[n4n5n6]和[J4J5J6]去描述结构的能量和结构.平均能量=E/Natom,Natom为结构中硼原子的数目,稳定结构对应的近邻分布如表2 所列.对于第i个结构(i=1,2,3,···,n,结构中包含的硼原子数Natom=5(i+2)),当仅考虑第4,5,6 近邻时,结构的平均能量为

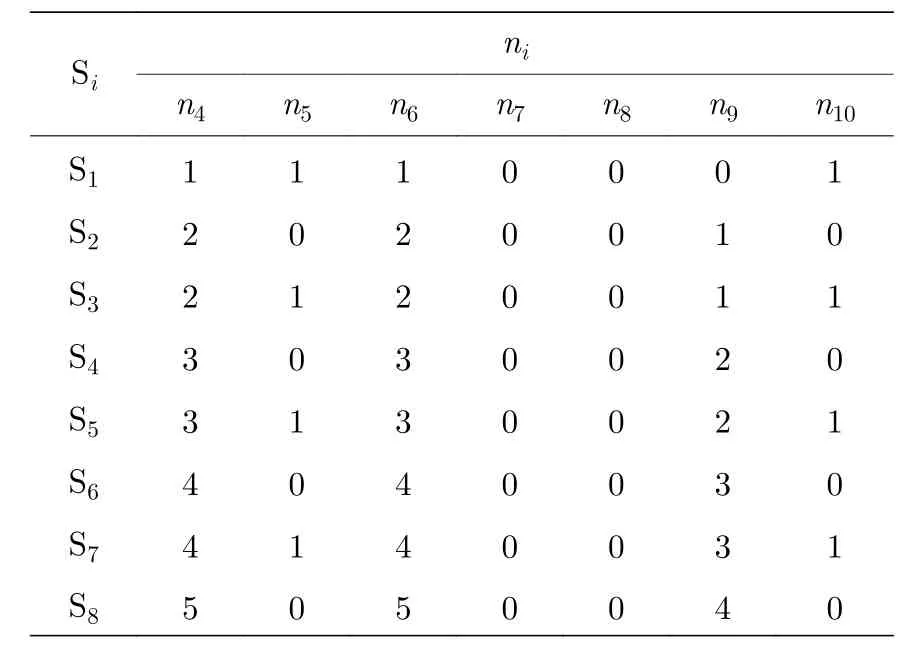
表2 不同原胞大小、浓度相等的稳定结构近邻统计数目Table 2. Neighbor count for stable structures with equivalent concentrations at different cell sizes.

图4 (a)—(f)分别为1/6 系列结构不同原胞的稳定结构.每个结构的原胞大小分别表示在每个结构图的左上角;(g) 1/6结构随着原胞大小变化的硼原子平均能变化图,绿线代表拟合计算过程中只选取第4,5,6 近邻结果,黑线代表拟合计算过程近邻范围截取到第10 近邻结果Fig.4.(a)-(f) Depict stable structures of the 1/6 series with different cell sizes.The cell size for each structure is indicated in the top left corner of each respective structure diagram.(g) Average energy variation of boron atoms in the 1/6 structure as a function of cell size.The green line represents the fitting calculation process with only the 4th,5th,and 6th nearest neighbors considered,while the black line represents the fitting calculation process with the neighbor range truncated to the 10th nearest neighbor.

根据(2)式,此时体系的平均能量变化趋势如图4(g)绿色折线所示.随着原胞尺寸的增加(从18 个原子位点到312 个原子位点),其呈现下降的趋势并且收敛于-6.28115 eV/atom,最小原胞呈偶数倍的结构能量一致,这是因为进行能量评估的近邻作用只选取了J4,J5和J6.从表2 可以看到,1/6系列结构的稳定结构的近邻统计呈现出非常明显的变化规律,可以构造出更长周期的稳定结构.对于该空位浓度的系列结构,当选取的近邻范围扩展至第10 近邻时,第i个结构的平均能量E为

当加入更高阶近邻作用时(扩展至第10 近邻),其平均能量随着原胞尺寸的变化如图4(g) 黑色折线所示.通过浓度1/6 系列结构,本文模型能够与第一性原理计算平均总能如图2(b)绿色折线的变化趋势相符.随着原胞尺寸的增大,体系平均到每个硼原子的拟合能量趋于-6.2907 eV/atom.平均能量在振荡中降低,幅度逐渐减小,最终趋于平稳.平均能量收敛的常数主要来自于第4 近邻和第6 近邻作用的贡献,第9 近邻和第10 近邻对平均能量有贡献,使得原胞大小为最小原胞偶数倍的结构平均能量逐步降低,这是出现长周期结构的主要原因.

4 结论

本文考虑带状空位分布的二维硼烯,通过一系列限制条件排除不合理和重复的结构,提出了空位有效相互作用模型.并结合第一性原理计算拟合不同近邻的空位相互作用系数,进一步应用于结构预测.计算表明,在空位浓度相等的情况下,体系中的空位分布随着晶胞尺寸的改变而变化;针对1/6 系列结构进行分析,发现其空位近邻之间对总能存在相互竞争.通过平均能量趋势很好说明了长周期结构稳定存在的原因.