矩阵奇异值分解与非齐次线性方程组系数矩阵的广义逆求解
2024-05-13邵广周
吴 华, 邵广周
(1.长安大学 理学院,西安 710064; 2.长安大学 地质工程与测绘学院,西安 710054)
0 引 言
在实际线性反演问题中,对于任意非齐次线性方程组Ax=b有解,则称其为相容的,否则称之为不相容或矛盾的.广义逆理论把求解任意非齐次超定、欠定或混定线性方程组的解全部概括统一起来[1].如果能够找到其系数矩阵A的Moore-Penrose逆A+,就可得到问题对应的解.由于A+存在且唯一,所得的解x=A+b也是唯一的[2].矩阵广义逆在解线性方程组、矩阵方程组中有着广泛的应用,文献[3]通过研究相关矩阵方程的性质找出了解存在的条件.文献[4]基于内积理论对线性矛盾方程组最小二乘解问题进行了理论推导.本文则从矩阵奇异值分解算法着手,给出非齐次线性方程组的自然解.
1 矩阵奇异值分解
对任意秩为p的m×n阶矩阵A,可分解成如下形式[5]
(1)
其中,Λ为对角矩阵,对角线元素λ1,λ2,…,λp为正的非增序列,其平方是矩阵ATA和AAT的p个非零特征值,称对角线元素λi为奇异值.U和V分别为m×m和n×n的正交矩阵,对应的特征向量相互正交(即UUT=UTU=I,VVT=VTV=I),U对应的特征向量张成数据空间.V对应的特征向量张成模型空间.

其中,Up,Vp分别为U,V的前p列,则可将A写为
(2)
由(2)式知,在进行奇异值分解后,矩阵A可用不含零特征值向量U0和V0的矩阵的乘积来表示,可见奇异值分解是把数据空间和模型空间分解为非零空间和零空间两部分.非零特征值对应的特征向量Up和Vp张成非零空间,U0和V0则张成零空间.
现以正交矩阵U为例进一步说明奇异值分解的作用,考查Up和U0的性质以及彼此之间的关系:
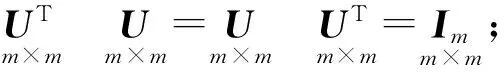






类似地,矩阵V,Vp和V0也具有上述性质.
2 非齐次线性方程组的自然解

3 奇异值分解算法实现
3.1 Householder变换
奇异值分解是一种正交变换,算法实现时可通过一系列正交变换来完成,其关键算法是Householder变换,该算法可将矩阵A对角化[6].
Householder变换最关键的步骤是如何构造正交矩阵Q(满足QQT=QTQ=I),具体可按下式来实现:
(3)
其中,u为任意非零向量.显然,QT=Q,则
表明Q是一个正交矩阵,称矩阵Q为Householder矩阵.接下来的问题是该如何选择u.
现设一个已知的n维非零向量为v,存在正交矩阵Q使得
Qv=-sign(v1)‖v‖e1,
(4)
其中,e1为单位向量基,即e1=[1,0,0,…,0]T.sign(v1)表示取向量v的第一个元素的符号,即

则向量u可按下式构造
u=v+sign(v1)‖v‖e1.
(5)
将(5)式代入(3)式所得到的矩阵Q就能够满足(4)式.现通过如下例子进行证明.
例对于列向量v=[1,3,4,3,1]T进行Householder变换.
解① 构造向量u:
u=v+sign(v1)‖v‖e1=[1,3,4,3,1]T+1·6·[1,0,0,0,0]T=[7,3,4,3,1]T;
② 计算uuT和uTu:
③ 计算正交矩阵Q:
④ 计算Qv:
⑤ 根据式(16)计算Qv:
Qv=-sign(v1)‖v‖e1=-1·6·[1,0,0,0,0]T=[-6,0,0,0,0]T.
上述算例表明,对于任意向量v,按照(5)式构造向量u,再按照(3)式构造矩阵Q,然后左乘以向量v,即可将向量v映射到单位向量基e1上.也就是说,可将向量v转变为第一个元素等于sign(v1)‖v‖,而其余元素均为零的向量.
3.2 奇异值分解编程算法步骤
(i)首先利用Householder变换把矩阵A逐步转换为双对角阵.设U1为一个Householder矩阵,将U1左乘以A,将其第一列元素化为除第一个元素之外其他元素全为零的向量.现以一个6×5的矩阵A为例,考察这一过程:
(6)
再设V1也是一个Householder矩阵,将其右乘以矩阵U1A,可将(6)式中用圆圈表示的元素化为零,即
同理,采用上述方法逐步选择Householder矩阵U2和V2,把(6)式中用圆圈表示的元素化为零.当A被左乘五次、右乘三次时,就变成了双对角阵
对于一般的m×n矩阵,利用Householder变换可逐步将其化为如下双对角矩阵:
其中
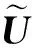
由于右乘变换矩阵Vj后又会将上一步的计算结果矩阵左下角已被化为零的元素转换为非零元素,通常不能用Householder变换一次性将矩阵A化为对角矩阵.
(ii) 接下来,再采用一系列平面旋转变换把上一步得到的双对角矩阵B逐次化为对角矩阵Λ,其中Λ为奇异值矩阵.列旋转变换矩阵的构造可按如下步骤进行:
首先构造如(7)式所示的矩阵V12,右乘以矩阵B.
(7)
其中
并计算BV12.
再构造如(8)式所示的矩阵U12,左乘以矩阵B.
(8)
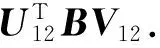
同理,构造平移旋转矩阵

构造平移旋转矩阵

逐次迭代可得
最后,将奇异值按非增序列排序,在上述迭代过程中,如果某个次对角线元素|ej|≤ε,可将ej看作为0.如果对角线元素|sj|≤ε,可将sj看作为0,即此时奇异值为零,其中ε为精度要求.

4 结 论
本文给出了非齐次线性方程组的奇异值分解算法,通过Householder正交变换将方程组系数矩阵A逐步迭代变换为对角矩阵,从而得到系数矩阵的奇异值,进而得到非齐次线性方程组的自然解,该方法使得非齐次线性方程组的求解更容易进行计算机编程实现.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.
