融入体育元素的高等数学教学模式探索与实践——以“曲率”为例

苏新华, 葛焕敏, 沈燕飞

(北京体育大学 体育工程学院 中国体育大数据中心,北京 100084)

0 引 言

在如今大数据时代下,新型智能体育人才的培养是实现智慧体育场馆、智能体育健身和互联网+健身等科技创新的关键.其中,人工智能和工程创新的基石在数学,其稳行致远的前提是解决好数学的基本问题.因此,强调大学数学教育在体育科技人才方面的引导作用至关重要[1-5].

高等数学作为理工科学生的基础必修课程,是后期工科课程的基础.目前,不少高校通过线上线下、翻转课堂和小组讨论等方式实行高等数学教学形式改革并取得了一定的成效[6-14].其中,以“曲率教学设计”为例,文献[11]探究了如何将传统教学与微课教学有序衔接,文献[12]探索了基于活动-过程-对象-图式(Action-Process-Object-Scheme,简称APOS)的教学新模式,文献[13]探究了信息化教学模式下微课的应用,文献[14]探讨了高等数学教学结构的宏观设计和微观设计的内容和方法等.但是,目前高等数学教学内容中鲜有涉及体育教学案例的分析与应用.然而,基于实际体育赛事及实际工程的案例教学,对于“体育强国”战略驱动下创新型智能体育人才的培养具有重要的意义.

本文以融入体育元素的“曲率”教学设计为例,将我国冰雪运动重点突破项目——短道速滑引入课堂,极大地激发了学生的学习兴趣.给出曲率与汽车弯道行驶和工业制造的实际生活案例,体现了曲率的广泛应用.充分考虑学生专业特色,提出合理有趣的案例,避免了课本案例的千篇一律,进一步拓宽了学生的视野,提升了学生的专业认知.同时,基于曲率与导数、极限等内容具有强关联性,授课时通过层次引导激发了学生的求知欲,有助于培养学生的自主学习习惯和学习专注力.此外,课堂设计中案例的首尾呼应,激发了学生思考课前案例引入,引导学生利用所学知识进行课尾案例分析,激发了学生的学习创造力与解决实际问题的能力.总的来说,精彩合适的案例教学设计展现了课堂思政教育,使其产生润物无声的效果;层次引导教学培养学生从无到有的新思想产生,激发学生不断探索的欲望;案例应用中让学生及时感知自己所学知识的实际应用价值,增强报国之志(图1).

图1 基于体育工程案例的高等数学课堂思政教学设计

1 融入课程思政的“平面曲线的曲率”教学设计

1.1 案例引导与分析——提出问题

曲率为学生新接触的一个概念,通过具体案例分析,让学生直观感受曲率的物理意义是用来衡量曲线的弯曲程度.同时,感知曲率在实际工程实践中的重要应用.具体案例包括两方面:

1.1.1 曲率与向心力之间的关系

(i) 速滑中的转弯

课堂上播放武大靖在美国短道速滑世界杯中的夺冠视频,同学们观看的热血沸腾,深深地感受到了中国竞技体育中的辉煌成就(图2).在培养学生民族自豪感的同时,引导学生思考问题:武大靖在速滑比赛中,观察直道与弯道滑行的体态差异与速度差异,其大致原因是什么?

图2 武大靖短道速滑

学生发现,在直道滑行时体态是直立的,而在弯道时需要向滑行曲线凹的一侧大幅度倾斜身体.直观感知原因为:在弯道时需要通过侧身的方式增加运动所需要的向心力,防止离心作用力引起的外弹.也就是说,理想情况下,在速度v不损失的情况下,弯道滑行时所需要的向心力增大.假设用K来表示弯道的弯曲程度,那么向心力F与K为正相关,即F∝K.

(ii) 开车中的弯道行驶

在弯道开车时需减速慢行,避免发生交通事故.通过播放汽车在弯道行驶过程中因超速而造成交通事故的视频,提醒学生在自己及家人朋友驾驶中要时刻遵守交通法规,珍爱生命,减速慢行.同时,引导学生们分析事故发生的原因,汽车在高速状态下进行弯道行驶,此时所需要的向心力增大.然而,当地面支撑力和摩擦力等合力无法达到所需的向心力时,最终产生交通事故.类似于短道速滑案例分析,可知向心力F与K为正相关,即F∝K.

通过分析上述两个案例,初步得到结论,在速度不变时,向心力F与曲率K正相关.而同学们都清楚向心力F与运动半径R负相关,进而导出1/R∝K.其中,半径R与K的准确关系为本节内容的教学重点.

1.1.2 曲率与工业制造的关系

挖掘高等数学等基础学科在工程研究中的应用,让学生直观感受所学知识的实用性,可以激发学生的学习热情,重视基础学科的学习,为将来科技报国奠定基础与信念.本节课中,通过器件曲面加厚阐述了工业制造与曲率的密切关系(图3).具体而言,制造业中常需对弧形器件进行曲面加厚,其加厚度以曲率最大的那段弧形为标准.这都与曲率的知识密切相关.

图3 工业制造中的曲率

1.2 知识关联与讲解——分析问题

了解曲率的相关应用之后,开始曲率知识的系统性学习.要清楚上述案例发生的原因,需要解决两个问题:(i)曲率如何计算;(ii)曲率与曲线半径之间的关系是什么?

学生们已经清楚曲率是用来衡量曲线弯曲程度的量.通过绘制曲线,让学生感知影响曲线弯曲程度的因素包括两因素:曲线的切线转角(见图4(i))和曲线的弧长(见图4(ii)).

图4 曲线弯曲程度度量

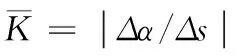
启发提问2:目前,平均弯曲程度和平均速度运用了类似的思路.那么,结合在某点瞬时速度和平均速度的关系,推测曲线上某点M的曲率如何计算?

至此,通过对相关知识点层层递进,引导学生自主推导得出计算曲线一点处的曲率公式

(1)

由上述曲率公式(1)知,直线的曲率为0,即直线是不弯曲的.对于半径为R的圆,圆上各点的弯曲程度均匀对称,利用圆弧与圆心角之间的关系(图5),可以得到圆上各点的曲率为

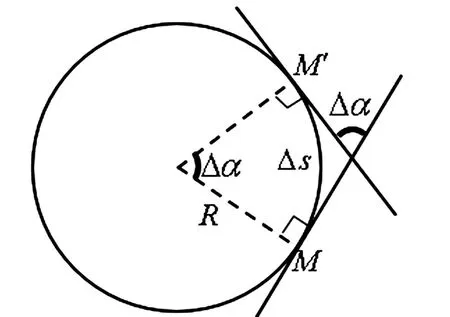
图5 圆弧与圆心角的关系

目前,学生清楚了直线与半径为R的圆上点的曲率.那么,对于一般曲线的曲率如何计算呢?观察发现,假设曲线方程满足某些条件(如二阶可导)时,K的计算关键在于dα和ds的计算.利用导数的几何意义以及《高等数学Ⅰ》微分的内容,引导学生探究dα和ds的计算公式.

启发提问3:要计算dα,需要清楚α的函数表达式.目前,与α相关的表达式是什么?对应的微分是否可得?

启发提问4:接下来要计算ds.对于曲线函数y=f(x),其弧长s与x存在函数关系s=s(x).因此ds的计算关键在于s′(x),目前s=s(x)的具体表达式未知,如何计算s′(x)?

学生反馈:可以尝试利用导数的定义进行推导.对于函数曲线y=f(x),弧长s与x的函数s=s(x)是x的单调递增函数.因此,由导数定义可得

进而有

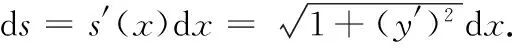
辨析与讨论:弧微分与微分之间的关联性.

微分的几何意义:用切线纵坐标的增量近似函数真实变化量,即用QT近似代替QM′(∇x→0时),公式表示为:Δy≈dy=f′(x)dx=tanαdx(见图6).

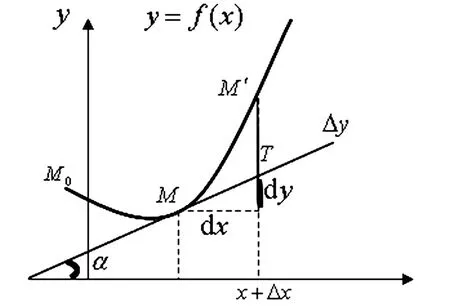
图6 微分与弧微分几何关系

弧微分的几何意义:用切线的斜边增量近似曲线中真实弧长的增长量,即用MT近似MM′(∇x→0时),公式表示为:Δs≈ds=s′(x)dx=secαdx(见图6).

至此,通过启发式教学,将学生的已学知识点与未知知识点建立联系,层次引导学生自主探究,进而推导了dα与ds的计算公式(图7).将其表达式代入到曲率计算公式中,得到曲率的计算公式

图7 导数与弧微分的知识点关联图

对于曲线而言,弯曲程度越大,所对应的曲率值越大.至此,对于曲线上各点所在邻域弯曲程度的衡量,不再是通过简单的视觉感知而给出结论,可通过曲率公式进行精确计算.

在曲率与向心力之间关系的课前案例中,分析得到了曲线在某一点的曲率K与运动半径R成反比关系.接下来,分析曲率与曲率半径之间的确切关系.

设M为曲线C上任一点,在点M处作曲线的切线和法线,在曲线的凹向一侧法线上取点D使|DM|=1/K=R(图8),把以D为中心,R为半径的圆叫做曲线在点M处的曲率圆(密切圆),R叫做曲率半径,D叫做曲率中心.

图8 曲率圆与曲率半径

注意:当K=0时,曲率半径可以认为无穷的.在M点处曲率圆与曲线有下列关系:(i)有公切线;(ii)凹向一致;(iii)曲率相同.

1.3 知识迁移与应用——解决问题

通过上述内容的学习,学生掌握了曲率的计算公式,以及曲率半径与曲率之间的关系.利用这些知识,可以解决工程中的相关问题并解释课前实际案例,培养学生学以致用的意识.

例设工件内表面的截线为抛物线y=0.4x2(图9(i)).现在要用砂轮磨削其内表面,问用直径为多大的砂轮才比较合适?

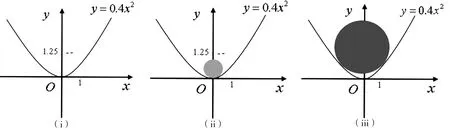
图9 不同尺度砂轮的示意图

分析 为了可以更高效地完成磨削工作,砂轮的半径需尽可能的大,这样可以避免频繁更换砂轮.同时,为了不使砂轮磨去太多,砂轮的半径又不能太大,否则曲率较大的位置砂轮无法进行磨削.通过动画演示两种情况(图9(ii)和图9(iii)),直观感知砂轮选取不合适所产生的低效性与材料浪费问题.鉴于上述分析,砂轮的半径应不大于抛物线上各点曲率半径的最小值.

解计算可得y′=0.8x,y″=0.8,将其代入曲率计算公式可得

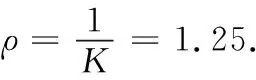
回归到课前案例,解释它们如何应用曲率的相 关知识.

(i) 曲率与向心力之间的关系

回顾武大靖短道速滑的视频分析,运动中向心力F与K正相关,即F∝K.向心力的计算公式为F=mv2/R,其中R为运动半径.结合本节课所学的曲率与曲率半径之间的关系R=1/K,可得F=mv2K,进而得出向心力与曲率之间的正比关系.依据此公式,可以解释汽车在弯道转弯时所需要的向心力增加,因此在弯道要减速慢行,减小汽车行驶所需要的向心力.

(ii) 曲率与工业制造的关系

利用曲率与曲率半径的关系R=1/K,可解释工业制造中的现象.在器件曲面加厚中,不同弧段对应的曲率半径不同,器件要实现均匀加厚,需以可增加厚度最小的那一段弧作为参照标准,即曲率半径最小的弧段作为标准(曲率最大的弧段).此外,曲率半径为曲率显示器的重要参数.理论上,为了更好地体验沉浸式与环绕感,在符合人眼生理弧度曲线的情况下,显示器弯曲的幅度越大越好,此时曲率半径越小.在汽车设计中,汽车的曲率半径越小,说明在弯道的灵活性越好,汽车机动性越好.

总的来说,通过体育和工程案例引出曲率的内容.然后,将新知识与学生已学知识进行层次关联,引导学生自主分析曲率的相关内容.最后,将所学的知识应用于实际问题和课前案例,实现教学内容的首位呼应.

2 教学效果

通过实践融入体育元素的高等数学教学设计,同学们的学习热情、学习效果与爱国之情等方面都有显著提升.为了更加客观地了解以“曲率”为例的高等数学教学模式的教学效果,针对参与这次教学实践的北京体育大学体育工程学院2020级数据科学与智能体育工程专业的学生设计了一份问卷调查(表1).通过问卷星发放调查问卷,其中79名学生参与了问卷填写.

表1 问卷调查

通过问卷结果统计,融入体育元素的高等数学教学模式显著提高了学生的学习热情和爱国之情,让学生们深刻体会到了高等数学在体育及工程领域的重要性,更加重视高等数学的学习.同时,学生对于此类课堂设计的满意度达到了95%.总体而言,此教学模式探究与实践激发了学生的学习热情,促使他们重视基础学科的学习,提升了他们对体育科技的认知,为将来体育科技强国奠定了基础与信念.

3 结 论

本文基于高等数学中曲率的教学设计,将高等数学知识与体育工程领域相结合,旨在让学生们在实际案例中感知高等数学的重要性,为培养新型体育智能人才奠定基础.在教学过程中发现,选择合适的案例进行知识导入,能激发学生的学习热情,同时在案例分析中让思政教育润物细无声地影响着学生.例如,通过播放武大靖短道速滑的夺冠视频,学生为中国竞技体育在世界的领先地位而自豪.接下来,通过启发式与关联式教学模式,让学生层次进入教学重点内容,并且积极主动的思考与讨论,进一步激发学生对于知识的探知欲.最后,运用所学知识解决工程问题与课前案例,让学生及时体会学有所用.通过知识外延引导,激发学生的创造力和报国之志.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.