旋转曲面融入课程思政的教学设计
2024-05-13毕含宇
毕含宇, 龙 薇
(江西师范大学 数学与统计学院, 南昌 330022)
0 引 言
高等数学课程是高校理工科专业的公共必修课,是学生入学后学习的第一门数学类课程,其学习情况的优劣,对大学期间后续课程的学习有着深远的影响.该课程是理工科必不可少的知识工具,是专业课程的数理基石;是科学技术发展的基础;是培养理性思维能力和科学思想方法最好的知识载体.为了扣好理工科学生的第一粒纽扣,高等数学融入课程思政是必然的,是必需的,是必要的.在已进行的高等数学课程思政研究中,既有理论认知也有实践探索,其中一些研究论文颇具代表性.如文献[1-2]是对高等数学课程思政体系的研究;文献[3-4]是对高等数学课程思政宏观策略的思考;文献[5-6]是对高等数学具体教学内容的微观思政探索.本文以实现知识转移到价值塑造的自然升华为目的,从具体教学设计出发,进行课程思政实践,取得了良好的课堂效果.
旋转曲面是常见的一种重要曲面,从生活小物到国之大器,处处存在旋转曲面的应用;从自然世界到工程技术,随处可见旋转曲面的模型.曲面是空间解析几何的重要基本内容,也是二元函数微积分学的基石,是解决问题的基本工具.此次教学内容重在体会旋转曲面的形成,掌握旋转曲面的定义和方程,描绘旋转曲面的图形.曲面教学的成功与否极大程度上决定了二元函数以及重积分教学的有效性.
本次教学设计的整体思路:通过应用实例和实验,创设问题情境,引出旋转曲面,采用丰富多样的教学手法,如启发引导法、教具展示法、分组讨论法、板书和多媒体相结合等,让学生更深刻地理解并掌握旋转曲面的定义、方程和图形.
1 教学设计概括
学生不容易接受单纯地用理论去讲解旋转曲面的定义和方程,本次教学采用“实例教学”“实验教学”“问题教学”“研讨教学”等教学方法与模式,在逐层递进的问题中引导学生领悟旋转曲面的相关知识点.
2022年北京冬奥会,我国组合隋文静、韩聪夺得花样滑冰双人滑冠军,通过播放比赛过程中的一段两人在冰上旋转的小视频,引入动态的旋转,美丽而快乐.展示常见的旋转曲面图片,小到日常生活,大到科技发展,旋转曲面无处不在.通过观看视频和图片,思考一个问题:旋转曲面是如何生成的?接着做个小实验——旋转硬币,在硬币旋转的过程中进入今天问题的探究:旋转曲面的定义和方程.认知思路从特殊到一般,让学生参与思考、分析问题,最后解决问题,得出结论,避免直接硬塞给学生定义、方程的教学.最后利用旋转曲面的定义、方程推导出生活中常见的旋转二次曲面的方程和图形,并通过分组教学,让学生亲自动手制作旋转单叶双曲面模型,从一般回到特殊,首尾呼应.本节课的思政元素融入如图1所示.

图1 旋转曲面的教学设计
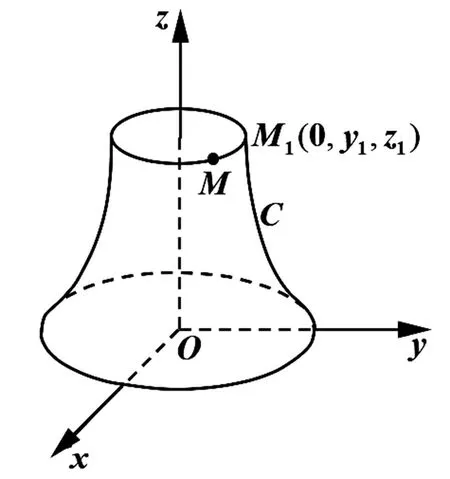
图2 旋转曲面
2 教学过程
2.1 创设情境,引入新课
首先播放一段小视频.2022年2月19日,北京冬奥会花样滑冰双人滑自由滑比赛在首都体育馆举行,我国组合隋文静、韩聪夺得冠军,并创造了双人滑最高分世界纪录.冬奥会花样滑冰双人滑金牌时隔12年再次花落中国.视频展示的是比赛中两人在冰上旋转的一段,这美丽的动态旋转中蕴含着什么数学知识呢?进而引出本次课的主题——旋转曲面.通过小视频,学生们自然能感受到奥运冠军不畏艰难、奋勇拼搏、挑战自我的体育精神;爱国爱党、为国争光的民族精神;和平、友谊、团结的奥运精神.
接着展示常见的旋转曲面的动画、图片,如花瓶、灯笼、广州塔小蛮腰、神州飞船返回舱,从日常生活到科技发展,从民族传统文化到国之大器,随处可见旋转曲面的身影.进而引出问题:旋转曲面是如何生成的?即如何用数学语言来定义旋转曲面呢?动画和图片,无需言语,让学生感受民族传统文化之美,祖国科技之先进,从而激发民族自豪感和文化自信,激发科技报国的家国情怀和使命担当.
2.2 结合实验,切入主题
为直观地体会旋转曲面的定义,组织学生们动手做实验:旋转硬币.将硬币充分旋转起来,能看到什么呢?是的,球体!球体的表面就是球面.在这个旋转的过程中,硬币外围的圆周划过的空间就构成了一个完美的球面.仔细观察不难发现,有一条直径位置在旋转过程中一直保持不变,硬币外围的圆周是在绕着这个直径旋转,就得到了球面,这样就通过二维曲线旋转得到了三维曲面,将动与静充分结合.通过这个例子,学生们能自己归纳出旋转曲面的定义:一条平面曲线绕该平面上的一条定直线旋转一周所成的曲面称旋转曲面,平面曲线称旋转曲面的母线,定直线称旋转曲面的旋转轴[7].通过自己动手鼓励学生勤动手、勤思考,培养观察问题、分析问题、解决问题的能力.总结定义时要实事求是,遵循客观真理.由旋转曲面的生成方式,进而提出新的问题:旋转曲面的方程如何得到?
2.3 推导方程,归纳方法
下面讨论旋转曲面方程.为了方便,将旋转轴取作z轴,将母线所在的平面作为yOz坐标面建立空间直角坐标系,建立yOz坐标面上的已知曲线C:f(y,z)=0绕z轴旋转所生成的旋转曲面方程.



在得出这一结论的过程中,采用基于问题的教学方法,逐步促进学生解决问题,一步步引导学生严密地推导,展现了数学的逻辑美,提高学生的高阶性思维能力和数学素养;体会数学中蕴含的唯物辩证法,一步步引导学生探寻问题的主要矛盾以及矛盾的主要方面,寻求正确的推导思路,并总结出建立旋转曲面方程的一般方法.
2.4 学以实用,首尾呼应
联系实际,探究常见的旋转二次曲面的方程和图形,明确求解思路和方法,最终提高学生分析和解决实际问题的能力.并且在生活中寻找相关旋转二次曲面的模型,理论与实际统一.

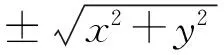
该旋转曲面称旋转单叶双曲面(图3),具有美观、稳定性好的特点,被广泛应用.通过课前布置的预习任务,学生们查找资料,学生们找到的这种曲面的模型有:火电厂冷却塔、广州塔小蛮腰等.旋转单叶双曲面属于直纹面,能够由一条条直线织成,称直母线.建筑物设计成这种曲面可以用直的钢梁建造,结构简单稳定又美观.
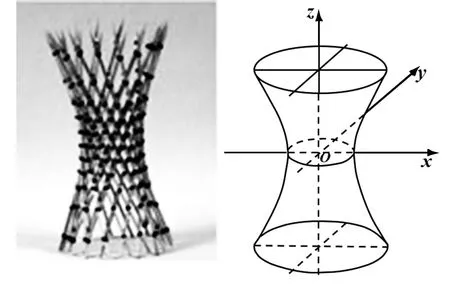
图3 旋转单叶双曲面
展示教具——竹签制作的旋转单叶双曲面模型(图3),讲解制作步骤,并按教学小组准备好材料,学生亲自动手,分组制作.不仅能加深对直纹面的理解,而且能培养动手能力、工匠精神与团结协作精神.接着让学生分组讨论,解决实际问题.
问题1灯笼是我国传统手工艺品,象征着团圆、喜庆,充满正能量,请问常见的灯笼是什么曲面?它可以如何生成?方程是什么?


图4 旋转椭球面
学生们分组讨论出旋转椭球面生活中的模型还有:大蒜、汉堡等.
问题2神州飞船返回舱的表面是什么旋转曲面?请问它可以如何生成?方程怎么写?
解是旋转抛物面(图5),可以由yOz坐标面上的抛物线y2=2pz(p>0)绕z轴旋转一周所生成,方程为:x2+y2=2pz.
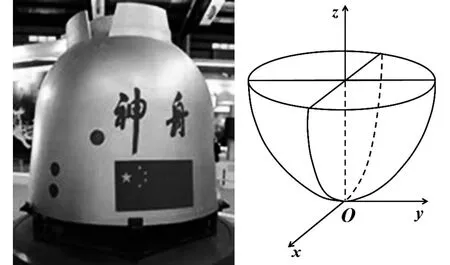
图5 旋转抛物面
学生们分组讨论出旋转抛物面生活中的模型还有:碗、锅、雨伞、灯罩等.
引导学生不但要抓住问题的本质,还要用发展的眼光看待数学知识的发展,也要用发展的观点看待或解决实际生活中的问题,学以致用.通过理论联系实际,学生不仅能欣赏到学习数学的方法美,而且能感受到数学理论与实际应用的融合美.
2.5 教学总结,落实育人
本次教学介绍旋转曲面,将抽象的数学知识与实际生活融合,学有所用,不仅使学生运用知识解决实际问题的能力得以提升,也能增强逻辑思维能力和数学素养.在教学的每个步骤中适当地融入思政元素,老师的旋转曲面素材展示了国人的智慧,同学们列举的旋转曲面素材许多与民族传统文化有关.中华优秀传统文化是我们最深厚的文化软实力,也是中国特色社会主义植根的文化沃土[5].
3 教学效果
本教学设计已经在江西师范大学高等数学课堂教学中进行了两轮实践,取得了良好的教学效果.授课结束时,利用智慧树在线平台的投票功能进行投票,学生对本次教学的满意度达到100%.从问卷调查结果来看,学生们对思政融入高等数学课程给予支持和肯定.

表1 本次教学满意度统计表
4 结 论
“才者,德之资也;德者,才之帅也”,本文通过具体的思政教学案例,帮助学生们实现德才兼备.课程思政对学生们的影响是近朱者赤的,故需努力从数学文化、数学家精神、数学应用、思维创新、数学辩证思想等方面挖掘思政元素,融入到每堂课的教学设计中.尽管高等数学课程思政研究已取得初步成效,但仍然任重道远.如何在教学过程中把数学学科知识体系与德育知识体系进行恰当的融合,是在高等数学课程中实施课程思政的难点[4].找到两种知识体系的相切点,将思政元素无形地融入数学课堂,合二为一,让学生在学习数学知识时不再感到晦涩,理解数学知识的来源,体会到学习数学的趣味性和实用性,更好地认识到不同学科的相互渗透[5].学生只有体会到了数学学习的趣味与实用,才能真正变要我学为我要学,从而进入数学学习的良性循环,真正达到育人的目的.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.
