基于K-means聚类和BP神经网络的电梯能耗实时监测方法

彭 诚

随着我国城镇化水平的不断提高，城市用地日趋紧张，为了提升土地利用率，城市中高层建筑数量急剧增长［1］.高层建筑中电梯需要长时间处于运行状态，上下运行与中间停靠耗电量较大，消耗较多能源［2］.巨大的电梯能耗已经成为当前人们关注的重点，为了降低电梯能耗，发展建筑节能技术，需要对电梯能耗进行有效的实时监测.

虽然现阶段全国建筑能耗监测平台已经运行了较长的时间，并获取了海量的电梯能耗数据；国内外相关领域的研究也取得较为显著的研究成果，但是目前的监管力度仍然不够深入.为了更好实现电梯能耗监测，吴城汀［3］提出基于Euclid范数的电梯能耗评价新方法，采用二次抛物线函数拟合电梯运行能耗与试验载荷的函数关系，对电梯运行工况进行分析.虽然该方法能够实现对电梯能耗的有效预测，但是对电梯能耗监测的精度较低，与实际能耗有一定误差.陈继文等［4］提出基于ARM的绿色建筑电梯能耗远程监测方法，实时采集电梯运行能耗数据，通过无线传输模块与STM32控制板进行实时通信，实现电梯能耗远程监测.虽然该方法能够为电梯能耗评估提供可靠的依据，但是对于电梯能耗的计算过程耗时较长，降低了实际的运行耗时.为了解决现有方法的不足，更好地实现现代建筑中电梯能耗的实时监测，本文基于K-means聚类算法和BP神经网络算法，提出一种新的电梯能耗实时监测方法.该方法先清洗能耗数据，提取影响建筑能耗特征值，然后利用相似系数法计算相似度，对相似电梯能耗数据进行小波分解，得到高低频序列.最后针对低频部分采用LSSVM-GSA检测方法处理，而高频部分采用均方加权处理方法，将两个结果重构，得到最终监测结果.仿真实验结果表明，所提方法能够有效提升监测精度，减少监测用时，同时能够保证监测过程的稳定性.

1 基于K-m eans聚类和BP神经网络的电梯能耗实时监测方法设计

1.1 电梯能耗数据清洗

由于电梯能耗数据之间关联性较强，所以无法单纯从任何角度出发证明随机一个能耗数据为异常数据，需要构建各数据之间的关联矩阵，对不同数据之间的关联进行深入分析.虽然BP神经网络的整体性能比较好，但是在样本数量较多且十分复杂的条件下，算法会出现计算速度慢、计算误差较大等问题.而K-means聚类算法能够针对各种不同类型的数据进行模块化分类，将相似度接近的数据集进行统计.由于数据的来源、种类不同，导致数据间的差异性也更大.为了进一步完善BP神经网络算法的性能，需在算法中加入K-means聚类算法.将聚类后的数据集作为BP神经网络的训练样本，使其能够获取更加准确的数据清洗结果，同时更好实现数据间的映射.研究结合上述两种算法对电梯能耗进行清洗，全面提升训练质量，其中电梯能耗数据清洗的具体操作流程如图1所示［5-6］.

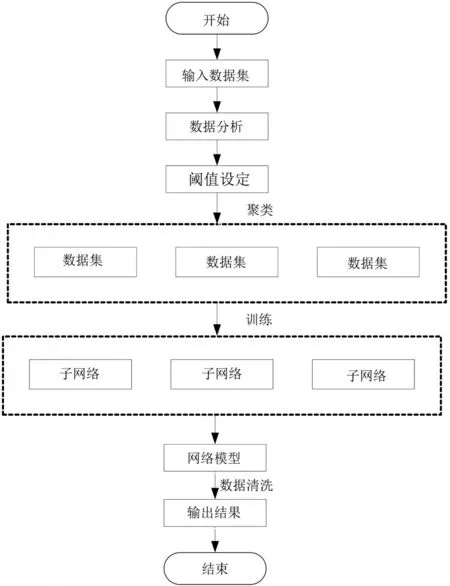
图1 电梯能耗数据清洗流程图

优先对不同类型的电梯能耗数据进行分类处理，结合分类结果进行阈值设定，确保最终聚类结果的准确性.将经过聚类处理后的样本设定为神经网络的训练样本，分析不同属性之间的关联性，构建属性间的映射关系，进而得到网络模型；将初始电梯能耗数据进行聚类处理，在对应的子网络模型中输入聚类处理后的数据，对其进行修正检测.

将物理或者抽象几何划分为相似对象的过程称为聚类，聚类属于一种无监督方法.Kmeans聚类方法主要用来解决经典的非线性划分问题.以下是通过K-means算法对样本进行分类的具体操作步骤.

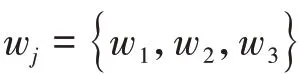
式中：n代表样本的维数，即样本归属和其相似度最高的集合.

当公式（1）成立，则样本xi所处样本集为wj，xi∈wj，通过阈值ε对样本集与聚类中心之间的相似度进行更新：

对数据集的聚类中心进行更新，则有：

式中：m代表样本集wj中的样本数量.如果满足公式中的条件，则停止聚类操作：

当对电梯能耗数据进行挖掘时，会出现部分性质相对比较特殊的数据，同时这部分数据的属性行为也十分不协调，会使数据逐渐转换为离群点.如果聚类算法初始聚类的选择是通过电梯能耗数据完成的，最终获取的数据中心可能会成为离群点，同时和实际聚类中心存在较远的距离.为此，当对不同类型的电梯能耗进行聚类处理时，需要优先对各个数据集的离群点进行分析.

针对各个连续变量而言，需要优先通过最小二乘法求解最小误差平方和最佳函数，同时进行匹配.另外，还需要引用最小二乘法对未知数据进行求解，确保最终求解结果和真实结果更加接近.因此采用最小二乘法拟合Sandia最终形成典型的电梯能耗年变化曲线，进而获取能耗的年变化规律.将两次获取的能耗值均方差设定为阈值，利用阈值对聚类中心的离群点进行检测，同时将离群点加入到对应的簇中.设定坐标系的横轴为时间，纵轴为能耗，经过绘制得到能耗的分布变化曲线.由于得到的曲线和正态分布相近，需要借助正态分布曲线估计方法进行计算分析，具体的计算式为：

式中：μ代表平均值；σ代表方差.利用f(x)函数进行对数选择，则能够获取式（6）的计算式：

令F(x)=Inf(x)，则有：

通过最小二乘法逼近F(x)，获取式（8）形式的方程组：

式中：a0、a1和a2代表方程组的参数.

其中，计算能耗的均方误差能够表示为：

BP神经网络是由输入层、隐藏层和输出层等组成［7-8］.各个层通过神经元连接，通过逐层连接，信息可以从输入层逐层传递到输出层，形成整个神经网络的运算过程.其中，网络训练主要划分为正向和反向两个步骤，具体的操作步骤如下：

①输入矩阵X进行归一化处理，则有：

式中：Xi代表归一化处理结果；min(X)代表输入矩阵的最小取值范围.

②误差正向计算.

设定网络中含有n个输入样本，第i个输入样本为xi.当xi输入到网络中，则输出的总误差计算式为：

式中：yi代表网络的实际输出；y*i代表网络的期望输出.

③通过反向传递进行权值修正.

设定随机两个神经元之间的连接权值为wq，求解总误差关于wq的梯度：

式中：W代表误差平均值.

在上述分析的基础上，将K-means算法和BP神经网络算法进行有效结合［9-10］，弥补两种算法的不足，实现样本训练，同时构建网络模型，获取不同数据源之间的映射关系，最终完成数据清洗.

1.2 电梯能耗实时监测

电梯能耗的变化和建筑内人员的活动存在密切关联，建筑内人员的活动会对电梯的能耗产生影响，使得电梯能耗会在一定周期内出现有规律的变化.高峰时段人员进出频繁，电梯的使用次数增加，从而导致电梯能耗上升；而在低谷时段，人员活动减少，电梯的使用次数减少，从而导致电梯能耗下降.其中，相似日的选择能够划分为两个部分，一部分是将能耗影响通过已经设计好的标准映射成对应的特征值，组建特征向量；另外一部分则是通过预测日相似程度确定相似日.设定存在n个样本日，同时各个样本日中都含有m个主导影响因素，则对应的特征向量能够表示为：

式中：xi(m)代表第m个影响因素的特征值.其中，第n个样本的特征向量矩阵可以表示为：

将任意两个特征的相似度标记为rij，则相似度矩阵能够表示为：

式中：R代表相似度矩阵.

在上述分析的基础上，构建电梯能耗实时监测模型［11-12］，具体的操作步骤如下所示：

①通过电梯能耗影响因素构建指标映射数据库，选取各个指标的映射标准值.

②通过相似度计算方法获取历史日和近似日的相似度，同时选择相似日.

③对步骤②中选取的相似日进行小波分解，获取高低频部分.

④通过LSSVM-GSA对低频部分进行监测，同时将全部输入和输出数据进行归一化处理.

⑤高频部分主要采取均方加权方法进行处理.

⑥将低频序列监测值和高频序列监测值进行小波重构，获取最终的监测结果.

2 仿真实验

为了验证所提电梯能耗实时监测方法的有效性，需要进行仿真实验测试.将文献［3］提出的基于Euclid范数的监测方法、文献［4］所提基于ARM的监测方法作为对比方法，与本文所提方法共同进行测试，以下为具体实验分析结果.

2.1 电梯能耗实时监测结果分析

实验选H城市的某SOHO区域作为研究对象，重点对2016年至2020年的该区域的电梯能耗监测结果进行分析研究.利用图2给出文献［3］方法、文献［4］方法和本文所提方法的电梯能耗监测值和实际值的对比结果，图3给出监测结果的精度变化情况.

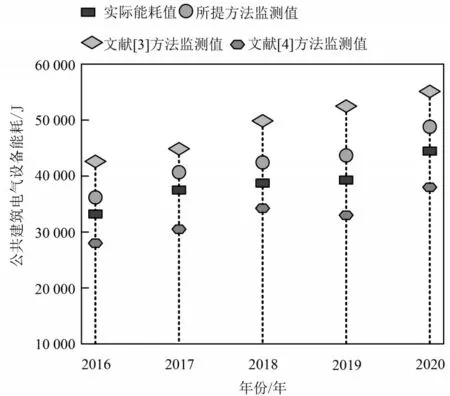
图2 不同方法的电梯能耗监测结果对比

图3 不同方法的电梯能耗监测精度对比结果

分析图2中的实验数据可知，三种方法的能耗监测值和真实能耗值存在不同程度的差异，但是相比另外两种方法，所提方法的电梯能耗监测值和真实结果更加接近.图3中的实验数据也更加全面地证实了所提方法的优越性，能够获取较为准确的监测结果.

2.2 监测用时分析

为了进一步验证所提方法的性能，在不同条件下，实验测试重点对比文献［3］方法、文献［4］方法和本文所提方法的监测用时，具体实验结果见表1.

表1 不同方法的监测用时对比结果

分析表1中的实验数据可知，由于测试对象和测试输入参数维度的不同，致使各个方法的监测用时存在十分明显的差异.但是相比另外两种方法，所提方法的监测用时明显更低一些，主要是因为所提方法在实际监测的过程中，增加了数据清洗环节，有效避免各种冗余数据导致监测用时增加.

2.3 监测稳定性分析

为了验证所提方法是否能够稳定运行，实验在均方根误差和最大相对误差绝对值不同的情况下进行稳定性测试，具体实验结果见图4和图5.

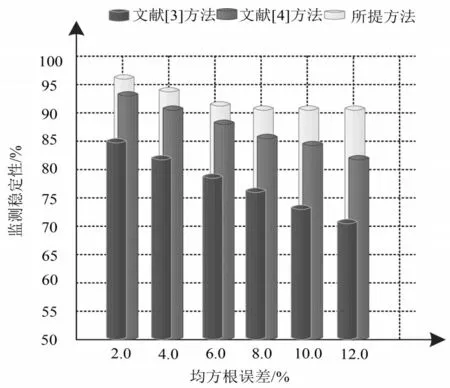
图4 不同均方根误差下各个方法的监测稳定性变化情况

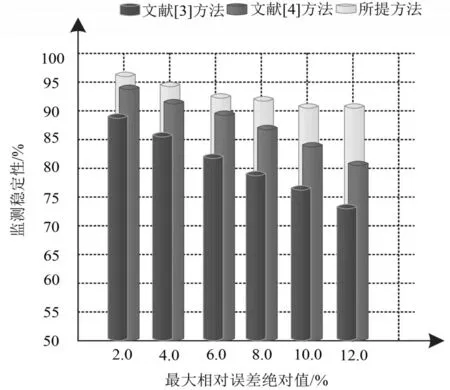
图5 不同最大相对误差绝对值下各个方法的监测稳定性变化情况

分析图4和图5中的实验数据可知，随着均方根误差和最大相对误差绝对值的增加，各个方法的监测稳定性呈下降趋势，但是相比另外两种方法，所提方法的下降趋势更加缓慢，监测稳定性更好一些.

3 结语

为了更好完成能耗监测，提出基于K-means聚类改进BP神经网络的电梯能耗实时监测方法，先对能耗数据进行清洗，提取影响建筑能耗的特征值.然后使用相似系数法计算相似度，并对相似电梯能耗数据进行小波分解以获取高低频序列，最后分别处理高低频数据，并将两者结果重构，得到最终的监测结果.仿真实验结果表明，所提方法能够有效提升监测精度，降低监测用时，同时获取更加稳定的监测结果.但是由于受到人为和外界因素的干扰，致使所提方法仍然存在一定的不足，后续将对其进行深入研究和完善.