一类广义Sylvester矩阵方程组对称解的MCG算法

陈世军

在控制与系统理论、图形恢复、信号处理等领域［1］经常会出现求解Sylvester矩阵方程问题，因此研究Sylvester矩阵方程约束解具有非常重要的实际意义和理论价值.近年来，许多学者研究了各类Sylvester矩阵方程，也建立了许多求解方程的算法.如针对连续的Sylvester矩阵方程AX+XB=F，李英［2］提出分裂迭代算法，将连续Sylvester矩阵方程的系数矩阵分裂为对称矩阵和反对称矩阵的分裂迭代算法，提高了算法的易操作性.顾传青等［3］给出了求解Sylvester方程的广义非对称PMHSS算法并分析了算法的性质.HU等［4］讨论了Sylvester矩阵方程的共轭迭代算法和Sylvester矩阵方程的最小二乘Hamiltonian解，对称矩阵在小波滤波器设计中有着非常重要的作用［5］.彭卓华等［6］基于共轭梯度算法，建立了一类求解矩阵方程组带有子矩阵约束的最小二乘对称解的迭代算法.

本文考虑一类广义Sylvester矩阵方程组的对称解，其矩阵方程组为：

式 中：Ai，Bi，Ci，Di，Fi∈Rn×n（i=1，2），X，Y∈Rn×n为未知矩阵.当Sylvester矩阵方程组有对称解时，建立MCG算法求该矩阵方程组的对称解，并在对称解集合中，求出给定矩阵的最佳逼近矩阵.

1 问题提出

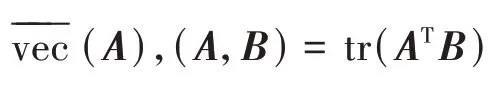
针对矩阵方程组（1）讨论以下两个问题.

问题1若方程组（1）有对称解，求(̂)∈SR，使得

2 求解问题1的MCG算法

先引入记号：

结合这些记号，基于共轭梯度算法原理，建立求解问题1的MCG算法步骤如下：

步骤1：任意给定矩阵(X1，Y1)∈SR，置k：=1，计算残差.

步骤2：更新矩阵.

步骤3：计算残差，更新迭代方向.

在迭代计算中，若在某次迭代出现R k=O，或者出现R k≠O而Q k=O时，则迭代终止.否则，令k：=k+1，迭代计算进入步骤2.很显然，在算法中得到的矩阵X k，Y k与P k都符合

下文给出MCG算法的基本性质，证明MCG算法在忽略舍入误差下能在有限步迭代计算后收敛.

性质1对任意的A∈Rn×n，(X，Y)∈SR，都有

证明 由矩阵迹的运算性质及X=XT，Y=YT，有

性质2对于MCG算法中的矩阵Ri，Qi和，有

性质3设k≥2，对MCG算法中的矩阵Ri和Qj，有

证明 因为

利用性质1和性质2可得

假设当k=s(s≥2)时，式（2）成立，则当k=s+1(s≥2)时，有

所以当k=s+1时，式（2）也成立.由数学归纳法原理可得，当1≤j＜i≤k时，式（2）成立.又由矩阵内积的性质可知性质3成立.

性质4设()∈SR是问题1的任意一组解，则任意给定一个初始矩阵(X1，Y1)∈SR，在MCG算法迭代计算中得到的矩阵R k，X k，Y k和Q k都满足

证明 当k=1时，有

假设当k=i(i≥2)时，式（3）成立，则当k=i+1时，有

由数学归纳法原理可得性质4成立.

定理1设问题1相容，对任意的初始矩阵(X1，Y1)∈SR，文中建立的MCG算法能在有限步迭代计算后收敛，也就是得到方程组（1）的一组对称解.

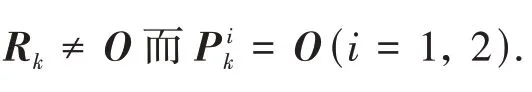
定理3假如问题1有对称解，那么任取矩阵H1，H2∈Rn×n，只要矩阵(X，Y)符合

则经过有限次迭代计算后，在MCG算法中可以得到方程组（1）的唯一极小范数对称解.

证明 结合文中建立的MCG算法和定理1，按照式（4）选择任意一个初始矩阵，那么经过有限次迭代计算后可得问题1的一组对称解，并且对称解矩阵形式为：

下文证明(X*，Y*)是问题1的极小范数对称解，考虑矩阵方程组

由上述分析可知，方程组（1）与方程组（6）是同解的，即问题1的对称解也是方程组（6）的对称解，这里把问题1的解集合记作SE，用来表示方程组（6）的解集合，则可得SE⊂.这里要证明问题1的极小范数对称解是(X*，Y*)，只需证明(X*，Y*)是方程组（6）的极小范数对称解.约定矩阵的乘积运算优先于矩阵的Kronecker积运算.

记

将式（5）中的矩阵X*，Y*按行拉直可得

3 求解问题2的MCG算法

当问题2有约束解时，其解集合SE为非空集合，取(X，Y)∈SE，有

由矩阵内积运算可得，上式等号右端两个矩阵的内积为零，因此

则求解问题2中给定矩阵的最佳逼近矩阵解等价于求矩阵方程组

4 数值算例

根据文中建立的MCG算法求解矩阵方程组（1）的对称解和极小范数对称解，以及求解给定矩阵X(0)，Y(0)∈Rn×n的最佳逼近矩阵，这里系数矩阵均为n阶方阵，当 ||A≤10-9时，则认定矩阵A为零矩阵.算例中的程序均在Matlab软件2014版-PⅣ3.0 GHz微机环境下运行，其中系数矩阵如下：

①若选择初始矩阵X1=Y1=I，根据文中MCG算法可得矩阵方程组（1）的一组对称解，其中计算时间（秒）、迭代次数、实际误差及解矩阵范数随着矩阵阶数n的变化如表1所示.

表1 方程组（1）对称解的计算结果

②在式（4）中取H1=D1，H2=D2作为初始矩阵，按照MCG算法可求得矩阵方程组（1）的极小范数对称解，当n=1时，求得矩阵方程组（1）的极小范数对称解为：

当矩阵阶数n增加时，得到的计算结果如表2所示.

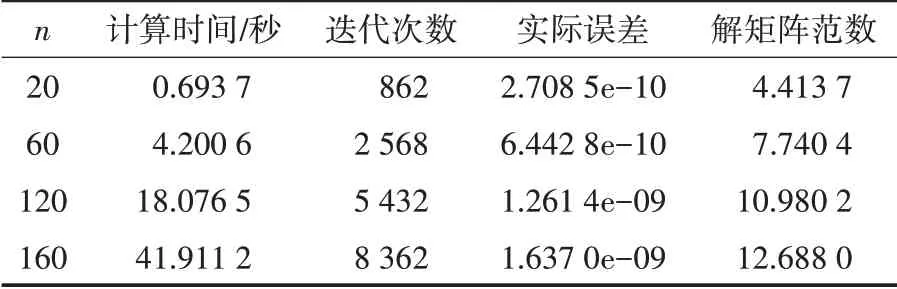
表2 方程组（1）极小范数对称解的计算结果

在SE中X(0)，Y(0)的最佳逼近矩阵为：

5 结语

文中基于共轭梯度算法原理建立了求解一类广义Sylvester矩阵方程组对称解的MCG算法，该MCG算法能自动判断方程组是否有对称解，同时MCG算法对方程组的系数矩阵不要求正定或者列满秩，因而被广泛应用于求解线性方程的各类约束解.若修改算法中的矩阵类型，还可以给出求Sylvester矩阵方程组其他约束解的修正共轭梯度算法.