GA-PCA模型在高校教育管理中的应用效果研究

郑 妮

随着我国高等教育的普及与发展，准确和有效利用学生成绩数据辅助教学管理和调整学生学习进程，已经成为高校教育管理的重要课题之一.已有研究大多基于传统的统计学方法进行学生成绩预测，忽略了学生成绩的模糊性和不确定性，难以得到有效的结果［1-3］.同时，高校教育系统中的各种原始数据复杂且高维，无形中增加了预测的难度［4-5］.因此，探索一种新型学生成绩预测模型十分重要.史耀凡等［6］通过构建PCA-GA-SVM模型对地表下沉系数进行预测，结果表明该模型具有较高的预测精度，能有效对地表下沉进行预测分析.乔守旭等［7］在研究数值下降的两相流流型中提出了PCA-GA-SVM预测模型，该模型对两相流流形预测具有较好的效果，在实际应用中具有一定可行性.施龙青等［8］为解决导水裂隙带发育高度的问题，提出一种PCA-GA-Elman优化模型，实验结果表明，该模型对高度预测具有较高的精度，能对导水裂隙带进行锁定.罗正亮等［9］在水电机组异常状态辨别中提出了一种基于PCA-GA-BP的神经网络，该模型能对水电机组的异常状态进行准确辨别，实现水电机组的实时性检测，随时防止危险的发生.经上述分析，GAPCA模型具有较好的优化效果.PCA能对数据进行降维，以提升整体模型性能.GA能帮助模型跳出局部循环，得到最佳解.因此借鉴已有研究，建立相关预测模型，旨在利用先进的计算方法对学生成绩进行更精确的预测.研究通过构建神经网络模型，使用GA和PCA对模型的前件参数进行优化.并通过PCA方法将复杂的多维数据进行压缩，提升模型的效率.另外，引入遗传算法对模型参数进行优化，提高模型的拟合性和预测精度.研究的创新点在于构建一个基于神经网络的学生成绩预测模型，此模型不仅考虑了学生成绩的模糊性和不确定性，而且通过引入遗传算法对网络的前件参数进行优化，提升了模型的拟合性和预测精度.

1 基于GA-PCA优化的学习预测模型构建

1.1 高校教育管理中学习预测模型的构建

在高校教育管理中，关注和提升学生成绩是十分重要的工作.当前，对学生学习成绩造成影响的因素较多，例如课程难度、教学方法、学生积极性等，学习预测模型能通过影响因素对未来成绩进行预估，在帮助学生进行状态调整的同时，促使教育管理部门提前采取干预措施，进行针对性教学［10-17］.因此，构建和完善学习预测模型对提升学习成绩和教育质量具有积极意义.研究在自适应神经模糊推理系统的基础上对主成分分析与遗传算法进行改进，得到一个基于GA-PCA的学习预测模型.研究构建预测模型的具体流程如图1所示.

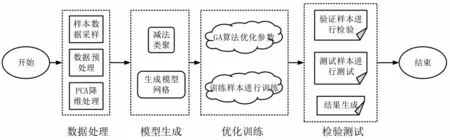
图1 学习预测模型构建的流程图

图1 中，研究采用主成分分析和遗传算法对模糊神经网络进行优化，主成分分析主要用于高维数据的降维，减少数据中的多余噪声，进而提升预测模型的运行效率和预测精度［18-20］.利用减法聚类方法与粒子群算法对模型和模型结构进行初始化，采用遗传算法对模型重要参数进行优化，解决模型陷入局部最优解的问题.在自适应模糊推理模型（ANFIS）中，一般有两项输入量，输入量用x与y表示；系统还包含一项输出量，用z表示.研究假设变量能划分为一大一小的模糊集合，对两条模糊规则进行定义，若输出量均为小模糊集合，则有公式（1）：

式中：f1表示偏小规则输出；p、q、r均为输入变量的权重系数，用于调整输入变量对输出结果的影响.同理，若输出量均为大模糊集合，则有公式（2）：

式中：f2表示偏大规则输出，系统的最终输出z由两项规则输出相加得到，则有公式（3）：

式中：w表示激活权重.在上述规则中，研究所构建的ANFIS模型如图2所示.

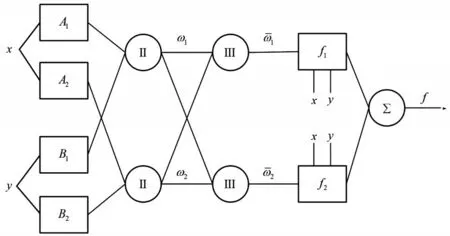
图2 ANFIS模型结构

图2中，A1、B1表示小模糊集，A2、B2表示大模糊集；ω表示隶属函数值的乘积.图中第一层为模糊化层，该层用于将输入变量进行模糊化操作.假设系统输入变量的隶属度函数为μA与μB，那么模型第一层的输出由公式（4）表示.

式中：O1表示隶属度值，而模型中隶属函数具有不同的形式.此次研究中，隶属函数如公式（5）所示：

式中：a、b、c均为提前参数，该参数值可通过学习算法进行调整.模型的第二层为强化层，该层表示所有模糊规则下的激发强度是通过隶属度叠加而成的，不能通过模型训练得到.隶属度的叠加如公式（6）所示：

模型的第三层为归一化层，该层将激励强度进行归一化，以便于不同维度数据进行比较，其归一化如公式（7）所示：

模型第四层是函数组层，该层的一个节点表示一个函数，该函数可视作规则下的输出值，并且函数呈线性函数，具有一定单调性，其输入量与函数参数成正比.第四层的隶属函数值如公式（8）所示：

模型第五层是模型的输出口，将前一层的输出结果累加，最后得到最终输出，其输出结果如公式（9）所示：

通过上述分析，研究选用的隶属函数决定了前提参数的形式，而规则的数量决定了结论参数的形式.

1.2 基于GA-PCA优化的学习预测模型

根据预测模型的构建流程，首先对样本数据进行PCA降维［21-23］.PCA降维能将多个特征压缩成少数典型特征.假设X为数据特征指标，则可用向量对特征进行表示，记作=(X1，X2，…，XP).对X→进行线性变换后，能得到一个新的向量，并记作.新向量的特征矩阵如公式（10）所示：

假设ai=(ai，1，ai，2，…，ai，p)，A=(a1，a2，…，ap)，能得到一定的约束条件.

约束条件1：ai=1.

约束条件2：在满足ai=1时，Y1的方差最大；当满足ai=1且与Y1没有关联时，Y2方差越大；以此循环能得到YP方差值.这些向量的排列顺序与方差大小具有一致的方向性.因此在选择向量时，一般选取靠前的向量.在预测模型生成的部分中，研究采用减法聚类的方法生成模糊神经网络结构.该方法在实际应用中具有一定的优势，可通过提供原始数据得到聚类中心点，之后采用排除法对非聚类中心进行删除.减法聚类方法是根据数据点附近的密度情况判别聚类中心与非聚类中心.假设在多维空间中存在一定数量的数据点，聚类中心则是这些数据点中的一个，此时数据点的密度值计算公式为：

式中：γa表示数据点的计算范围，即为聚类半径.根据公式（11）可知，聚类中心点周围具有越多数据，那么该中心点的密度值越大.在寻找第二个聚类中心点时，需要将第一个聚类中心的影响进行消除.假设选定的第一个聚类中心点为xc1，其密度值记作Dc1，那么第二个聚类中心点密度值如公式（12）所示：

根据公式（12）可得，第二个聚类中心若与第一个聚类中心的数据点进行比较，其密度值会显著减小，这样便可确定该数据点不属于相同聚类中心.在常规情况下，第二个聚类中心的半径大于第一个聚类中心的半径，这样可产生距离合适的聚类中心.在减法聚类方法中，产生初始的ANFIS模型，使该初始模型进行聚类优化，优化具体流程如图3所示.

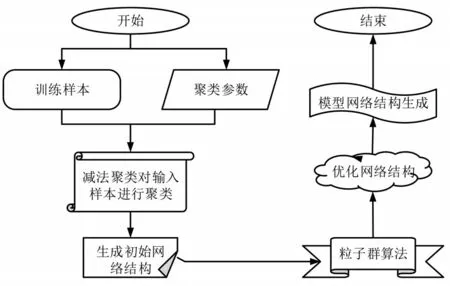
图3 减法聚类生成的ANFIS网络结构

在ANFIS中，其参数的调整通常利用混合算法完成.网络中的前件参数通过梯度下降法进行调整；网络中结论参数通过最小二乘法进行调整.这样的调整方式容易使模型陷入局部最优解，因此研究通过遗传算法对模型的前件参数进行优化.在遗传算法中，研究选取的编码方式为实数编码，将隶属度函数的中心与宽度作为遗传算法的种群个体；通过GA的适应度值计算对隶属度函数中心和宽度进行调整；GA的遗传操作中，研究采用轮盘算法选取最佳个体；在交叉操作中，研究选取单点交叉的方式增加种群丰富度；在变异操作中，确定个体基因的突变位置，然后根据随机变异概率对个体进行进化；将个体中最大适应度值作为模型的前件参数；设定模型的输出误差，并对模型进行训练.以上是基于GA-PCA的学习预测模型的全部构建过程.

2 基于GA-PCA的学习预测模型性能验证

研究采用MATLAB软件对构建的GAPCA-ANFIS模型进行仿真实验.实验首先利用主成分分析得到1 300组7维的学生成绩，并选取其中1 000组数据作为模型的数据集，其中训练集占比70%，剩余30%数据作为模型的测试集.使用训练集对GA-PCA-ANFIS预测模型进行训练，其结果如图4所示.

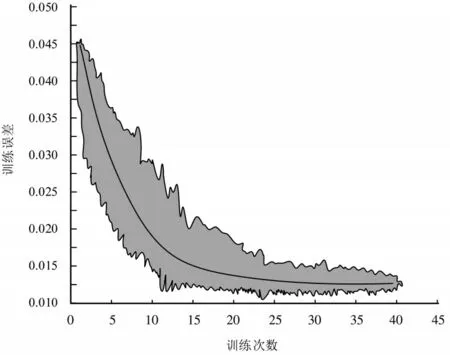
图4 GA-PCA-ANFIS模型的训练误差

图4 中，GA-PCA-ANFIS模型经过20次左右的迭代训练后，模型的训练误差从急剧下降变为逐渐趋于稳定，当模型经过40次左右的迭代训练后，模型的训练误差已稳定于0.011 9.实验结果表明模型经过训练，其误差会逐渐变小，并且训练误差未超出给定的误差值，表明该模型具有一定可行性.训练后的模型对学生成绩进行预测，其结果如图5所示.

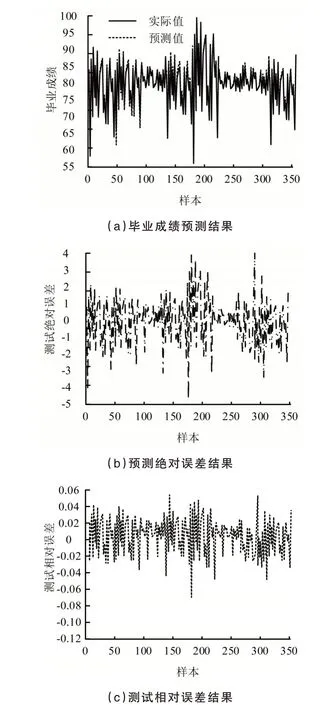
图5 模型的成绩预测结果

图5 （a）表示模型对学生成绩的预测结果，预测值曲线与实际值曲线基本处于吻合状态，该结果不仅说明模型在学生成绩预测方面的可行性，而且也提供了一种在实践中能准确预测学生成绩的方法，对于学生的学习进程管理和调整学习策略均具有重要意义.图5（b）表示模型预测结果的绝对误差，当样本数量在130左右时，模型正向绝对误差达到2；当样本数量在170左右时，模型负向绝对误差达到-4；模型绝对误差基本稳定在［-2，2］区间.图5（c）表示模型预测结果的相对误差，当样本数量达到170左右时，模型相对误差为-0.07；当样本数量为290左右时，模型相对误差为0.05；模型的相对误差稳定在［-0.03，0.03］区间.实验结果表明模型具有较小的预测误差，并且成绩预测值十分接近期望值，因此模型具有较好的拟合性.研究将改进后的模型与ANFIS模型进行性能对比，对比指标采用均方误差和平均相对误差，其结果如表1所示.

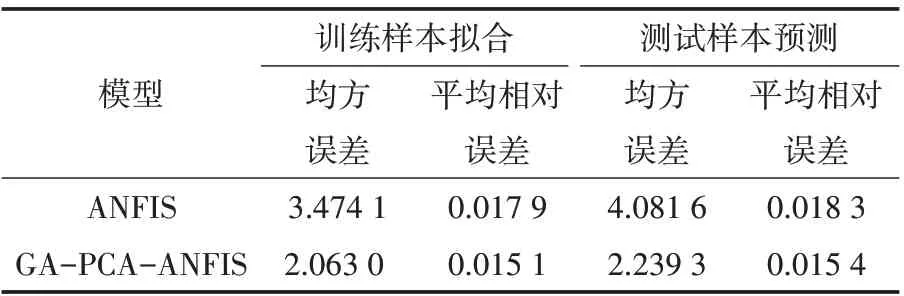
表1 模型性能对比结果

由表1可见，ANFIS模型训练拟合均方误差大小为3.474 1，平均相对误差为0.017 9；预测的均方误差为4.081 6，平均相对误差为0.018 3.上述数据表明，ANFIS聚类在训练过程中具有较好的拟合性，在预测过程中具有一定预测精度.但与GA-PCA-ANFIS相比较，改进模型的训练拟合均方误差为2.063 0，平均相对误差为0.015 1；预测的均方误差为2.239 3，平均相对误差为0.015 4，表明改进后的模型在拟合程度上与成绩预测精度上均明显高于ANFIS模型，因此所提出的GA-PCAANFIS预测模型能在高校学习管理中进行应用.

3 结语

研究针对高校管理中的学生成绩预测进行分析，构建了一个基于GA-PCA的学习预测模型.该模型是通过主成分分析与遗传算法进行优化的网络模型，通过PCA降维使高维数据向低维数据转变，提升模型的综合效率；使用减法聚类方法确定模型的聚类中心，得到最优ANFIS模型结构；最后采用遗传算法对网络的前件参数进行优化，从而得到全局最优解.研究通过仿真实验对模型进行验证，结果表明构建模型的训练误差仅为0.017 9，训练拟合均方误差为2.063 0，平均相对误差为0.015 1，预测均方误差为2.239 3，平均相对误差为0.015 4.实验结果证明研究提出的模型具有较好的拟合性和较高的学习成绩预测精度，同时该模型在高校管理中的实际应用效果较优.

研究仍存在不足之处，研究利用遗传算法对模糊神经网络的前件参数进行优化，而结论参数未进行改进，因此后续研究可从结论参数优化的角度出发，寻找一种更适合的算法进行优化.