渗流管涌作用下松散堆积层结构演化规律
2024-05-10蔡沛辰毛雪松胡仪喣解阔
蔡沛辰, 毛雪松, 胡仪喣, 解阔
(长安大学公路学院,西安 710064)
松散堆积层是第四纪形成的地质体[1-2],当路线穿越松散堆积层或路基采用松散堆积填料进行填筑时,易出现路基失稳、滑塌和不均匀沉降等典型病害[3],而这些病害又往往与松散堆积层强渗透性密切相关,究其本质常常是松散堆积层的渗流管涌问题。在渗流管涌发展过程中,水流冲刷会带动松散堆积层中土颗粒发生迁移[4],随冲刷时间的增加,其内部结构也将发生改变,进而出现“空洞”,引起路基稳定性和承载能力降低。因此,从颗粒流角度研究渗流管涌作用下松散堆积层内部结构演化规律至关重要。
目前,国内外众多学者针对管涌发展过程进行了大量研究[5-13]。理论研究方面,罗玉龙等[5]从潜蚀发生的几何条件、水力条件及潜蚀数学模型等3个方面详细总结了潜蚀研究的相关进展;沈辉[6]通过理论分析和推导,提出了以侵蚀颗粒流失与土体变形双向作用为耦合机制的多场流固耦合模型。试验研究方面,Rosenbrand[7]分别采用粒子图像测速仪、粒子跟踪的图像减法和计算机技术研究了土壤颗粒的侵蚀行为及作用机理;杨曦等[8]通过开展铁尾矿的渗透破坏试验,分析了细颗粒含量与结构影响下的铁尾矿渗透破坏模式;冯上鑫等[9]使用核磁共振技术研究了土石混合体的渗透破坏过程;谷敬云等[10]通过自制可视化试验装置开展了透明土的潜蚀试验,研究表明潜蚀的发生发展进程是不均衡的,一般沿试样内部薄弱位置发展,最终形成贯穿上下游的优势渗流路径,诱发土体结构破坏。数值研究方面,倪小东等[11]开展了不同水力梯度下深厚覆盖层侵蚀型管涌的数值模拟,揭示了水力梯度对侵蚀型管涌发生发展的影响;Hu等[12]采用流体力学和离散元耦合的方法,对间断级配的管涌型土和级配良好的土体分别进行了管涌侵蚀的微观和宏观研究;随后,王霜等[13]模拟了管涌发展不同阶段堤基内部渗流场分布,确定了管涌发展各阶段颗粒流失的区域和范围,表明管涌动态发展是土颗粒流失与土体渗流相互影响、相互耦合的过程。上述研究已取得丰硕成果,特别是试验研究已由隔着试验箱观测逐渐转向可视化研究[14],但由于管涌发展具有极大的不确定性,且受限于试验装置,目前仍存在无法精准捕捉颗粒间运移细节的问题,而数值模拟可以很好地弥补这点,从细观角度模拟管涌发展破坏的全过程,对探究岩土体结构演化规律尤为便利。此外,由于松散堆积层自身的特殊性,已有的管涌研究成果主要集中于堤坝工程,并不完全适用于松散堆积层散体材料,明确渗流管涌作用下松散堆积层填料的结构演化特征对预防此类地质材料管涌破坏发生十分亟须。
鉴于此,现基于颗粒-孔隙尺度流固耦合方法,分别构建密实、中密和疏松结构的松散堆积层模型,对其开展渗流管涌测试,从细观角度探讨渗流管涌发展过程中颗粒迁移特征、颗粒流失量、颗粒间接触力链演化和骨架变形等结构演化特征,以期揭示渗流管涌背后的松散堆积层结构演化规律。
1 数值模型构建
1.1 模型构建及参数确定
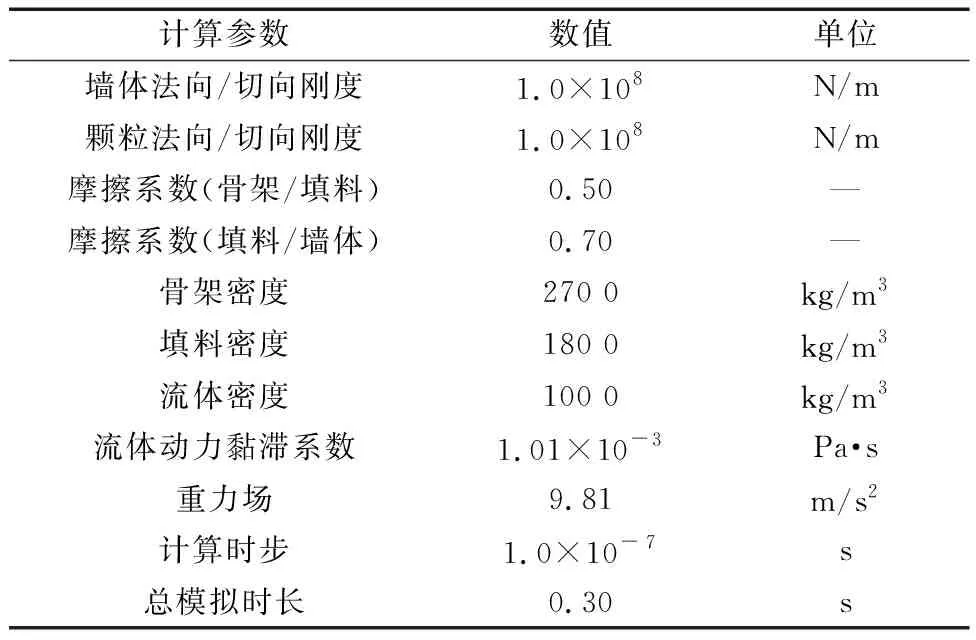
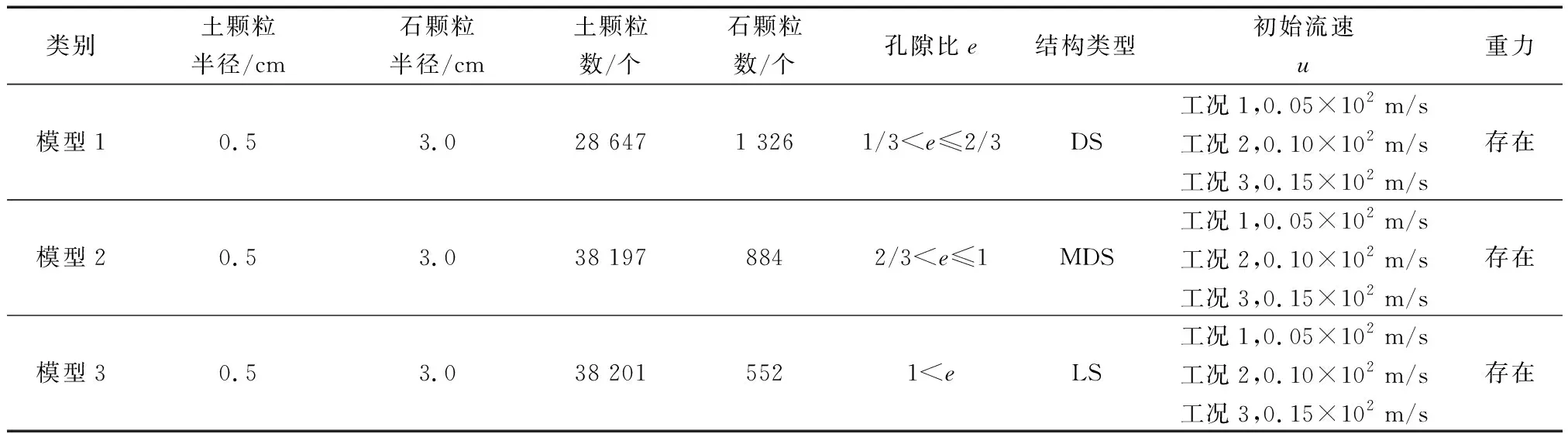
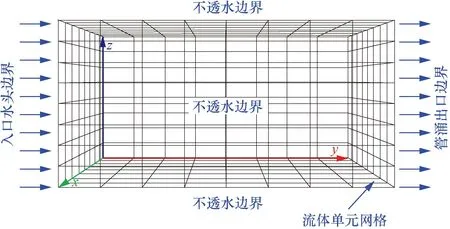
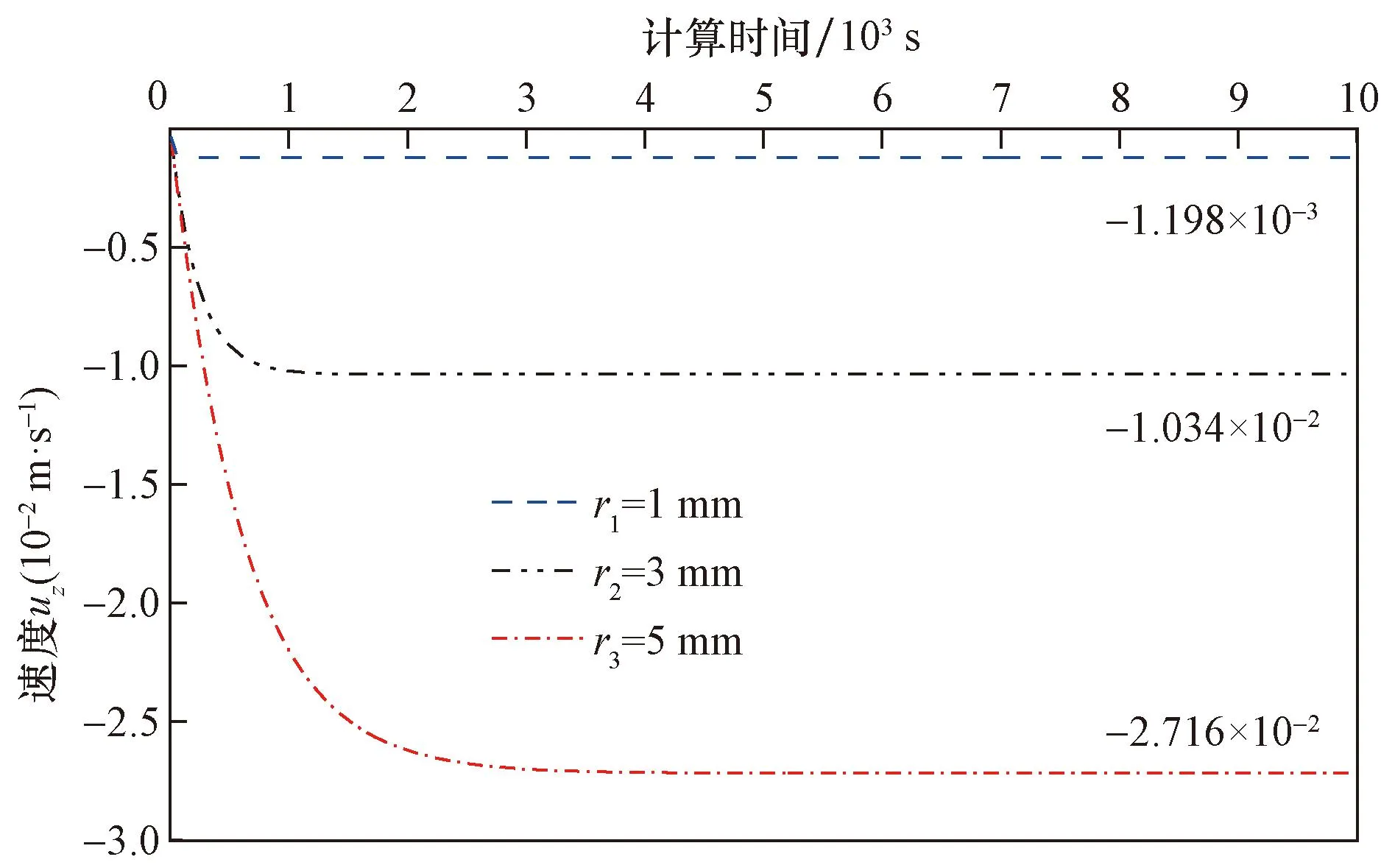
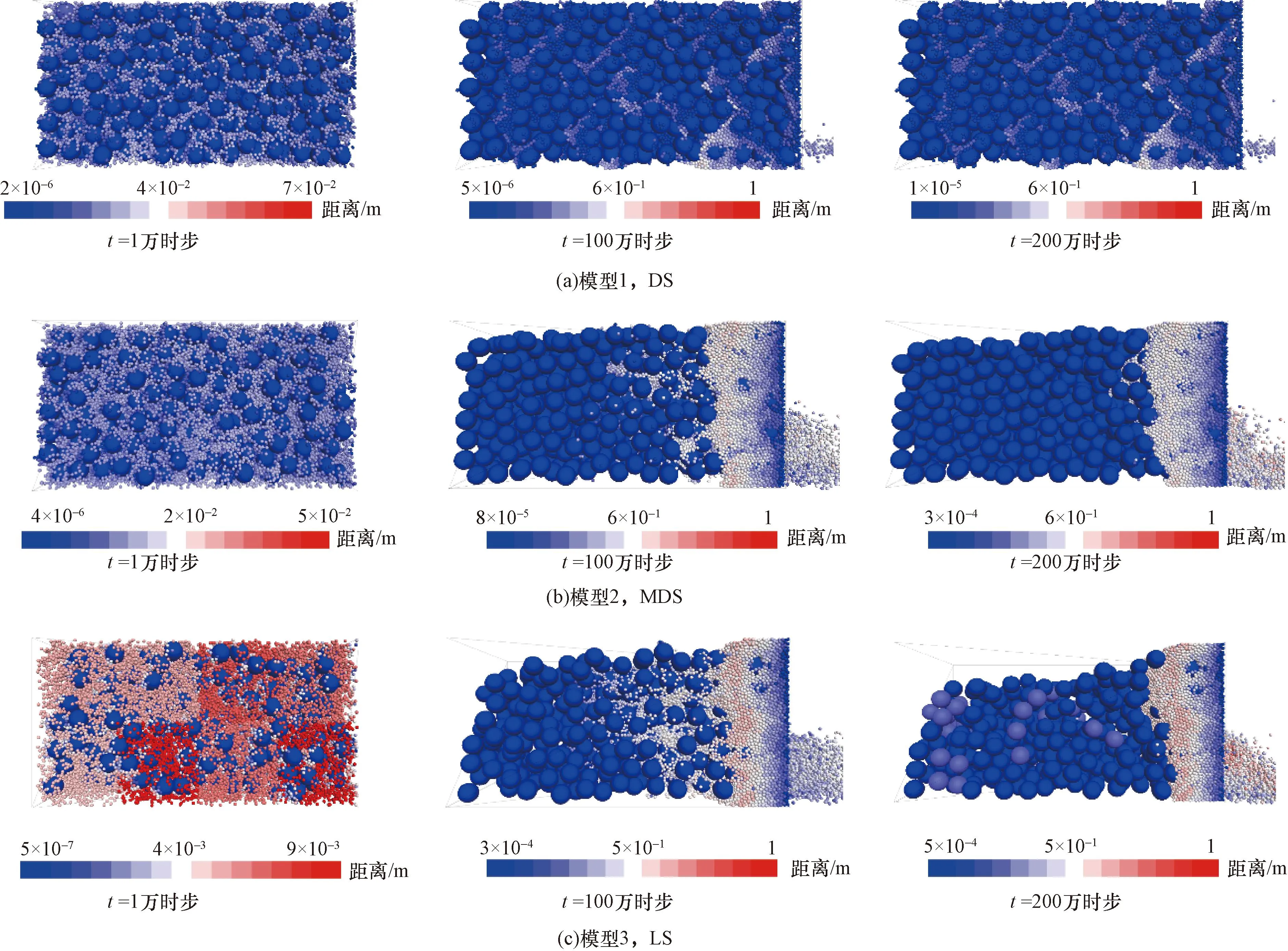
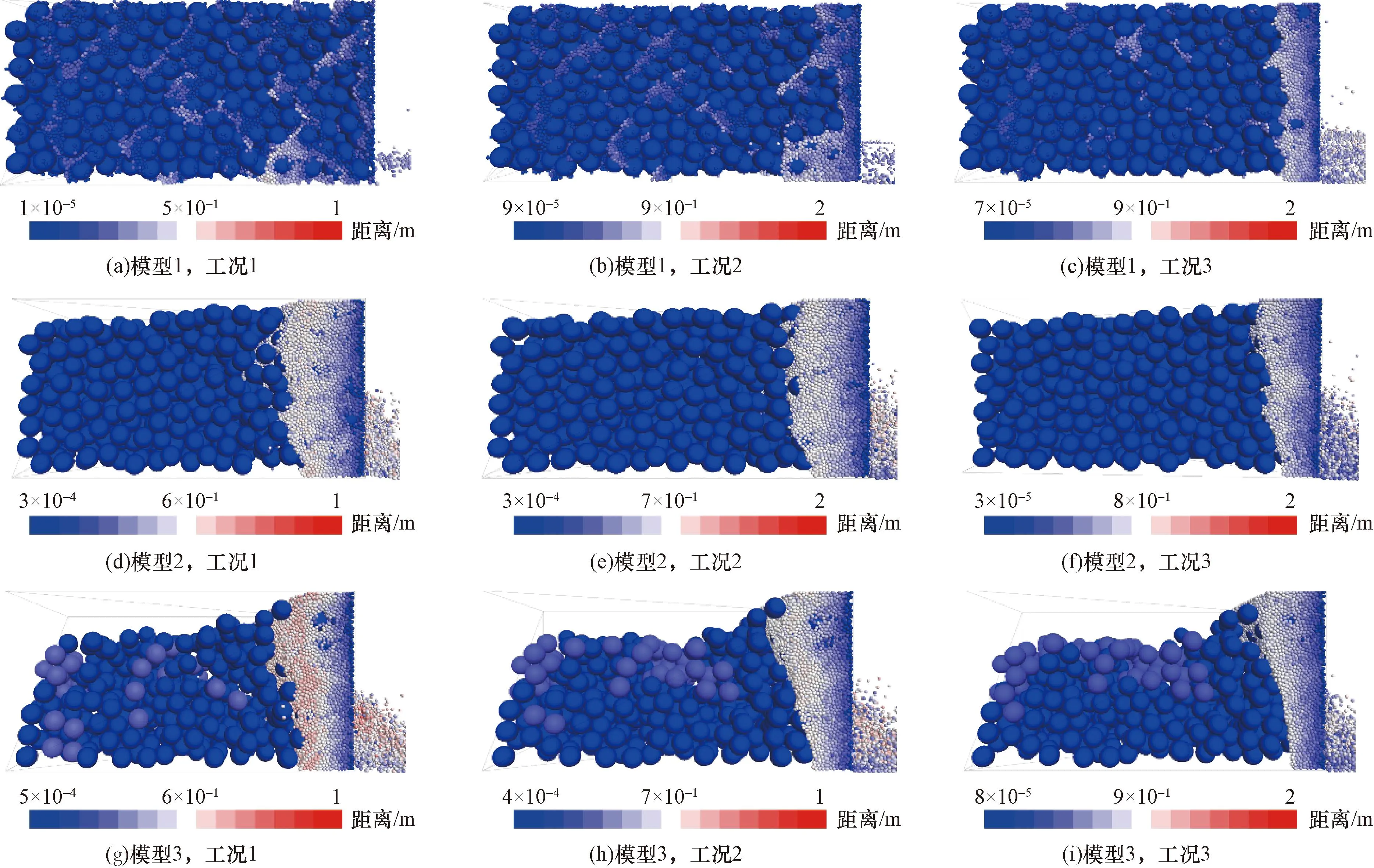
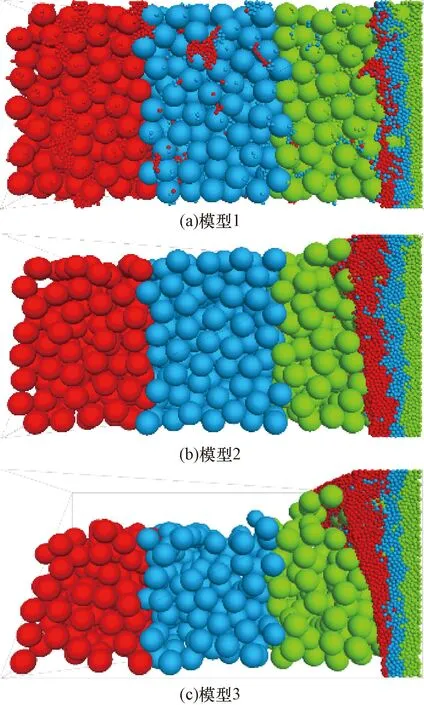
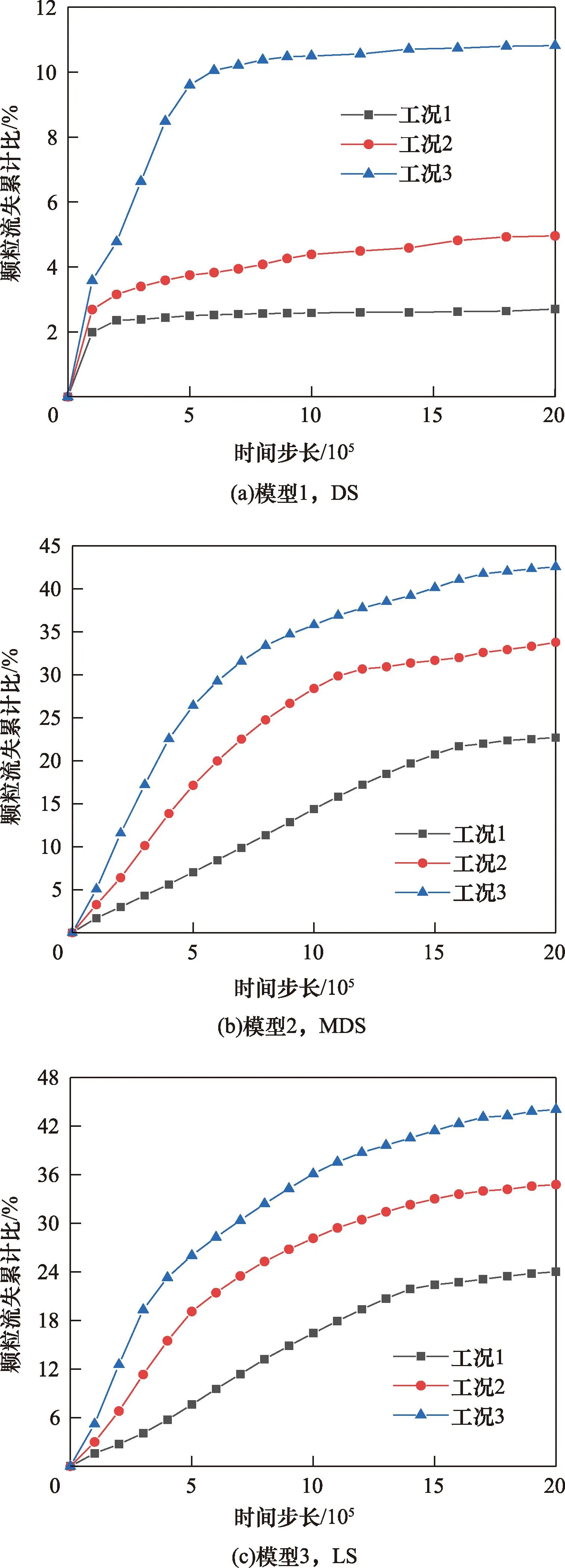
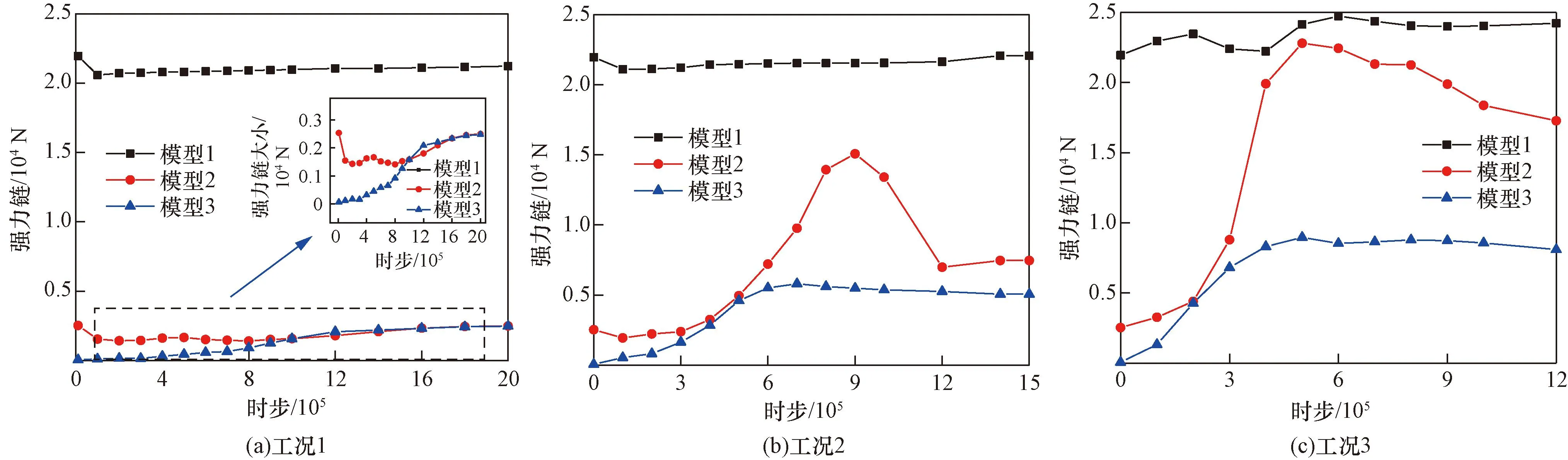
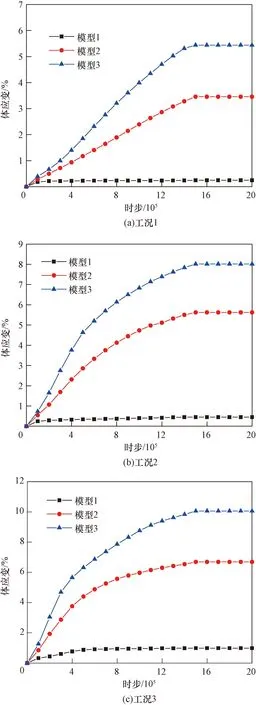
典型区域松散堆积层如图1所示,颗粒间的接触设置线性接触模型,并结合现场松散堆积填料实际情况和以往经验综合确定细观参数[3,11,14-17],如表1所示。考虑到松散堆积层材料的特点和模型构建的便捷性,参考Jin等[18]关于土石混合体的建模方法,将粗、细颗粒特征参数各参选含量较多且比较典型的块石和土颗粒为基准。基于此,参照表1和文献[3]的模型参数,采用“填充扩展法”建立了50 cm×50 cm×100 cm的松散堆积层数值模型,并以模型系统最大不平衡力小于1.0×10-5为平衡标准,即可认为颗粒处于自然堆积状态。模型疏密程度采用孔隙比e来表征,在文献[19]基础上,分别考虑密实结构(dense structure,DS,1/3 图1 松散堆积层现场图Fig.1 Site map of the loose accumulation layer 图2 松散堆积填料层模型Fig.2 Loose accumulation model 表1 细观计算参数Table 1 Mesoscopic calculation parameters 表2 侵蚀型管涌模拟工况参数Table 2 Parameters of erosive piping simulation conditions PFC3D(Particle flow code in 3 dimensions)中运用固定粗糙网格法对流体进行处理,将流体区域划分为若干流体单元网格,并确保所划分的流体网格中均包含一定数量的颗粒[20]。将整个模型沿长、宽、高分别划分为8、8、8份,单个流体单元网格尺寸为125 mm×6.25 mm×6.25 mm(图3)。此外,进行流体计算之前,需对边界条件进行设定,模型左侧设定为施加水头边界,上部、底部及侧壁均设定为不透水非滑移边界,入口边界与y=0 m平面重合,出口边界与y=1.0 m平面重合,渗流方向沿y轴正方向(图3)。最后建立5个测量球以监测和记录模型内部的孔隙率变化,测量球的球心位于模型槽的中轴上,圆心间距为125 mm,从左到右依次编号1~5(图4)。 图3 流体网格及计算边界条件Fig.3 Fluid grid and calculation boundary conditions 图4 测量球布设Fig.4 Layout of measuring ball 单颗粒在流体中的沉降是验证流-固耦合模型可行性最基本的方法[15,21]。参考试验研究可知土石混合填料渗流过程中土颗粒为主要迁移对象[4],故生成半径分别为1、3、5 mm的土颗粒进行验证,置于黏滞系数为1.50 Pa·s的流体中,在重力作用下,颗粒自由下落,其他相关参数如表2所示。 颗粒在重力作用下运动方程为 (1) 式(1)中:r为颗粒半径,m;g为重力加速度,m/s2;ρp为颗粒密度,kg/m3;ρf为流体密度,kg/m3;uz为竖向速度,m/s;t为沉降时间,s;Cd为阻力系数。 (2) 当雷诺数Rep较小时,阻力系数Cd为 (3) (4) 因此得到Stokes定律为 (5) 式(5)中:μf为黏滞系数,Pa·s。根据(5)式计算得到了3种不同颗粒的自由沉降速度分别为-1.163×10-3、-1.046×10-2和-2.906×10-2m/s。 通过DEM-CFD(discrete element method-computational fluid dynamics)计算获得了3种颗粒的沉降速度(图5),由于粒径不同,3种颗粒有不同的沉降速度,且最终达到一个稳定值,这是由于在自由下落过程中,重力与流体的拖拽力相互平衡。3个颗粒的最终沉降速度分别为-1.198×10-3、-1.034×10-2和-2.716×10-2m/s,这与Stokes定律计算得到的结果非常接近,误差介于1.15%~6.54%。因此可表明所建立的DEM-CFD流固耦合模型具有良好的可行性。 图5 不同颗粒沉降速度随时间变化曲线Fig.5 Curve of settling velocity of different particles with time 基于上述松散堆积层DEM建模方法和CFD模拟方法,可得到不同疏密程度下(DS,MDS和LS)松散堆积层的颗粒迁移位移演化图像,以工况3为例(图6)。由图6可知:随松散堆积层疏密程度的降低,颗粒迁移活动愈加剧烈(颗粒迁移距离越远),且随细颗粒流失量增加,松散堆积层骨架结构出现整体下沉态势,特别是LS模型尤为明显。此外,图7展示了不同初始流速下松散堆积层渗流管涌发展完成后的颗粒迁移状态。由图7可知,同一疏密程度下,初始流速越大,颗粒迁移距离越远,这也符合基本认识;同一工况下,松散堆积层渗流管涌破坏主要发生在LS模型,MDS和DS模型颗粒迁移量并不会直接造成松散堆积层骨架的破坏。 图6 不同疏密程度下松散堆积层颗粒迁移位移演化过程Fig.6 Evolution process of particle migration and displacement in loose accumulation layers under different density 图7 不同初始流速下松散堆积层颗粒迁移结果Fig.7 Results of particle migration in loose accumulation layers under different initial velocities 为便于直观查看颗粒迁移后的分布特征,沿y轴方向0~1/3、1/3~2/3和2/3~1.0 m区域进行分组,以展示不同疏密程度和初始流速下颗粒迁移后的组分分布特征(以工况3和模型3为例),结果如图8和图9所示。 图8 不同疏密程度下松散堆积层颗粒迁移分布特征Fig.8 Particle migration distribution characteristics in loose accumulation layers under different density 图9 不同初始流速下松散堆积层颗粒迁移分布特征Fig.9 Particle migration distribution characteristics in loose accumulation layers under different initial flow velocities 由图8和图9可知,松散堆积层渗流管涌发展过程主要以细颗粒迁移为主,局部区域存在“堵塞”现象,而块石颗粒仅会在细颗粒迁移脱空后,在重力作用下产生自由堆积运动。同时,颗粒迁移具有明显的颗粒堆积现象,堆积区域主要集中在出口边界处,呈“上多下少”的特点,随松散堆积层的疏松程度增加而愈加严重,但随初始流速的增加,有所缓解。以图9中模型3为例,计算堆积区域面积,工况1~3条件下的堆积面积依次为:s1=0.097 7 m2,s2=0.079 4 m2和s3=0.078 7 m2。分析其原因:颗粒迁移过程中,出口边界处由于渗流力及重力的共同作用,块石颗粒会优先向下堆积,而细颗粒相应会向上被挤压、迁移,故而造成其“上多下少”的颗粒堆积现象。此外,初始流速越大,颗粒流失量相应也越大,因此随初始流速增大,这种堆积效应会得到减弱。 图10统计了松散堆积层渗流管涌发展过程中颗粒流失量随时步的变化情况,可以看到,颗粒流失主要以细颗粒为主,系统达到稳定前,细颗粒流失保持着较高速率,表明渗流管涌的发生时间极短;随初始流速的增大,细颗粒流失量达到稳定的时间逐渐缩短,结构破坏进程加快;结合图6和图7可知,初始流速越大,颗粒流失总量越大,与倪小东等[11]研究结论存在差异,其原因在于粗颗粒与细颗粒粒径差达25 mm,而文献[11]中粗细颗粒粒径差仅为8 mm,粗颗粒形成的孔道势必不足以保证细颗粒有序通过,而研究中虽然也存在颗粒“堵塞”现象,但大部分细颗粒均能够有序通过孔道,不会造成严重的“堵塞”情况,这也与2.1节结论相一致。 图10 不同疏密程度下松散堆积层颗粒累计流失比随时步变化趋势Fig.10 Gradual variation trend of cumulative particle loss ratio in loose accumulation layers under different density 同时,图11展示了测量球区域内孔隙率随时步的变化趋势(以工况1为例),可以发现,当松散堆积层模型e> 1.0时,颗粒迁移过程中相同部位的孔隙率变化具有高度相似性,且随结构疏松程度越高,相应孔隙率变化越为剧烈。其中,模型1中各部位孔隙率均未随时步发生明显变化,这是由于其致密的结构特征所致。此外,从图11(b)和图11(c)中可知,5号测量球中的孔隙率呈先缓慢增加再减小,最后又平稳上升后趋于稳定,1~4号测量球均呈先上升后稳定的趋势,试样细颗粒的流失也主要体现在1~4号测量球中,约占测量球内颗粒流失总量的95%以上,5号测量球中的细颗粒由于有后续颗粒迁移的持续补充,故几乎没有损失。 图11 不同疏密程度下测量球区域孔隙率随时步变化趋势Fig.11 Gradual variation trend of porosity in the measurement sphere area under different density 力链是通过颗粒动力学模拟得到颗粒与颗粒间的接触状态和接触力,然后用线段把接触状态或接触力表示出来[22]。图12展示了同一工况下(工况3)不同疏密程度的松散堆积层渗流管涌发展前后的力链演化特征。由图12可知,模型结构越密实,强弱力链分布越均匀,渗流管涌发展后力链均发生不同程度变粗,最大接触力也得到提高,说明堆积填料内部应力传递结构发生了改变。其中MDS和LS模型渗流管涌发展前后,最大接触力分别由2×103N到1×104N、由6×101N到7×103N,分别提高了5倍和116倍,而DS模型最大接触力变化较小,说明DS堆积填料内部应力传递结构并未发生明显变化,结构较为稳定。同时结合图13强力链(最大接触力)大小随时步的变化关系可知,模型结构越密实,强力链数值越大,且随初始流速越大,强力链大小变化程度越剧烈,但其变化趋势较为相似。其中值得注意的是:初始流速较大的情况下,MDS强力链大小在工况2条件下90万时步和工况3条件下50万时步时均出现剧烈“跳动”现象,表明此时模型内部应力传递结构发生了较为明显的变化。 图12 不同疏密程度下松散堆积层渗流管涌发展前后力链演化特征Fig.12 Characteristics of force chain evolution before and after the development of seepage piping in loose accumulation layers under different density 图13 不同初始流速下强力链大小随时步变化趋势Fig.13 Change trend of the strength chain at any time under different initial velocity 图14为不同初始流速下接触数量随时步的变化趋势。由图14可知,渗流管涌发展的初始阶段,由于渗流力的施加,致使填料颗粒间接触数量陡增,特别是块石颗粒间接触承担主要的应力传递,其接触力增量较大。随着渗流管涌模拟的进行,土颗粒间、块石颗粒间以及土石颗粒间产生大量的接触力,相应的接触数量也将增加,且初始流速越大,新增接触越多,直至接触力链网趋于稳定时,接触总数也将趋于平稳,这点与细颗粒流失量累计占比随时步变化规律较为一致(图10)。 图14 不同初始流速下接触数量随时步变化趋势Fig.14 Change trend of contact number at any time step under different initial velocity 松散堆积层渗流管涌具有明显的“沉缩”现象,主要采用下沉量和体应变两个指标对其进行定量表征,以分析管涌发展前后的骨架变形特征。图15为不同疏密程度下松散堆积层模型下沉量随时步的变化趋势,由图15可知:试样下沉量随时步增加,呈先急剧下沉,后趋于平稳的态势,且初始流速越大,平稳时刻逐步提前,特别是模型结构越疏松,此特征越为明显。如LS模型中,在工况1~3条件下,下沉量的平稳时刻依次为160万,140万和60万时步。同时,结合图10可知,模型试样结构越疏松,颗粒累计流失比越大,以工况1为例,LS模型的颗粒累计流失比最大,MDS模型次之,DS模型最小,分别为24.02%,22.69%和2.69%,其规律与模型整体下沉量基本一致,这是由于随着试样结构密实程度的增大,填料孔隙率将变小,细颗粒越难以运移,进而模型试样整体骨架不会出现坍塌破坏,即不会出现较为明显的下沉量。 图15 不同疏密程度下松散堆积层下沉量随时步变化趋势Fig.15 Change trend of settlement depth with time step in loose accumulation layers under different density 此外,图16为不同初始流速下松散堆积层模型体应变随时步变化趋势。由图16可知,模型试样密实程度越大,渗流管涌发展后试样体应变越小,这均与上述模型下沉量和颗粒流失比关系相对应。同一工况下,模型试样3(LS)的体应变最大,依次为5.44%、8.01%和10.05%;模型试样2(MDS)的体应变次之,依次为3.45%、5.62%和6.69%,模型试样1(DS)的体应变最小,依次为0.24%、0.45%和0.98%。 图16 不同初始流速下松散堆积层的体应变随时步变化趋势Fig.16 Change trend of volumetric strain with time step in loose accumulation layers under different initial velocities 通过开展松散堆积层渗流管涌仿真试验,从细观层面分析了渗流管涌作用下松散堆积层颗粒迁移特征、颗粒流失量、颗粒间接触力链演化和骨架变形的结构演化特征。主要得到以下结论。 (1) 松散堆积层渗流管涌发展过程主要以细颗粒迁移为主,存在局部“堵塞”现象,而块石颗粒仅会在细颗粒迁移脱空后,在重力作用下产生自由堆积运动。颗粒迁移具有明显的颗粒堆积现象,堆积区域主要集中在出口边界处,呈“上多下少”的特点。 (2) 渗流管涌的发生时间极短,无明显破坏,但随初始速度增大,细颗粒流失量达到稳定的时间逐渐缩短,破坏加快。当e>1.0时,渗流管涌发展过程中相同部位的孔隙率变化具有高度相似性,且随着结构疏松程度越高,孔隙率变化越剧烈。 (3) 渗流管涌发展过程中,块石颗粒间接触承担主要的应力传递,力链演化的本质是堆积填料内部应力传递结构的改变。试样下沉量随时步的增加,呈先急剧下沉,后趋于平稳的态势,且随初始速度越大,平稳时刻逐步提前。 综上,组成支撑骨架的块石颗粒由于堆积咬合作用,并不会因水流冲刷产生明显迁移,而细粒则会在连通孔道中大规模迁移,导致结构改变,影响松散堆积层整体的稳定性和力学性能,特别是疏松结构填料层。

1.2 流体网格划分及监测单元设置

1.3 模型验证
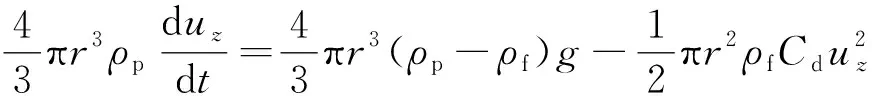
2 结果与分析
2.1 颗粒迁移特征分析
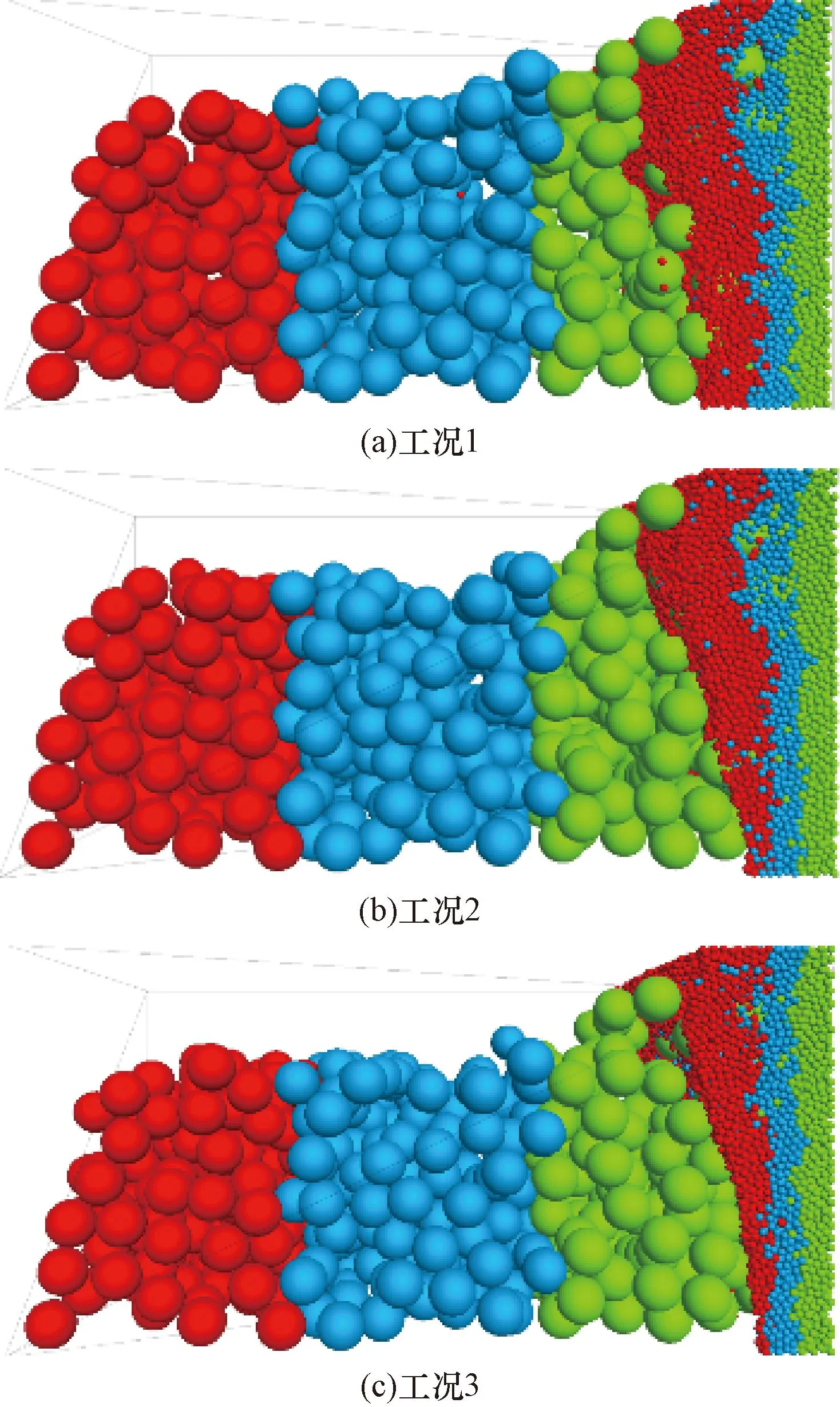
2.2 颗粒流失量分析
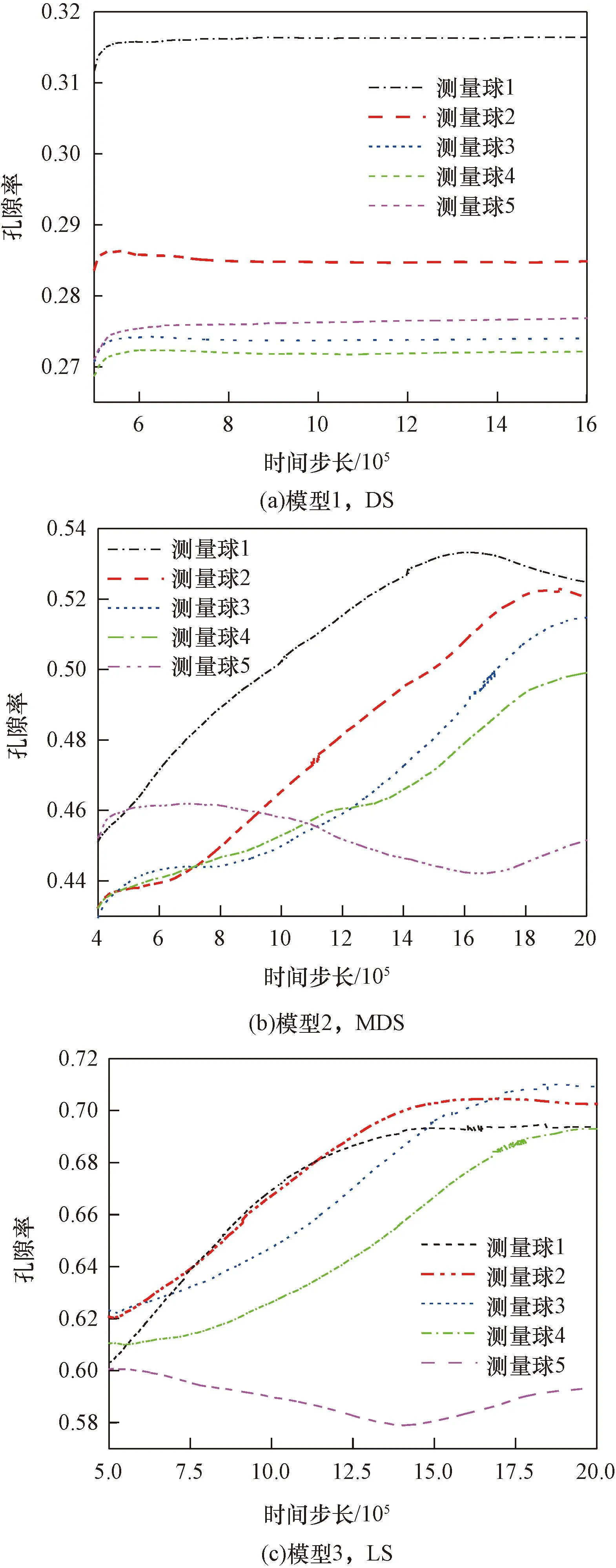
2.3 接触力链演化特征分析
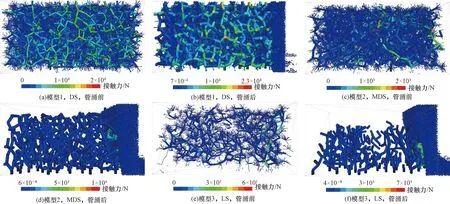

2.4 骨架变形特征分析

3 结论
