基于有限元与深度学习的大跨度桥梁智能设计方法

■付迎春 张 龙 范一娜 赵琼琳

（山东省交通规划设计院集团有限公司，济南 250000）

斜拉桥、 悬索桥等大跨度桥梁因其力学性能好、跨越能力强、外形美观而被广泛应用[1]。 此类桥梁大多应用于跨海等重要程度高的区域，也为结构的设计提出了更高的要求。 同时，大型桥梁结构需建立大量的设计参数和力学参数，为分析计算带来了较大的难度。 针对桥梁的设计，众多专家学者提出了可靠的设计方法和理念。 在桥梁结构的设计过程中，涉及大量的设计参数和力学参数，如何有效地融合这两类关键参数，实现结构的快速精准化分析是桥梁设计亟待解决的问题[2]。 本研究提出了基于有限元与深度学习的大跨桥梁智能设计方法，将有限元分析与神经网络融合得到了设计参数评估流程，进一步分析力学参数的可行性获取结构的合理设计参数，并以斜拉桥为研究对象，验证了本研究方法的可行性。

1 桥梁设计的基本原则

随着国家经济建设的不断发展，桥梁结构的建造技术也在不断提升。 其中斜拉桥、悬索桥等大跨度桥梁也在发挥着重要的作用。 大跨桥梁作为连接多地区经济、文化交流的交通枢纽，必须在结构设计的安全性和耐久性方面给予重视[3]。

1.1 结构影响因素分析

桥梁的设计与施工水平直接影响着使用阶段的舒适度，结构设计参数的选择是保证桥梁安全性和耐久性的关键。 影响桥梁工程结构的主要因素为构件的预应力不足、截面裂缝问题和耐久性考虑不充分，3 类因素对桥梁结构的影响见表1。

表1 3 类因素对桥梁结构的影响

1.2 结构可靠度设计

根据桥梁设计规范[4]，国内常用的耐久性分析方法为基于可靠度理论的极限状态方法。 在该方法中将影响结构可靠性的因素作为随机变量，统计结构所承受的各类荷载。 根据结构形式和材料特性计算结构的抗力，最终运用数理统计理论分析随机变量的特性，获取桥梁结构的总体可靠度。 据此可推导桥梁结构的失效方程，见式（1）。

公式中，Z（t）为结构的可靠性，R（t）为结构抗力随机过程；S（t）为结构荷载随机过程。

2 桥梁智能设计方法

依据桥梁设计的基本原则，要将设计参数与力学参数融合以保证结构在各类影响因素作用下的可靠性。 传统的设计方法通过有限元计算不同设计参数对应的力学参数，需要消耗大量的时间成本。 本研究将有限元计算与神经网络融合，有效降低了计算成本，同时也为类似的结构设计提供了参考。

2.1 有限元分析与深度学习的融合

在桥梁结构的设计过程中，根据有限元仿真的结果，提取设计参数与力学参数的对应关系，融合深度学习算法挖掘数据间的关联规则。 针对大跨桥梁结构的特点在结构的设计阶段形成设计参数与力学参数的关联机制，具体表述见式（2）。

公式中， f （a1，a2， …，am） 表示设计参数的集合体，a1，a2，…，am分别表示具体的设计参数，如拉索的尺寸、主梁的尺寸、拉索的间距等；g（b1，b2，…，bn）表示力学参数的集合体，b1，b2，…，bn分别表示具体的力学参数，如拉索的索力、应力、结构的位移等；⇔R表示根据结构的技术标准及数据关联规程则，不同设计参数与力学参数的对应关系。 在关联规则的驱动下可以实现对结构的智能化找形，通过改变设计参数获取结构的力学参数，判断结构模型的可行性。

本研究将有限元分析的结果形成样本集，输入神经网络中进行数据的智能化分析。 在有限元分析过程中形成设计参数与力学参数的关联样本。 以该样本为依据，将设计参数作为神经网络的输入层，将力学参数作为神经网络的输出层。 最终由力学参数评估设计的合理性。 有限元分析与深度学习的融合见图1。

图1 有限元分析与深度学习的融合

3 智能设计流程

本研究利用BP 神经网络进行参数关联规则的捕捉。 结构找形过程中，采用有限元软件进行仿真分析。 首先选择结构的设计参数，调整结构的找形工况，获取对应的力学参数。 结合结构技术规程，最终通过力学参数判断结构找形的可行性。 在本研究中，根据工程经验选取关键的设计参数及其具体的数值范围。 在有限元分析过程中形成大量的样本。样本中包含结构的设计参数和力学参数， 为基于BP 神经网络的结构智能找形模型的搭建提供了数据支撑。 根据大跨桥梁结构的特点，本研究中所选取的结构设计参数与力学参数的集合体具体表述为式（3）和式（4）。

公式中，DP 表示结构设计参数的集合，Ns表示拉索的间距，Ds表示斜拉索的直径，Rl表示桥梁的边跨中比，HL表示主梁的腹板长度，Bl表示主梁的翼缘长度，MP 表示结构力学参数的集合，Dp表示结构的竖向位移，σs表示拉索的应力设计参数的选择为仿真模型的搭建提供了基础，力学参数的选择为结构找形的可行性提供了依据。

根据BP 神经网络的架构和结构设计的特征，将各类设计参数归为神经网络的输入层，各类力学参数归为输出层。 通过有限元中设置设计参数与找形工况生成对应的力学参数。 将有限元分析得出的力学参数作为判断神经网络准确性的重要依据。 根据设计参数，输入模型中获取预测的力学参数。 通过对比两种途径获取的力学参数，不断调整预测模型的权重，最终形成高效可靠的找形预测模型。

4 案例应用

4.1 基本情况

在桥梁智能设计方法的驱动下，本研究以斜拉桥为分析对象进行了案例验证。 本研究所选取的斜拉钢索桥跨度为200 m，见图2。

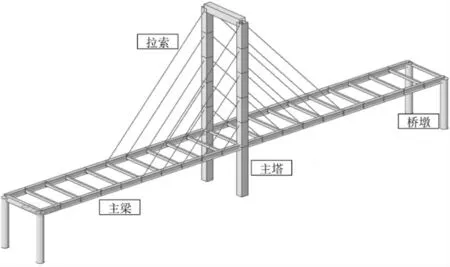
图2 斜拉钢索桥的结构形式

根据设计规范和本研究所提出的智能设计方法，在设计过程中，主要考虑的设计参数及其取值范围见表2，本研究重点考察结构的竖向位移是否超限，根据桥梁设计规范，最大位移的不得超过跨度的1/400。 根据式（1）计算最不利荷载工况下桥体的最大竖向位移。

表2 设计参数及其取值范围

4.2 结构受力性能预测

在有限元中进行设计参数的输入，并在荷载工况下获取结构的竖向位移。 有限元中设计参数与力学参数的计算见图3。根据位移云图可知，结构的最大竖向位移发生于边索与桥墩之间，应加强该部位的刚度。

图3 有限元中设计参数与力学参数的计算

根据设计参数的取值，在荷载作用下形成了大量的样本。 将设计参数与力学参数形成的关联样本作为数据集训练神经网络。 在训练找形预测模型过程中，当mse≤6.5×10-4时，模型停止迭代。 本研究分别探析了5 类设计参数对竖向位移的影响。 在训练后的神经网络中获取了不同设计参数对应的竖向位移值，同时在有限元模型中获取相同设计参数对应的力学参数。 部分样本中竖向位移的预测值与实际值的对比见图4。

图4 部分样本中竖向位移的预测值与实际值的对比

在分析过程中发现，本研究提出的设计方法具有较高的拟合度。 由于分析过程中将物理问题转化为数学问题，减少了边界条件设置、工况分析等步骤，显著降低了计算时间。 通过数据分析对比，本研究提出的智能设计方法在计算效率方面得到了显著提升。 处理相同数量的样本，对比有限元分析的时间（TE）和神经网络分析的时间（TM）获取计算时间的节省量（θ），见式（5）。

根据智能设计方法获取了保证结构位移不超限的设计参数集合。 拉索的间距为12 m，斜拉索的直径为150 mm，桥梁的边跨中比为0.8，主梁的腹板长度为2 000 mm，主梁的翼缘长度为2 000 mm。

4.3 参数化分析

本研究在神经网络的预测模型中进行了结构设计参数的分析，分别获取了多种设计参数取值下的力学响应。 根据表3 中5 种设计参数的取值，分析了各类参数对结构竖向位移的影响。 通过参数化分析可以有效获取提高结构安全性能的措施。

4.3.1 拉索的间距

根据规范要求，采用密距布置方案，拉索间距的取值范围是8～24 m。 在本研究中，控制其他设计参数不变，设置不同的拉索间距，竖向位移的变化见图5。由图5 可知，适当降低拉索的间距可以保证结构竖向位移不超过限制。 然而随着间距的降低，对竖向位移的影响明显降低。 因此，斜拉索的间距应保持在一定的范围内，过于密集对竖向位移的影响不明显且提高了建造成本。

图5 拉索间距对竖向位移的影响

4.3.2 拉索的直径

本研究拉索间距的取值范围是50～300 mm。 在本研究中，控制其他设计参数不变，设置不同的拉索直径，竖向位移的变化见图6。 由图6 可知，适当增加拉索的直径可以保证结构竖向位移不超过限制。 然而随着拉索直径的增加，对竖向位移的影响明显降低。 因此，斜拉索的直径应保持在一定的范围内，尺寸过大对竖向位移的影响不明显且提高了建造成本。

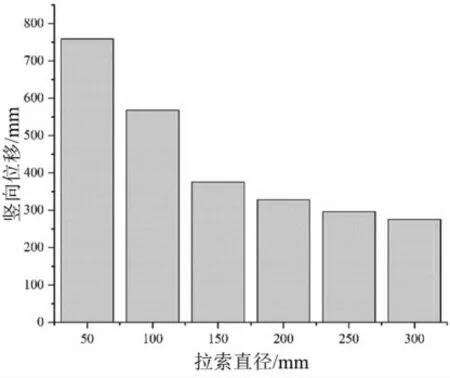
图6 拉索直径对竖向位移的影响

4.3.3 边跨中比

本研究边跨中比的取值范围是0.5～1.0。在本研究中，控制其他设计参数不变，设置不同的边跨中比，竖向位移的变化见图7。 由图7 可知，适当减小边跨中比可以保证结构竖向位移不超过限制。 然而随着边跨中比的减小， 对竖向位移的影响明显降低。 因此，边跨中比应保持在一定的范围内，比例过小对竖向位移的影响不明显且出现较长拉索提高了建造成本。

图7 边跨中比对竖向位移的影响

4.3.4 主梁截面

本研究主梁截面由腹板长度和翼缘宽度表示。在本研究中，控制其他设计参数不变，设置不同的主梁截面，竖向位移的变化见图8。 由图8 可知，主梁的截面提供了桥体的刚度，对竖向位移的影响最大。 因此，当桥梁变形超限时，增大主梁的截面尺寸是最有效的维护措施。

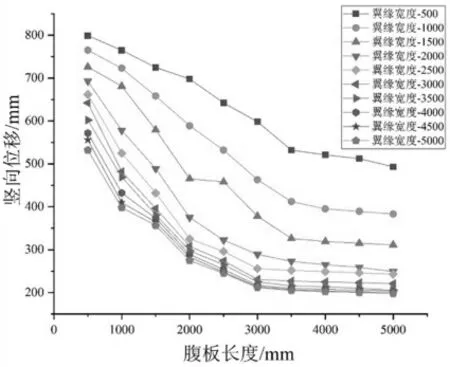
图8 主梁截面对竖向位移的影响

5 结论

大型桥梁的设计过程中，由于涉及众多构件和参数，存在着设计的效率低和精度不足的问题。 本研究提出了基于有限元与深度学习的大跨桥梁智能设计方法。 在研究过程中，明确了桥梁设计的基本原则，分析了结构性能的影响因素，并提出了结构耐久性设计的关键指标。 通过输入设计参数可以精准快速地获取结构的力学响应，为结构的设计提供了新思路。 本研究以斜拉桥的设计为例进行了研究方法的应用，所提出的智能设计方法相较于传统有限元方法效率得到显著提升，且具有较高的计算精度。