基于粒子群优化极限学习机的隧道地表沉降预测*

2024-05-08汪敏

施工技术(中英文) 2024年7期

汪敏

(中铁十八局集团第三工程有限公司,河北涿州 072750)

0 引言

在土木工程中,准确预测地表沉降对于提高建筑质量、避免发生事故、保障建筑物的安全稳定具有重要作用。对于地表沉降的预测研究也越来越多,洪英维[1]利用双曲线模型、指数模型和星野法模型分别对长三角地区某高速公路软土地表进行了沉降预测,发现这3种模型对于地表沉降预测均能起到较好的效果。聂珂珂[2]采用灰色理论模型对龙怀高速地表段沉降数据进行了预测,将智能算法引入传统沉降预测问题上,发现能较好地反映实际沉降规律。

随着人工智能的发展,机器学习方法在滑坡位移和地面沉降预测中得到了广泛的研究。极限学习机(extreme learning machine, ELM)是一种新型的神经网络学习算法,具有更好的学习能力,可以更好地用于沉降预测。但由于极限学习机模型的输入权重和隐藏层阈值是随机选择的,预测的稳定性不强,通过优化可以提高单个预测模型的性能算法。陈仁朋等[3]针对采用机器学习方法预测与控制盾构掘进地表沉降的研究,围绕预测模型输入参数、预测目标、预测算法和沉降控制4个关键环节的发展过程进行系统性地阐述。钟琛宜等[4]结合经验风险最小化和结构风险最小化原理,提出了一种改进的极限学习机回归算法,用于地铁沉降预测,发现该方法在地铁沉降中改进效果较好。粒子群算法(particle swarm optimization, PSO)是一种基于群体智能的全局随机搜索算法,可以有效优化极限学习机的相关参数。采用组合预测模型对地表沉降进行预测也成为机器学习领域预测方法的主流[5-7]。陈家骐等[8]运用粒子群算法对缓冲算子的可变权重以及新序列的初始值进行二维优化,从而提高DGM(1,1)模型的预测性能,该模型在隧道地表沉降预测中取得了较好的效果。何伟[9]为了提高隧道拱顶沉降的预测精度,引入了萤火虫优化算法对极限学习机的权值和阈值进行优化,提出了一种基于萤火虫算法优化的极限学习机预测模型,在地表沉降预测领域取得了较好的效果,但将粒子群算法和极限学习机结合用于地表沉降预测领域的研究较少。

本文利用粒子群算法对极限学习机预测模型进行改进,用粒子群算法的寻优特性,对极限学习机的输入权值和隐藏层阈值进行寻优,提高极限学习机预测性能。提出PSO-ELM预测模型,对济南轨道交通4号线燕山立交桥站地表沉降进行预测。

1 工程概况

1.1 项目概况

济南轨道交通4号线燕山立交桥东站位于经十路与燕山立交桥交叉口东侧,沿经十路东西向设置。车站南侧占据经十路辅路,车站北侧为窑头小区和中润国际城绿地。车站东西两端均接盾构区间,东、西端头均为盾构始发。

1.2 工程地质条件

根据现场地质钻探及附近水文地质资料表明,本区域地下水以碳酸盐岩裂隙岩溶水和构造裂隙水为主,局部存在第四纪松散岩类孔隙水。本次勘察期间揭露地下水稳定水位埋深10.4～15.7m,标高83.900～88.600m。通过搜集区域水文资料并进行现状水位调查,结合地形地貌、地下水的补径排条件,同时考虑地下结构与含水岩组的相互关系、大气降水的补给量大小、影响及工程的重要性(安全系数)和施工工况等因素,防渗设计水位按自然地面标高考虑。

1.3 现场监测

本文对济南轨道交通4号线一期工程盾构区间隧道地表沉降进行监测,在该盾构区间周边布置测点,监测其地表沉降情况,从2022年6月1日到2023年10月1日,每隔1天获取1个监测数据,测点布置包括周边建筑物、桥梁墩台或梁体、燕山立交桥东站D出入口。

本文以燕山立交桥东站D出入口周边的盾构区间监测情况为例,完成地表沉降监测分析。竖向位移监测可采用几何水准测量、全站仪三角高程测量、静力水准测量等方法,本项目采用几何水准测量法。

2 改进极限学习机模型构建

2.1 极限学习机模型

极限学习机是黄广斌教授在[10]2004年提出,ELM是一种单隐含层前馈神经网络算法。极限学习机的网络训练方式如图1所示。与常用的BP神经网络相比,极限学习机与BP神经网络不同,极限学习机只需要随机选择初始权重和阈值,并通过反向传播算法调整层间的权重和阈值即可以完成模型预测,极限学习机在随机选取方面大大减少了算法模型的学习时间,提高了模型的整体学习速度,降低了模型学习结构的复杂性,但同时由于随机选取的输入权值和隐藏层阈值也会导致模型预测结果不稳定,一定程度上降低模型的预测精度。

图1 极限学习机训练结构Fig.1 Training structure of extreme learning machine

极限学习机的输入层与隐含层间的连接权值及隐含层神经元的阈值在训练学习时随机产生,且在之后的网络训练过程中不再进行调整,主要通过设置隐含层神经元个数获得唯一最优解,典型的单隐含层前馈神经网络可表示为:

(1)

ωj=[ωj1,ωj2,…,ωjn]T

(2)

βj=[βj1,βj2,…,βjn]T

(3)

式中:ωj为输入层到隐含层第j个节点间的连接权值;βj为连接第j个隐含层节点到输出节点的输出权值;δj为第j个隐含层节点的阈值;αi为网络的输入;ωjαi为ωj和αi的内积;g(x)为激活函数;di为网络输出。

2.2 粒子群算法改进极限学习机预测模型

粒子群算法的基本原理起源于鸟群体在觅食过程中产生的行为研究。Eberhart和Kennedy提出了传统的经典粒子群算法,后经Shi对经典粒子群算法中的部分公式进行改进,形成了现在常用的标准PSO算法[11]。式(4)为标准PSO算法的速度迭代公式,粒子群算法的核心原理是在一定的空间中创造任意N个鸟群,即粒子。每个粒子在该空间中独立寻找对应的最优解,将这个最优解用于全部粒子群共享,从而实现优化过程。

(4)

引入标准的粒子群算法,将标准的粒子群算法用于对极限学习机的初始权值和隐藏层阈值进行寻优优化,从而构建PSO-ELM模型,用于燕山立交桥东站的地表沉降预测分析中,PSO-ELM模型的运行流程如图2所示。

图2 PSO-ELM 预测模型流程Fig.2 Flow of PSO-ELM prediction model

1)划分数据训练集和测试集、进行数据标准化处理,包括归一化和去异化处理。

2)确定极限学习机的网络结构。

3)生成粒子初始种群并设置粒子个数。

4)设置粒子群标准算法的相关参数、迭代次数和学习因子c1,c2。

5)保存并记录好当前迭代最优值。

6)判断误差是否小于给定误差,是否达到最大迭代次数,若是则停止迭代,执行步骤8),否则执行步骤7)。

7)根据式(5),(6)更新粒子位置和速度,返回步骤(6),执行迭代:

χk+1=χk+Vk+1

(5)

(6)

式中:ω为惯性权重;k为粒子群迭代数;V为粒子群速度;χ为粒子群位置;pbest为个体极值;gbest为群体极值;c1,c2为学习因子;r1,r2为[0,1]随机数。

8)确定极限学习机的最优权值和阈值,并进行网络训练。

9)使用改进的PSO-ELM预测模型对测试集进行预测。

3 工程案例验证分析

3.1 数据预处理

(7)

式中:α,β为归一化系数;dmax,dmin为样本中的最大沉降值和最小沉降值。

以燕山立交桥东站地表代表性断面过去两年沉降观测数据为研究对象,其地表沉降变化过程如图3所示。将监测数据进行时间分割,根据时间序列,利用前80%的数据为训练样本,进行PSO-ELM建模,对后20%的沉降数据进行预测。通过对前80%的数据进行训练学习,构建出PSO-ELM模型,利用训练得到的模型对后20%的数据进行预测,得到预测结果。

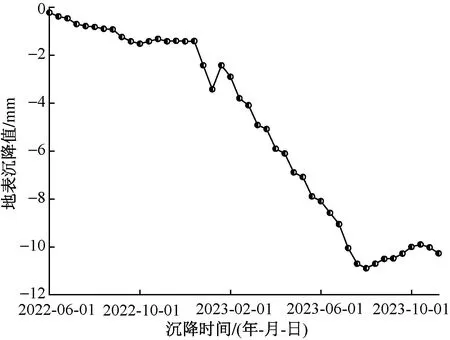
图3 地表沉降监测值Fig.3 Surface settlement monitoring value

本文选择了适合于极限学习机的Max-Min归一化方法。其主要过程是对原始序列进行线性变换,并将序列数据调整到[0,1]的范围内。对测点进行归一化处理,将初始监测沉降经过数据预处理后如图4所示。

图4 标准化后的地表沉降监测值Fig.4 Standardized surface settlement monitoring values

3.2 预测模型结果对比分析

利用标准化处理后的地表沉降值进行PSO-ELM算法训练,并输出预测结果。将PSO-ELM预测结果与传统的ELM预测结果进行对比,如图5所示。图5表现了前80%的训练结果与后20%的预测结果。由图5可知,PSO-ELM预测效果明显好于ELM预测效果,在传统的ELM预测中,存在波动的趋势,导致预测结果不稳定。经粒子群算法优化后的极限学习机模型能有效改进预测结果波动的不稳定性,提高了预测精度。

图5 地表沉降预测值Fig.5 Surface settlement prediction value

组合预测模型可通过均方误差(MSE)、均方根误差(RMSE)、平均相对误差绝对值(MAPE)3项指标来评定模型精度。MSE,RMSE和MAPE的值越小,预测效果越好。各精度评价指数的计算公式如下。

1)均方误差

(8)

2)均方根误差

(9)

3)平均相对误差

(10)

对PSO-ELM预测模型的结果和ELM预测模型的结果进行评价指标计算,计算结果如表1所示。由表2可知,相较于传统的极限学习机模型,经过粒子群算法改进的极限学习机模型MSE降低了22%,RMSE降低了28%,MAPE降低了5.3%。改进的极限学习机模型能够有效降低各评价指标值,各评价指标值越小,预测结果越好。

表1 模型评价指标Table 1 Evaluation index of model

表2 不同测点模型评价指标Table 2 Model evaluation index at different measurement points

传统的ELM预测的最终沉降量为10.22mm,而经粒子群算法改进的极限学习机模型预测的最终沉降量为10.14mm,与实际监测沉降量10.10mm仅仅只相差0.04mm,预测精度提高,说明了预测结果的有效性。

3.3 预测模型泛化能力分析

泛化能力是机器学习模型的一个重要性能指标,衡量模型在未见过数据上的表现。在进行泛化能力分析时,本文考察模型在训练集之外的数据上的性能表现,并探讨模型对新样本的适应能力。

本文对不同的隧道地表监测点样本分别采用ELM模型和PSO-ELM模型进行预测。对4个不同监测点的MSE,RMSE,MAPE 3个误差评价指标进行计算,结果如表2所示。

研究发现4个不同位置的监测点采用PSO-ELM模型的预测效果均较好。其中,监测点SD2和SD4都在盾构隧道掘进左线正上方的监测点,沉降变化趋势与监测点SD5相似,采用PSO-ELM模型预测的改进效果更明显。对于监测点SD4,相较传统的ELM预测模型降低了54.78%,改进效果最好。表2充分说明了PSO-ELM模型在不同空间位置盾构隧道地表沉降预测上的普遍适应性和泛化能力。同时验证了该模型能够普遍反映地表沉降变化趋势。