电网多源异构缺失数据最优投影整合算法研究

杨 晶,妥建军,李 昊,廖 翯,马雅蓉

(国网甘肃省电力公司发展事业部(经济技术研究院),甘肃 兰州 730046)

0 引言

随着智能电网的持续发展,电力数据量不断增加。电网大数据主要包括公共安全数据、在线监测数据[1-3]、调度运行数据和生产管理数据等。然而,由于这些基本数据的建模标准来源不同,导致数据类型存在差异,并且信息共享度较低,数据之间缺乏足够的交互。这一问题导致电网数据具有高度异构和多源等特征,给数据的管理和应用带来了巨大挑战[4-6]。为了有效监测和管理电网,有必要对电网多源异构数据进行整合。首先,数据的异构性导致数据结构和格式存在差异,需要作统一处理和标准化,以便数据的集成和分析。其次,不同数据源之间的信息共享度低导致数据的冗余存储和浪费,因而需要建立有效的数据交换和共享机制。此外,多源数据的整合还需解决数据质量和一致性的问题,包括数据异常值的检测和清洗,以及数据间关联性的建立和验证。为了解决上述问题,研究人员提出了包括数据挖掘、机器学习和人工智能等的一系列电网多源异构数据整合方法。这些方法可以通过对数据的预处理、特征提取和数据融合等步骤,实现对电网多源异构数据的整合分析和管理。同时,还需要考虑数据安全和隐私保护的问题,确保整合后的数据在使用和传输过程中不会泄漏敏感信息。电网多源异构数据的整合是实现电网智能化管理的重要步骤,需要综合运用各种技术手段解决数据的异构性、冗余性和安全性等问题。通过有效的整合和分析,可以更好地实现对电网的监测和管理,提高电力系统的可靠性、安全性和经济性。

近年来,很多学者针对多源异构数据进行了研究。莫慧凌等[7]根据张量Tucker分解理论,在无交互条件下建立高阶张量算法。该算法具有异构空间维度特性,可以提取数据的高维特征,故以此为依据可实现多源异构数据的整合。但是该算法无法消除多源异构数据中存在的噪声,且存在数据处理效果差的问题。赵春霞等[8]提出了一种基于极大元法和关联规则的数据挖掘方法,通过建立相异度数据结构矩阵来挖掘数据集中的最大频繁项。该方法利用平均加权法计算异构数据的特征,并通过高维相空间重构和时间反转处理,以实现多源异构数据的整合。然而,该方法在整合缺失数据时存在精度低的问题。张腾飞等[9]提出了一种基于粗糙模糊的K-means聚类算法。该算法考虑了类簇规模的不均衡程度,并引入自适应度量。通过对人工数据集和加州大学欧文分校(University of California Irrine,UCI)标准数据集的验证,证明了该算法的有效性。然而,该算法在数据处理方面可能存在误差。郭方方等[10]提出了一种基于有监督判别投影的网络安全数据降维算法。该算法利用近邻矩阵和类别标签信息构建有监督判别矩阵,并通过寻找最大全局散度矩阵和最小局部散度矩阵的低维投影子空间来实现降维。然而,该方法可能存在判别精度低的问题。

基于上述文献,本文提出一种针对电网多源异构缺失数据的最优投影整合算法。该算法创新性地引入拉格朗日差值方法填充缺失值,采用经验模态分解方法消除噪声,并建立投影指标函数将高维数据转换为一维投影值。该算法通过数据填充和去噪来提高电网多源异构数据的完整性和准确性,并利用混沌文化差分进化算法寻找最优投影方向,从而完成缺失数据的整合。该算法不仅具有较好的数据去噪效果,并且能够提高数据的整合精度和稳定性,有助于提升电网多源异构数据的质量和管理水平。

1 电网多源异构数据集中整合

1.1 野值数据修正与填充

传感器在电网中具有不同的采样周期,导致电网数据的时间存在不匹配的情况。网络延迟会对数据采集产生影响,导致整合中心与电网传感器之间的数据采集周期存在差异。为了提高数据整合的精度,需要对不同步的数据开展时间配准。在对电网多源异构数据开展配准之前,需要对数据中存在的野值进行检测。本文对阈值和修正值检测数据中存在的野值进行修正。修正后的结果v(k)为:

(1)

式中:rnew(k)为电网数据;C为野值判断参数;X(k)为第k个指标对应的修正值。

真实估计值对应的权重μ(k)可在v(k)的基础上通过加权函数获得。

μ(k)=el(k)v(k)

(2)

式中:l(k)为第k个指标加权函数;e为自然对数。

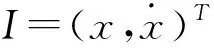
xi=Xn+TXn(i-n)+bi

(3)

式中:Xn为第n个测量序列;bi为电网多源异构数据中存在的噪声,dB。

传感器B采集的数据构成的测量向量En为:

(4)

式中:T′为数据整合时间,s。

通过上述过程完成电网数据的配准,获得高精度的电网多源异构数据。

为了确保电网多源数据密度的一致性,本文采用拉格朗日差值方法[13-14]填充电网时序数据,并采用拉格朗日差值函数F(t)填补电网时序数据tj。

(5)

式中:zj(t)为第j个差值基函数;ts为时序数据s对应的时间,s。

1.2 电网多源异构数据去噪

本文以修正与填充后的电网多源异构数据为基础。为了提高后续的集中整合质量,本文采用经验模态分解方法对多源异构数据作去噪处理。信号c(t)在电网多源异构数据中的功率Ax为:

(6)

式中:N为信号的数量,个。

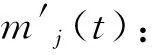
(7)

采用经验模态分解方法对电网多源异构数据进行去噪的具体过程如下。

①采用经验模态分解方法对含噪的电网多源异构数据信号c(t)展开分解,获得q个IMF分量。

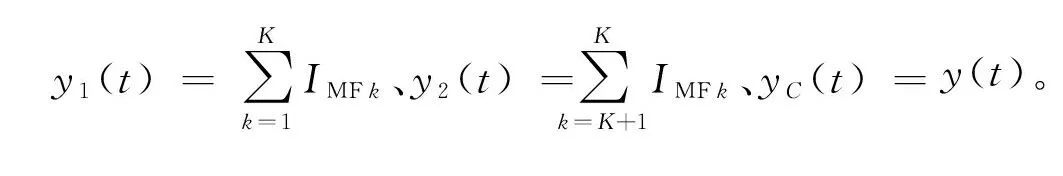
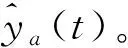
1.3 多源异构数据集中整合算法设计

对完成滤波处理的电网多源异构数据开展集中整合的具体过程如下。

①采用式(8)标准化处理预处理后的电网多源异构数据Cj={c1j,c2j,…,cMj}。

(8)

式中:cimax、cimin为数据i对应的最大值和最小值;rij为标准化处理后的数据。

②建立投影指标函数WF(a)。

(9)

式中:F(y)为两个样本点在每扇窗内的距离;D(y)为样本投影值对应的标准差;R(y)为单位阶跃函数。

根据投影指标函数WF(a),即可建立电网多源异构数据的聚类中心。

③高维电网多源异构数据经过投影处理后转变为一维的投影值。此时,维度M=1,存在权重w=1。电网多源异构数据的聚类中心dh和隶属度uhj为:

(10)

式中:rj为数据对应的特征值;c为电网多源异构数据种类的数量,个。

④模糊聚类迭代适应度G(uhj,dh)为:

(11)

如果适应度符合min{G(uhj,dh)}条件,则执行步骤⑤;否则,采用混沌文化差分进化算法搜索电网多源异构数据的最优聚类中心,并返回步骤③。

⑤利用混沌文化差分进化算法寻找电网多源异构数据的最优投影方向。

⑥通过式(12)计算电网多源异构数据的连续性类别特征值V(j):

(12)

式中:h为电网多源异构数据的类别。

根据式(12)计算结果对电网多源异构数据排序,获得数据的聚类结果,从而完成电网多源异构数据的整合。

采用迭代模糊聚类算法集中整合的电网多源异构缺失数据最优投影整合算法流程如图1所示。

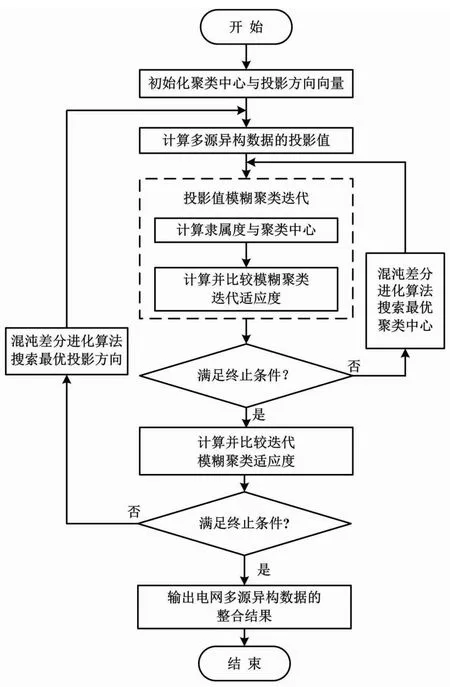
图1 电网多源异构缺失数据最优投影整合算法流程图

2 试验与分析

为了验证本文算法的整体有效性,需要对该算法进行测试。电网多源异构数据在采集过程中受多种因素的影响,导致数据中存在噪声,影响数据的整合效果。

含噪电网多源异构数据如图2所示。

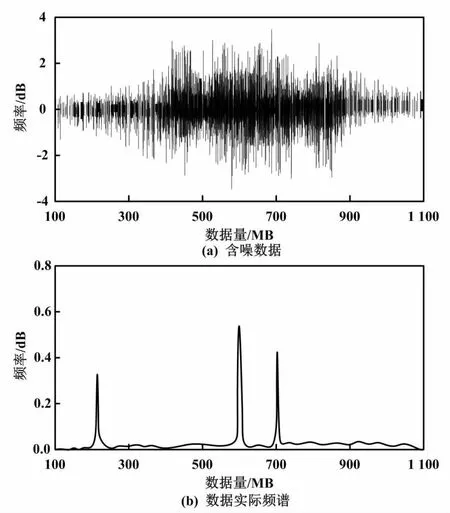
图2 含噪电网多源异构数据

本文采用本文算法、张量Tucker分解整合算法(文献[7]算法)、平均加权整合算法(文献[8]算法)对图2所示的含噪电网多源异构数据作去噪处理。

本文算法的降噪处理结果如图3所示。

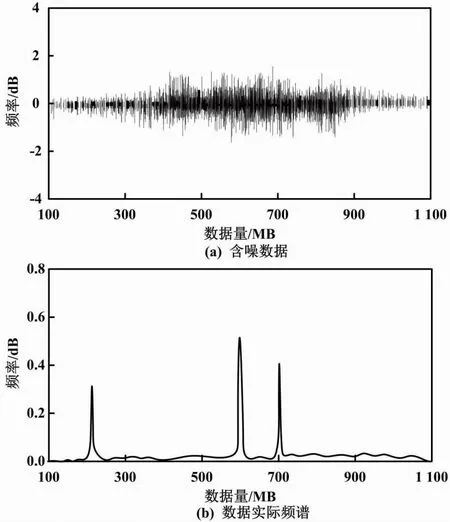
图3 本文算法的降噪处理结果

文献[7]算法的降噪处理结果如图4所示。

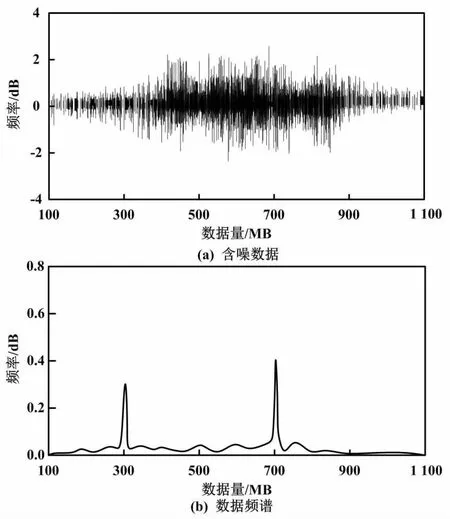
图4 文献[7]算法的降噪处理结果

文献[8]算法的降噪处理结果如图5所示。

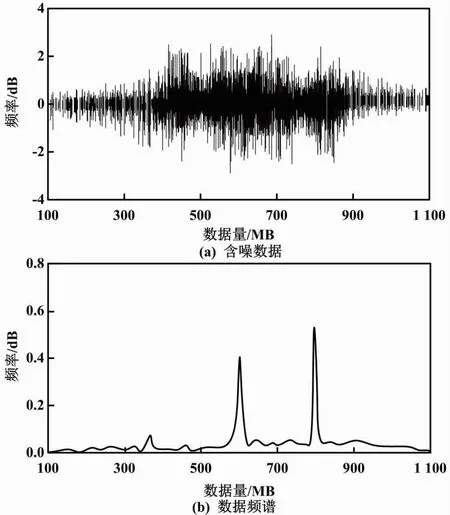
图5 文献[8]算法的降噪处理结果

由图3～图5可知,采用本文算法进行去噪处理后,含噪数据的波动频率明显降低,而文献[7]算法与文献[8]算法经降噪处理后,含噪数据的波动频率仍然保持较高的水平。这说明本文算法去噪效果较好。观察三种算法去噪后的数据频谱可以看出,相较于原始频谱,文献[7]算法与文献[8]算法去噪后数据频谱与原始频谱相差较大。这说明两种对比算法的降噪处理出现了一定程度的失真。而本文算法的去噪频谱与原始频率基本一致,说明本文算法并不会出现失真的情况,可以确保电网数据的完整性。

电网多源异构数据量较为庞大,对算法的时间复杂度提出了更高的要求,即要求整合算法能够在较短的时间内处理大量的缺失数据。因此,本文以时间复杂度为指标,将本文算法、文献[7]算法、文献[8]算法进行对比验证。

不同算法的时间复杂度对比结果如表1所示。

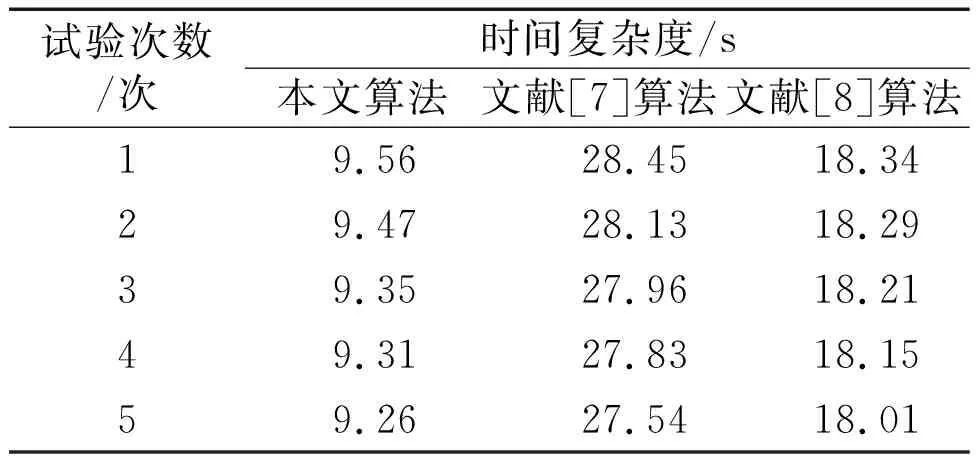
表1 不同算法的时间复杂度对比结果

由表1可知,随着试验次数的增加,三种算法的时间复杂度出现了明显的差距。其中:本文算法的时间复杂度最高未超过10 s;文献[7]算法的时间复杂度是三种算法中最高的,达到28.45 s;文献[8]算法的时间复杂度也高于本文算法,基本在18 s左右。这说明本文算法的时间复杂度明显下降,数据整合的效率提高。

算法在开展数据整合的过程中,其稳定性不可忽略。稳定性越强,则实际应用的可靠性越高。

不同算法的整合精度结果如图6所示。

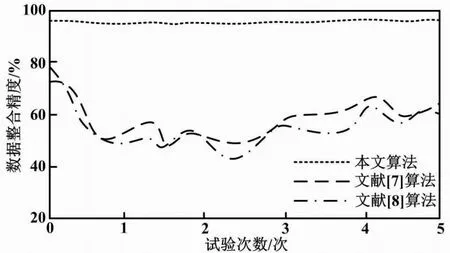
图6 不同算法的整合精度结果

由图6可知,三种算法中,本文算法的数据整合精度最高,且随着试验次数的增加,并未出现明显的波动。这说明该算法可以在提高数据整合精度的同时,确保自身运算的稳定性。观察两种对比算法可以看出,两种对比算法的数据整合精度最高均未超过80%,并且波动范围较大。这说明两种对比算法的稳定性略低于本文算法。

算法的收敛性指算法能否在迭代时间趋于无穷的假设下,找到问题的全局最优解。收敛性作为算法能否使用的关键性能,直观地体现了算法的可用性。因此,本文对三种算法的收敛性进行验证。

不同算法的收敛性结果如图7所示。

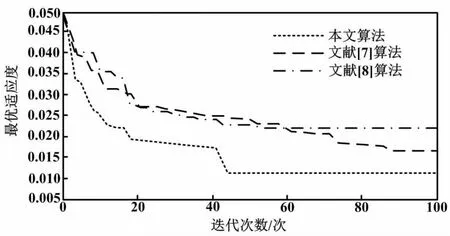
图7 不同算法的收敛性结果

由图7可知,本文算法在三种算法中收敛速度最快,且最优适应度值最低。文献[8]算法的前期虽然收敛较快,但是最优适应度值较高。由此说明本文算法的收敛性较好。

3 结论

针对目前电网多源异构数据整合方法中存在的数据处理效果差、整合精度低的问题,本文提出针对电网多源异构缺失数据的最优投影整合算法。该算法对数据开展了修正、填补和去噪处理,并在此基础上通过迭代模糊聚类算法实现电网多源异构数据的集中整合。测试结果表明,本文算法可有效消除数据中存在的噪声,并且可以确保去噪后电网多源异构数据的质量,以避免出现失真情况。本文算法的整合精度、稳定性以及收敛性均优于其他对比算法,整合精度始终稳定在95%左右。